Кинетические уравнения реакций различных порядков

1. Реакции первого порядка.

К этим реакциям относятся реакции изомеризации, термического разложения веществ, реакции радиоактивного распада и многие бимолекулярные реакции при условии, что концентрация одного из реагирующих веществ поддерживается постоянной.

Для реакции типа А → В скорость выражается уравнением:

V = - = К * С_А(2.15)

Или разделив переменные

- = К *и проинтегрировав данное уравнение, получим:

- ln C_A = K * τ + const

Значение constможно определить из начальных условий. При τ = 0 концентрация вещества А в данный момент (С_А) будет равна концентрации вещества А в начальный момент времени (С_О,А). Следовательно,const= -lnC_О,AВ этом случае

- lnC_A = К * τ -lnC_О,А

Или

- lnC_A +lnC_О,А= К * τ

Из полученного выражения

К = (2.16)

Это уравнение называется уравнением реакции первого порядка. Оно дает возможность вычислить концентрацию реагирующего вещества в любой момент времени по известной величине константы скорости или, наоборот, найти константу скорости реакции при заданной температуре путем определения концентрации в любой момент времени.

Если через Сх обозначить уменьшение концентрации исходного вещества к моменту времени τ, то уравнению можно придать вид:

К = 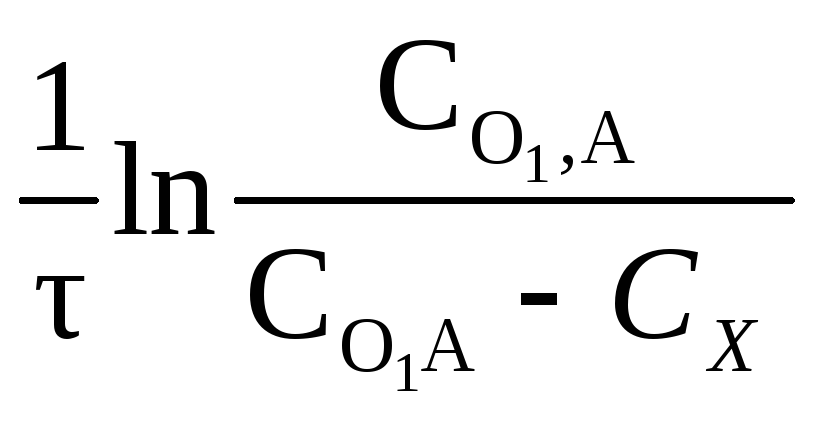(2.17)

Для характеристики скорости реакции первого порядка наряду с константой скорости часто пользуются величиной, называемой периодом полураспада (τ^1/2), то есть временем, необходимым для того, чтобы прореагировало половина взятого вещества. Принимая, из уравнения (2.16) находим:

К = 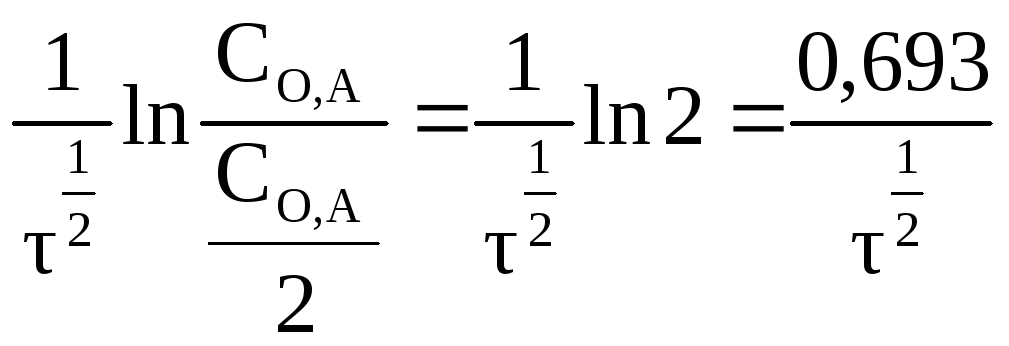или= 0,693/К (2.18)

Из уравнения видно, что время полураспада для реакции первого порядка не зависит от количества вещества.

Следует также отметить, что константа скорости в уравнениях первого порядка имеет размерность обратного времени [K] = С^-1, мин^-1

2. Реакции второго порядка.

К ним принадлежит большинство бимолекулярных реакций и некоторые тримолекулярные. Реакции второго порядка можно представить схемой А + В → продукты реакции.

Скорость такой реакции определяется уравнением:

V = - = К * С_А* С_В

Где С_{А и} С_В– концентрации реагирующих веществ в момент времени τ.

Рассмотрим простейший случай, когда концентрации двух реагирующих веществ одинаковы, тогда

- = К * С²(2.20)

Разделить переменные и проинтегрировав уравнение

(С^-2* dc =) получим

const (2.21)

При τ = 0, С = Со, const = , тогда-= Кτ или

К = (-) =() (2.22)

Заменив С на С_о- С_х, получим:

К = () =() (2.23)

При условии С_А≠ С_Вуравнение скорости реакции в дифференциальной форме имеет вид:

- = К * С_А* С_В= К (С_О,А- С_Х)(С_О,В - С_Х)

Разделив переменные

= - К * dτ и проинтегрировав, получим:

К = 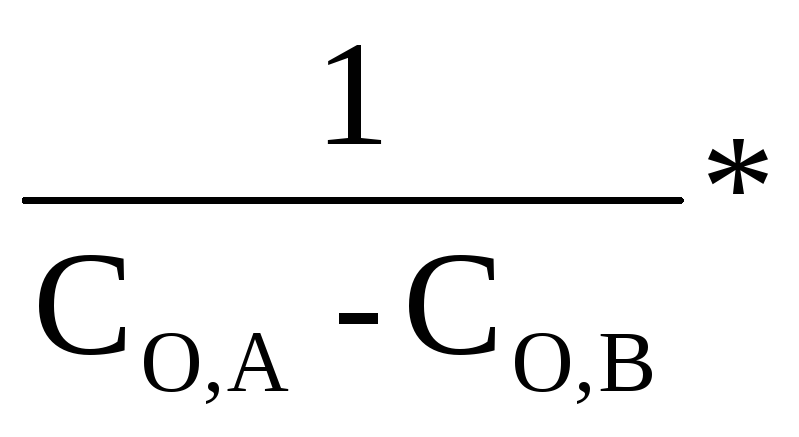ln(2.24)

Кинетические представления о химическом равновесии.

Необратимые и обратимые химические реакции.

Когда при химическом взаимодействии хотя бы одной из исходных веществ расходуется полностью реакцию можно считать протекающей до конца, такую реакцию называют необратимой.

Например, Zn + 4HNO₃ = Zn(NO₃)₂ + 2NO₂ + 2H₂O.

При достаточном количестве азотной кислоты реакция закончится тогда, когда весь Znрасходуется. И если попытаться привести эту реакцию в обратном направлении – пропустить диоксид азота через раствор нитратаZnто, металлическогоZnи азотной кислоты не получится – данная реакция не может протекать в обратном направлении.

Другим примером необратимой реакции может быть разложение бертолетовой соли:

KClO₃ → KCl + 1,5O₂

К необратимым принято относить взаимодействие между веществами, в результате которых образуются осадки, газы или мало диссоциированные соединения.

BaCl₂ + Na₂SO₄ = BaSO₄↓+2NaCl

NaCO₃ + 2HCl = 2NaCl + CO₂↑+ H₂O

Однако каждая из приведенных реакций лишь практически необратима.

В химии растворов электролитов рассматривается возможность процессов.

BaSO₄ → Ba²⁺ + S

CO₂ + H₂O → 2H + C

H₂O → H⁺ + OH^-

Обратимых выделению осадков, газа, образованию мало диссоциированрого соединения. Как показывает опыт, большинство химических реакций протекают одновременно в сторону образования продуктов реакции (вправо, прямая реакция), так и в сторону превращения последних в исходные вещества (влево, обратная реакция). Такие реакции называются химически обратимыми.

Из основного постулата химической кинетики следует, что скорости реакций в любой момент времени, кроме τ = τ_равн, имеют конечную величину. Поэтому с точки зрения термодинамики все они необратимы. Скорость обратимой реакции равна разности между скоростями прямой и обратной реакции в данный момент времени. Если рассмотреть общий случай реакции вида_аА +_вВ_mM +_nN, то скорость прямой реакции определяется уравнением

= -= К₁*(а)

А скорость обратной реакции

== К₂*(в)

Где К₁– константа скорости прямой реакции -

Ка – константа скорости обратной реакции

Если в начальном состоянии системы в ней содержались только вещества А и В, то скорость прямой реакции уменьшается по мере течения ее в соответствии с уменьшением их концентраций. Зависимость этой скорости от времени можно представить кривой I на рисунке (2.3);

Если бы не было обратной реакции, эта кривая достигла бы оси абсцисс при израсходовании одного из исходных веществ. Кривая II, относящаяся к скорости обратной реакции, начинается в начале координат (так как по условию в начальный момент C'_A = C'_В= 0) и повышается по мере течения прямой реакции и вызываемого его увеличения этих концентраций.

Общая скорость реакции в любой данный момент равна разности скоростей прямой и обратной реакции

V = - =*-(2.25)

Очевидно, что при дальнейшем течении реакции указанные две кривые – скоростей прямой и обратной реакции – должны где-то пересечься, т.е. должно быть достигнуто такое состояние, при котором скорости прямой иобратной реакции станут равными между собой. Когда обе скорости сравняются, наступит состояние химического равновесия – концентрации реагирующих веществ становятся вполне определенными и постоянными во времени (при условии, что давление и температура не меняются).

Таким образом, кинетическим условием химического равновесия является равенство скоростей =, а концентрации веществ в равновесной системе называютсяравновесными().

Если скорости равны между собой, следовательно должны быть равны и правые части уравнений (а) и (в).

К₁*= К₂*

Откуда

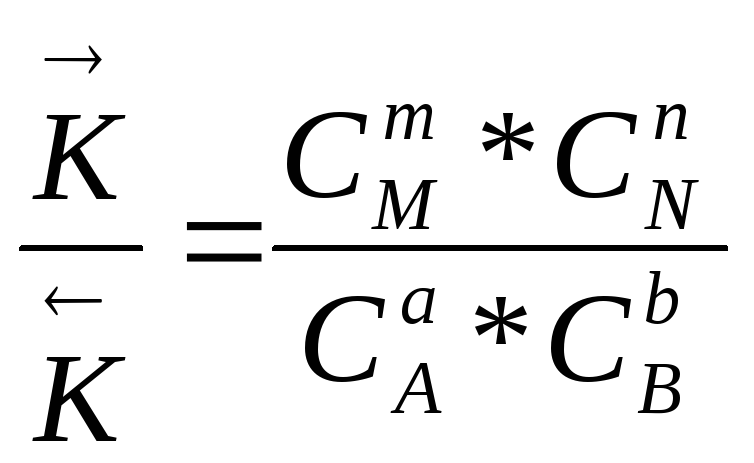
Правая часть равенства представляет собой константу равновесия (Кс) данной реакции

Кс = (2.26)

Следовательно,

Кс = =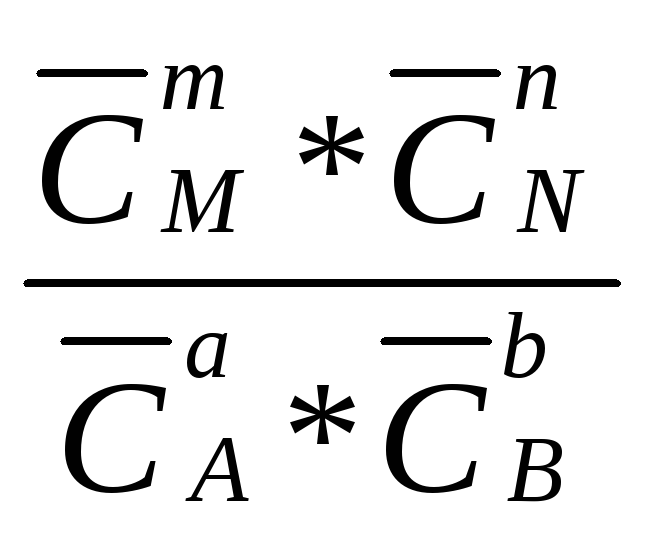(2.27)

Величина, равная отношению произведения равновесных концентраций продуктов реакции к произведению равновесных концентраций исходных веществ в степенях их стехиометрических коэффициентов, называется константой химического равновесия.

Концентрации газообразных веществ в выражении (2.27) могут быть заменены равновесными парциальными давлениями этих веществ.

Кр = =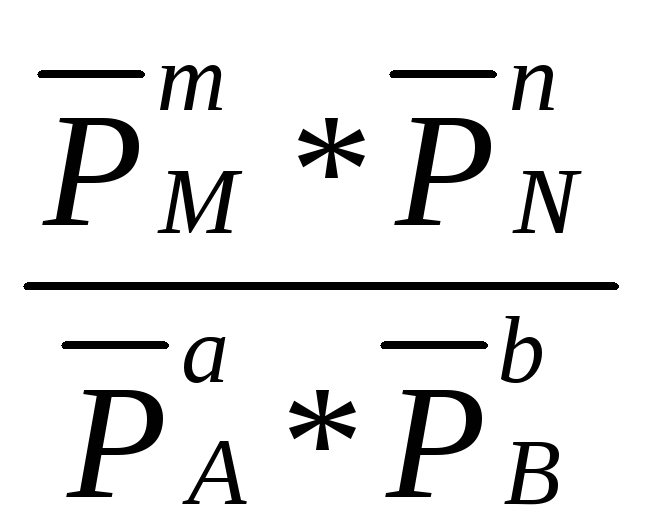(2.28)

(Парциальное давление – давление компонента газовой смеси, которое он имел бы при представлении ему объема занимаемого всей смесью газов).

Если обратимая реакция протекает в гетерогенной системе, в которой наряду с газообразными реагентами участвуют твердые и жидкие вещества (не образующие друг с другом растворов), то при данной температуре парциальные давления реагентов, находящиеся в конденсированном состоянии, постоянны и не зависят от количества реагентов (как и давление постоянного пара какого-либо чистого индивидуального вещества, например воды при данной температуре).

Поэтому эти парциальные давления, независимо от того, малы они или существенны, известны или неизвестны, можно включить в константу равновесия. Следовательно, в подобных случаях в выражении (2.28) следует ввести толь равновесные парциальные давления газообразных веществ.

Так для реакции, FeO_(k) + CO_(г) Fe_(k)+ CO_2(г)

Кр =

Полученные уравнения (2.27) и (2.28) справедливы только для элементарных реакций. В общем случае для сложных превращений, для получения зависимости между величинами Кс, Кр, нужны знания о механизме процессов.

И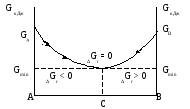так, равенство скоростей (=) является кинетическим условием химического равновесия, но при этом надо помнить, что любая реакция при постоянных температуре и давлении протекает самопроизвольно в направлении убыли энергии Гиббса. Пределом этой убыли является минимальное значение энергии Гиббса. На рисунке 2.4 представлено изменение энергии Гиббса для обратимой реакции (АВ) осуществляемой в закрытой системе в изобарно-изотермических условиях. (Р,Т = const), в зависимости от состава реакционной смеси.

Рис. 2.4 Изменение энергии Гиббса для обратимой реакции (АВ) в зависимости от состава смеси.

Точке А соответствует состав 100 % вещества А, а точке В – 100 % вещества В. Процесс А → В идет самопроизвольно до тех пор, пока величина энергии Гиббса системы уменьшается от G_Aдо G_min , и процесс В → А идет самопроизвольно до тех пор пока G_Вуменьшится до G_min.

Точка С на оси абсцисс отвечающая минимальному значению энергии Гиббса (G_min) определяет равновесный состав смеси при заданных условиях (Р,Т). Состояние равновесия характеризуется равенством_∆G_р,т= 0