
I часть Примеры решения задач
Задача
1. Определить
скорость фотоэлектронов, вырываемых с
поверхности серебра: 1) ультрафиолетовыми
лучами с длиной волны
![]() ;
2)
- лучами с длиной волны
;
2)
- лучами с длиной волны
![]() .
Работа выхода для серебраА
= 4,7 эВ.
.
Работа выхода для серебраА
= 4,7 эВ.
Д ано:Решение
ано:Решение
Уравнение Эйнштейна для фотоэффекта
где
- энергия фотона, падающего на поверхность
металла, А
– работа выхода, Wк
– кинетическая энергия фотоэлектронов.
![]()
![]() ,
(1)
,
(1)
![]()
![]()

![]()
Энергия фотона
![]() (2)
(2)
где
![]() - постоянная Планка,
- постоянная Планка,![]() - скорость света в вакууме,
- длина волны.
- скорость света в вакууме,
- длина волны.
Кинетическая энергия электрона может быть выражена как по классической формуле
![]() (3)
(3)
так и по релятивистской формуле
 ,
(4)
,
(4)
в зависимости от того, какая скорость сообщается фотоэлектрону.
Скорость
фотоэлектрона зависит от энергии фотона,
вызывающего фотоэффект: если энергия
фотона много меньше энергии покоя
электрона
![]() то можно применять формулу (3), если же
энергия фотона сравнима с
то можно применять формулу (3), если же
энергия фотона сравнима с![]() ,
то вычисление необходимо вести по
формуле (4).
,
то вычисление необходимо вести по
формуле (4).
Вычислим энергию покоя электрона:
![]() .
.
Вычислим энергию фотона по формуле (2):
![]()
Энергия фотона много меньше энергии покоя электрона, поэтому
![]() ,
,
откуда
 ,
,
![]()
3.
Вычислим энергию -фотона
![]() Энергия фотона много больше работы
выхода, поэтому можно принять, что
кинетическая энергия электрона равна
энергии фотона. Так как энергия электрона
много больше энергии покоя, то применим
формулу (4):
Энергия фотона много больше работы
выхода, поэтому можно принять, что
кинетическая энергия электрона равна
энергии фотона. Так как энергия электрона
много больше энергии покоя, то применим
формулу (4):
 где
где
![]() .
.
Выполнив преобразования, найдем :
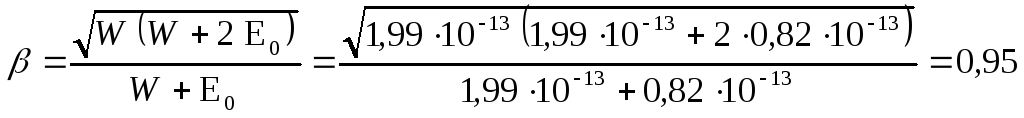 .
.
Откуда
V
=
с
= 0,95 .
3 .
108
= 2,85 .
108
![]() .
.
Ответ:
![]()
Задача
2. Красная
граница фотоэффекта для цезия
![]() .
Определить максимальную скорость
фотоэлектрона при облучении цезия
фиолетовыми лучами с длиной волны
= 4000
.
Определить максимальную скорость
фотоэлектрона при облучении цезия
фиолетовыми лучами с длиной волны
= 4000
![]() .
.
Д ано:Решение
ано:Решение
Уравнение Эйнштейна для фотоэффекта
![]()
![]() .
.
 =
4000
=
4000
![]() = 4.
10-7
м
= 4.
10-7
м
V - ?
Энергия фотона
![]() .
Работа выхода равна энергии фотона с
длиной волны, соответствующей красной
границе фотоэффекта
.
Работа выхода равна энергии фотона с
длиной волны, соответствующей красной
границе фотоэффекта![]() .
Так как энергия фотона видимой части
спектра очень мала по сравнению с
энергией покоя электрона, то кинетическую
энергию электрона выражаем формулой
.
Так как энергия фотона видимой части
спектра очень мала по сравнению с
энергией покоя электрона, то кинетическую
энергию электрона выражаем формулой![]() тогда
получаем
тогда
получаем![]() откуда
откуда

Ответ:
V
= 6,5 .
105
![]() .
.
Задача 3. Источник монохроматического света мощностью Р = 64 Вт испускает ежесекундно 1020 фотонов, вызывающих фотоэффект на пластинке с работой выхода электронов, равной А = 1,6 эВ. До какого потенциала зарядится пластинка при длительном освещении?
Д ано:
Решение
ано:
Решение
Р
Зная
мощность источника и число фотонов
испускаемых ежесекундно найдем энергию
одного фотона
N = 1020 с-1
А = 1,6 эВ = 2,56 . 10-19 Дж
-
? 
![]()
Энергия
фотона
![]() значит
будет наблюдаться фотоэффект, и из
поверхности металла вылетают электроны.
При вылете электронов пластинка
заряжается положительно. Максимальная
кинетическая энергия вырванных электронов
находится из уравнения Эйнштейна для
фотоэффекта
значит
будет наблюдаться фотоэффект, и из
поверхности металла вылетают электроны.
При вылете электронов пластинка
заряжается положительно. Максимальная
кинетическая энергия вырванных электронов
находится из уравнения Эйнштейна для
фотоэффекта
![]() ,
,
откуда
![]() .
.
По мере удаления от пластинки кинетическая энергия электронов убывает, так как они преодолевают электрическое поле, созданное положительно заряженной пластинкой.
При наличии у пластинки определенного потенциала (задерживающего) электрическое поле способно задержать, т.е. возвратить на пластинку вырываемые с ее поверхности электроны. Этот предельный потенциал определяется соотношением
![]()
где е = 1,6 . 10-19 Кл – заряд электрона.
Учитывая уравнение Эйнштейна получим е = Авых, откуда
![]()
Ответ: = 2,4 В.
Задача 4. Вычислить энергию фотона, если в среде с показателем преломления п = 1,33 его длина волны = 5,89 . 107 м.
Д ано:
Решение
ано:
Решение
п
Энергия
фотона вычисляется по формуле
![]() гдеh
= 6,62 .
10-34
Дж·с – постоянная Планка,
- час-
гдеh
= 6,62 .
10-34
Дж·с – постоянная Планка,
- час-
= 5,89 . 107 м
-
? 
тота
света,
![]() - длина волны в вакууме, равная
- длина волны в вакууме, равная![]() ,
где
- длина волны в среде.
,
где
- длина волны в среде.
Тогда
![]()
Ответ: = 2,5 . 10-19 Дж.
Задача
5. В результате
эффекта Комптона фотон при соударении
с электроном был рассеян на угол
![]() Энергия рассеянного фотона
Энергия рассеянного фотона![]() = 0,4 МэВ. Определить энергию фотона
до рассеяния.
= 0,4 МэВ. Определить энергию фотона
до рассеяния.
Д ано:Решение
ано:Решение
Для
определения энергии первичного фотона
воспользуемся формулой Комптона
![]()
![]() где
где![]()
изменение длины волны фотона в результате
изменение длины волны фотона в результате
![]() =
0,4 МэВ
=
0,4 МэВ
-
? 
рассеяния
на свободном электроне,
![]() - масса покоя электрона,
- угол рассеяния фотона.
- масса покоя электрона,
- угол рассеяния фотона.
Тогда
![]() .
.
Откуда

где
![]() - энергия покоя электрона.
- энергия покоя электрона.
Для электрона Е0 = 0,511 МэВ, тогда

Ответ: = 1,85 МэВ.
Задача
6. Фотон с
энергией
= 0,75 МэВ рассеялся на свободном электроне
под углом
= 600.
Принимая, что кинетическая энергия и
импульс электрона до соударения с
фотоном были пренебрежимо малы,
определить: 1) энергию
![]() рассеянного фотона; 2) кинетическую
энергию электрона отдачи.
рассеянного фотона; 2) кинетическую
энергию электрона отдачи.
 Дано:
Решение
Дано:
Решение
Энергию
рассеянного фотона найдем, преобразовав
формулу Комптона
![]() .
.
= 600
![]()
 -
? Wк
- ?
-
? Wк
- ?
Выразив длины волн через энергию фотонов, получим
![]() ,
,
откуда
выразим
![]() :
:


2)
Кинетическая энергия электрона отдачи
по закону сохранения энергии равна
разности между энергией
падающего фотона и энергией
![]() рассеянного фотона:
рассеянного фотона:
![]()
Ответ:
![]()
