Дифракция Фраунгофера на дифракционной решетке

Большое практическое значение имеет дифракция, наблюдаемая при прохождении света через одномерную дифракционную решетку – систему параллельных щелей равной ширины, лежащих в одной плоскости и разделенных равными по ширине непрозрачными промежутками.

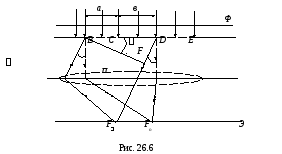
Для наглядности рассмотрим дифракционную решетку, состоящую из двух щелей: BC и DЕ (рис. 26.6). Если ширина каждой щели равна а, а ширина непрозрачных участков между щелями b, то величина d = a + b называется постоянной (периодом) дифракционной решетки. Пусть плоская монохроматическая волна падает нормально к плоскости решетки. Так как щели находятся друг от друга на одинаковых расстояниях, то разности хода лучей, идущих от двух соседних щелей, будут для данного направления  одинаковы в пределах всей дифракционной решетки:

(26.6)

Очевидно, что в тех направлениях, в которых ни одна из щелей не распространяет свет, он не будет распространяться и при двух щелях, т.е. прежние (главные) минимумы интенсивности будут наблюдаться в направлениях, определяемых условием (26.7)

(26.7)

Кроме того, вследствие взаимной интерференции световых лучей, посылаемых двумя щелями, в некоторых направлениях они будут гасить друг друга, т.е. возникнут дополнительные минимумы. Очевидно, что эти дополнительные минимумы будут наблюдаться в тех направлениях, которым соответствуют разность хода лучей ,посылаемых, например, от крайних левых точекB и D обеих щелей. Таким образом, с учетом (26.7) условие дополнительных минимумов:

. (26.8)

Наоборот, действие одной щели будет усиливать действие другой, если

(26.9)

т.е. направлениям (26.9) соответствуют так называемые главные максимумы.

Таким образом, полная дифракционная картина для двух щелей определяется из условий:

- главные минимумы а sin  = , 2 , 3 , . . . ,

- дополнительные минимумы d sin  =

- главные максимумы d sin  = 0, , 2 , 3 , . . . ,

т.е. между двумя главными максимумами располагается один дополнительный минимум.

Аналогично можно показать, что между каждыми двумя главными максимумами при трех щелях располагаются два дополнительных минимума, при четырех щелях – три и т. д.

Если дифракционная решетка состоит из N щелей, то условием главных минимумов является условие (26.7), условием главных максимумов – условие (26.9), а условием дополнительных минимумов:

(26.10)

где может принимать все целочисленные значения, кроме 0,N, 2N, . . . , т.е. кроме тех, при которых условие (26.10) переходит в условие (26.9). Следовательно, в случае N щелей между двумя главными максимумами располагается (N – 1) дополнительных минимумов, разделенных вторичными максимумами, создающими весьма слабый фон.

Примеры решения задач

Задача 1. Интенсивность, создаваемая на экране некоторой монохроматической световой волной, в отсутствие преград равна . Какова будет интенсивностьJ в центре дифракционной картины, если на пути волны поставить преграду с круглым отверстием, открывающим: 1) одну зону Френеля; 2) две зоны Френеля; 3) сто зон Френеля?

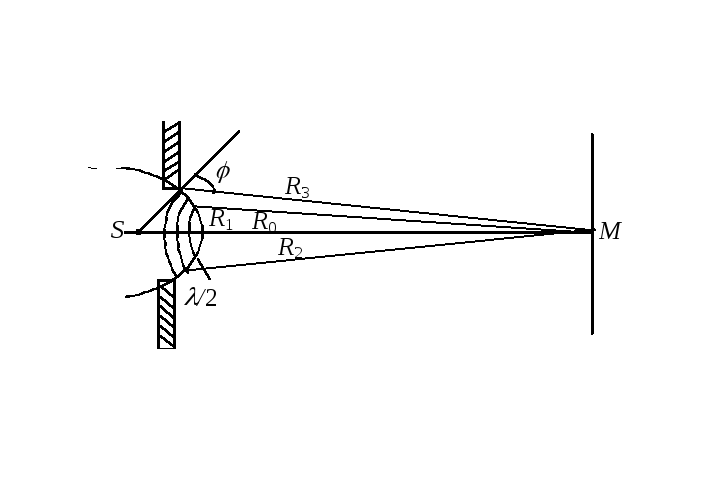
Дано:

J₁ - ? J₂ - ? J₃ - ?

Рис. 26.7