В случае резонанса напряжений
,
поэтому, подставив в эту формулу значения резонансной частоты и амплитуды напряжений на L и С, получим
где
добротность колебательного контура.
Рассмотрим цепь переменного тока, содержащую параллельно включенные конденсатор емкостью С и катушку индуктивностью L (рис. 24.7), R = 0.
Если
приложенное напряжение изменяется по
закону
то согласно формуле
в ветви 1с2
течет ток
амплитуда которого
Начальная фаза этого тока определяется равенством
,
откуда
(24.20)
где т = 1, 2, 3, . . .
Аналогично ток в ветви 1l2
,
амплитуда которого
.
Начальная фаза этого тока
,
откуда
(24.21)
где т = 1, 2, 3, . . .
Из
сравнения выражений (24.20) и (24.21) вытекает,
что разность фаз токов в ветвях 1С2
и 1L2
равна
,
т.е. токи в ветвях противоположны по
фазе. Амплитуда тока в неразветвленной
(внешней) цепи
.
Если
то
и
.
Явление резкого уменьшения амплитуды
силы тока во внешней цепи, питающей
параллельно включенные конденсатор и
катушку индуктивности при приближении
частоты
к резонансной
частоте
называетсярезонансом
токов.
Уравнение плоской волны
,
где - смещение колеблющейся точки; х - расстояние точки от источника волн; V - фазовая скорость распространения волны; - циклическая частота.
Волновое число
,
где
- длина волны,
.
Уравнение волны
.
Связь между разностью фаз и смещением
.
Примеры решения задач
Задача 1. Колебательный контур состоит из конденсатора емкостью 5 мкф и катушки с индуктивностью 0,2 Гн. Омическим сопротивлением цепи пренебрегаем. Максимальное напряжение на обкладках конденсатора 90 В. Записать законы изменения заряда, напряжения и тока со временем. Найти максимальные значения заряда, тока и энергии в колебательном контуре.
Д
ано:Решение
С
В
контуре возникают свободные незатухающие
электромагнитные колебания.
Дифференциальное
уравнение этих колебаний имеет вид
ф
L = 0,2 Гн
В
R
= 0
q(t) ? I ? U ?
Решением этого уравнения является уравнение гармонического колебания
Собственная частота
;
с-1;
Кл.
Уравнение будет иметь вид
Кл.
Зная закон изменения заряда со временем, можно найти любую физическую величину, совершающую колебательное движение.
;
;
В.
Сила тока в контуре
;
А;
А.
Полная энергия электромагнитных колебаний контура складывается из энергии электрического и магнитного полей
Дж.
Максимальную силу тока и полную энергию колебаний можно найти по закону сохранения энергии.
Полная
энергия колебательного контура –
величина постоянная. Когда конденсатор
имеет максимальный заряд
,
напряжение на обкладках конденсатора
,
ток в контуре равен нулю, и полная энергия
равна энергии электрического поля
.
Когда конденсатор разряжен, напряжение на обкладках равно нулю, сила тока достигает максимального значения I0.
Полная
энергия равна энергии магнитного поля
.
Следовательно,
,
откуда находим
;
А.
Полная энергия
Дж.
Ответ:
Кл;
А;
Дж.
Задача
2. Колебательный
контур состоит из конденсатора емкостью
7 мкф,
катушки индуктивностью 0,23 Гн и активным
сопротивлением 40 Ом. Максимальный
заряд на конденсаторе
Кл. Написать закон изменения заряда,
напряжения и силы тока от времени. Найти
период колебаний и логарифмический
декремент затухания.
Д
ано:Решение
В контуре возникают
затухающие колебания.
Закон изменения
заряда со временем
Коэффициент
затухания
.
Гн
Ом
Кл
q(t)
- ?
I(t)
- ?
U(t) - ? T - ? - ?
;
с
.
Период колебаний
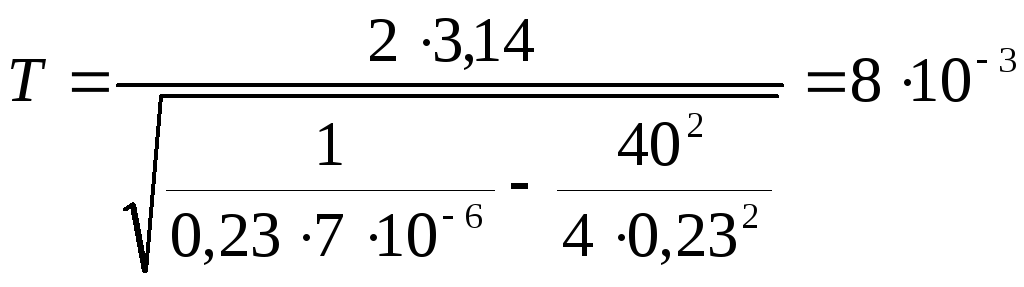с.
откуда
.
Закон изменения заряда со временем
Кл,
тогда
В.
Закон изменения силы тока
;
А.
Логарифмический декремент затухания
.
Ответ:
с;
.
Задача 3. В цепи, состоящей из последовательно соединенных резистора сопротивлением 20 Ом, катушки индуктивностью 1 мГн и конденсатора емкостью 0,1 мкф действует синусоидальная ЭДС, амплитудное значение которой 30 В. Определить частоту ЭДС, при которой в цепи наступит резонанс, и напряжения на всех элементах цепи при резонансе.
Д
ано:Решение
R
Под
действием переменной ЭДС
По закону Ома
в колебательном контуре установятся
вынужденные электромагнитные колебания.
.
L
=
Гн
Ф
В
Амплитуда тока достигает максимального значения (явление резонанса), если емкостное и индуктивное сопротивления равны, т.е.
или
,
откуда
с
;
А.
Напряжение на резисторе
В.
Напряжение на катушке
В.
Напряжение на конденсаторе
В.
будут
во столько раз больше приложенного
напряжения, во сколько раз их сопротивления
больше активного сопротивления.
В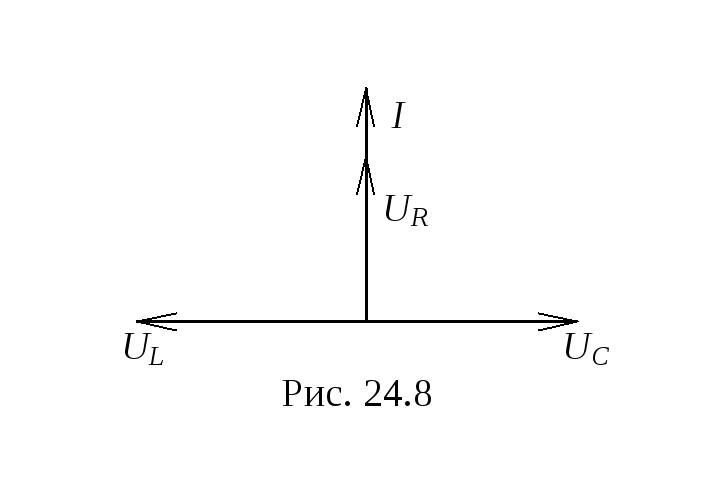
екторная
диаграмма показана на рис. 24.8.
В
за счет обмена энергией между катушкой
и конденсатором,
В идет на покрытие потерь на активном
сопротивлении.
Ответ:
В;
В.
Задача
4. Плоская
продольная упругая волна, распространяющаяся
вдоль оси х,
представлена уравнением
м. Определить частоту колебаний, скорость
распространения волны, длину волны,
амплитуду скорости колебаний каждой
частицы среды.
Д
ано:
Решение
Запишем
уравнение волны в общем виде
и сравним с заданным уравнением
.
Из
сравнения видно, что циклическая частота
,
откуда
;
Гц.
Волновое
число
откуда
.
Из данного уравнения
.
Тогда
м.
Для нахождения скорости колебаний частиц найдем производную по времени от смещения:
;
.
Для нахождения скорости распространения волны используем формулу
,
откуда
;
.
Ответ:
Гц;
;
м;
.
Задача
5. Поперечная
волна распространяется вдоль упругого
шнура со скоростью 15
.
Период колебаний 1,2 с, амплитуда 2 м.
Определить 1) длину волны; 2) Фазу
колебаний, смещение, скорость и ускорение
точки, отстоящей на 45 м от источника, в
момент времениt
= 4 c;
3) Разность фаз двух точек, лежащих на
луче и отстоящих от источника волн на
расстоянии
м
и
м.
Д
ано:Решение
V
1.
Длиной волны называется наименьшее
расстояние между точками волны, колебания
которых отличаются по фазе на 2.
Длина
волны равна расстоянию, которое волна
проходит за один период, поэтому
м.
с
м
м
с
м
м
2. Фазу колебаний, смещение, скорость и ускорение точки можно найти с помощью уравнения волны:
(1)
где
y
- смещение колеблющейся точки; х
- расстояние точки от источника волн;
V-
скорость распространения волн;
- циклическая частота.
Фаза колебаний точки с координатой х в момент времени t равна
так как
то можно записать
;
рад.
Смещение точки определим, подставив в уравнение (1) числовые значения амплитуды и фазы:
м.
Скорость колеблющейся точки
.
Ускорение точки
3. Разность фаз колебаний
.
Ответ:
м;
;
м;
;
;
.
Задача 6. Колебательный контур, состоящий из воздушного конденсатора с двумя пластинами по 100 см2 каждая и катушки индуктивностью 10-6 Гн, резонирует на волну длиной 10 м. Определить расстояние между пластинами конденсатора.
Дано: Решение
Расстояние между
пластинами конденсатора находим из
формулы емкости плоского конденсатора
Гн
м
откуда
.
(1)
Емкость С найдем из формулы Томсона, определяющей период колебаний в контуре:
откуда
.
(2)
Период
колебаний Т
находим из формулы, связывающей длину
волны
и скорость распространения колебаний.
Для электромагнитных колебаний скорость
равна скорости света, тогда
(3)
где
.
Подставив выражение (3) в (2), а затем в (1), получим
и
м.
Ответ:
м.