Решение

При построении графика нужно учесть: 1) газ сжимается, т. е. V₂ < V₁ 1 - 2 - адиабата; 2) в процессе охлаждения V₂ = V₃ = const, следовательно, процесс изохорный, давление р уменьшается; 3) так как по условию Т₃ = Т₁, то через точки 1 и 3 можно провести изотерму. При решении используем уравнение изотермы рV = const, или V₁ = V₂ (V₂ = V₃, так как процесс 2 - 3 изохорный).

Тогда

м³.

Давление найдем из уравнения адиабаты:

.

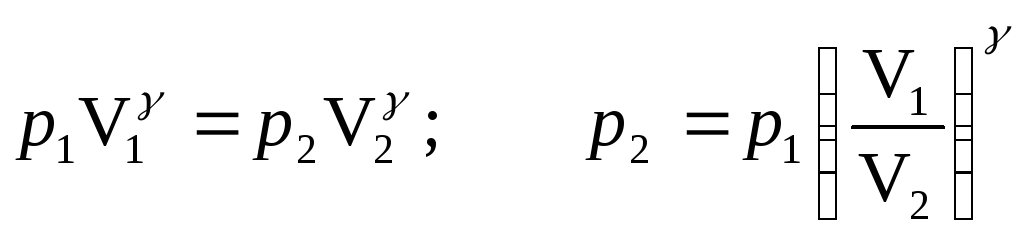Показатель адиабаты , так какi = 5 (газ двухатомный).

Па.

Ответ: V₂ = 0,25 ^. 10^–3 м³; Р₂ = 1,32 ^. 10⁵ Па.

Задача 4. В сосуде под поршнем находится гремучий газ, занимающий объем 10^–4 м³ при нормальных условиях. При быстром сжатии газ воспламеняется. Найти температуру воспламенения гремучего газа, если работа сжатия равна 47,3 Дж.

Дано:Решение

V

Гремучий газ представляет собой смесь двухатомных газов – кислорода и водорода, число степеней свободы i = 5.

Процесс сжатия проходит быстро, теплообмен с окружающей средой не успевает произойти, следовательно, Q = 0, т. е. процесс можно считать адиабатическим.

= 10^–4 м³

= 10⁵ Па

Т₁ = 273 К

А = 47,3 Дж

Т₂ - ?

Применив первое начало термодинамики к адиабатическому процессу, получим

Q = 0; U =  A.

Сжатие совершают внешние силы, работа внешних сил считается отрицательной; внутренняя энергия газа возрастает за счет совершенной внешними силами работы. Температура газа повышается

,

где Т = Т₂ – Т₁.

Тогда работа

Согласно уравнению Менделеева – Клапейрона,

откуда

Тогда

К.

Ответ: Т₂ = 775 К.

Задача 5. Автомобильная шина была накачана до давления = 2,2 атм при температуреt₁ = 15 ⁰С; во время движения она нагрелась до t₂ = 55 ⁰С и лопнула. На сколько градусов охладился вышедший из шины воздух (процесс считать адиабатическим).

Дано:Решение

По условию задачи в шине протекают два процесса: 1) изохорное нагревание (V = const), 2) адиабатное расширение (Q = 0).

1. для изохорного процесса:

,

= 2,2 атм

t₁ = 15 ⁰С; Т₁ = 288 К

t₂ = 55 ⁰С; Т₂ = 328 К

= 1 атм

Т₂ - ?

. (1)

2) для адиабатического процесса

;

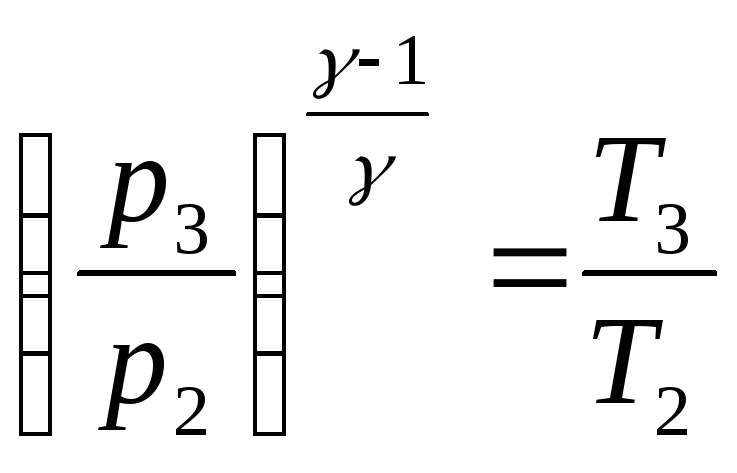. (2)

Из уравнения (1)

 = 1,4; Т₃ – температура после адиабатического расширения.

Вычислим

;

Т₃ = 0,76 ^. Т₂ = 250 К;

Т₂ = Т₃ – Т₂ = (250 – 328) К = – 78 К.

Ответ: воздух охладился на 78 К.

Задача 6. Чему равна теплоемкость идеального газа в изотермическом и в адиабатическом процессе.

Решение

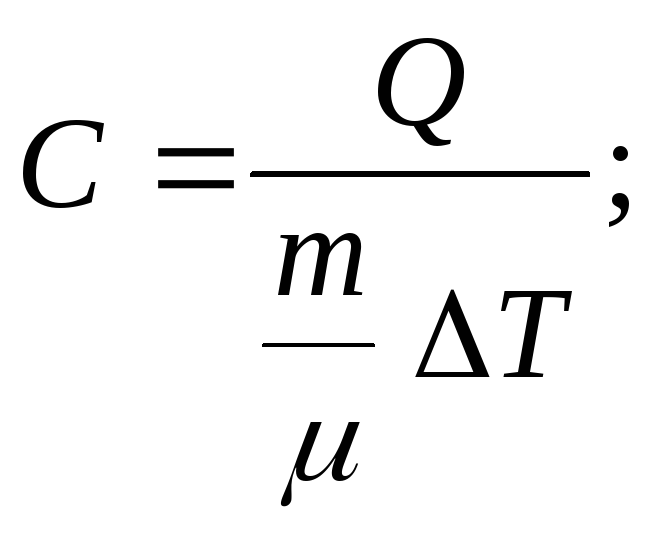
Дано:

а) T = const

б) Q = 0

С₁ - ? С₂ - ?

а) Т = 0; С₁  .

б) Q = 0; С_2­ = 0.

Ответ: С₁  ; С_2­ = 0.

Задача 7^*. На рис.21.5 показан обратимый переход идеального двухатомного газа из состояния 1 в состояние 2. Процесс состоит из изотермического участка 1 - 3 и адиабатического участка 3 - 2. В начальном состоянии V₁ = 10^–3 м³, = 3^. 10⁵ Па в конечном состоянии V₂ = 2 ^. 10^–3 м³, = 1,33^. 10⁵ Па. Вычислить работу, совершенную газом в процессе перехода 1 - 3 - 2.

Дано:

V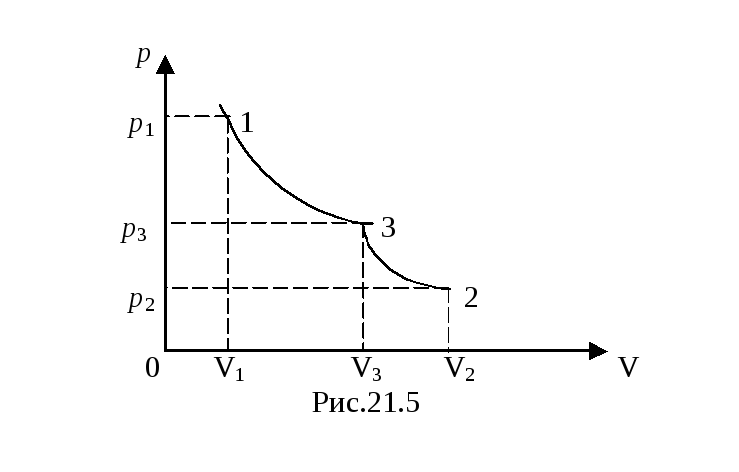₁ = 10^–3 м³

V₂ = 2 ^. 10^–3 м³

= 3 ^. 10⁵ Па

= 1,33 ^. 10⁵ Па

А_1-2 – ?