I часть Примеры решения задач

Задача 1. 10 г кислорода находятся под давлением 3 ^. 10⁵ Па при температуре 10⁰С. После нагревания при постоянном давлении газ занял объем 10 л. Найти: 1) количество тепла, полученное газом; 2) изменение внутренней энергии газа; 3) совершенную газом работу.

Решение

1. р = const; процесс изобарный.

2. Q = U + A, где Q – количество тепла, сообщенное газу; U – изменение внутренней энергии газа; А – совершенная газом работа.

3. а) Элементарная работа

Дано:

т = 10 г = 10 ^–2 кг

 = 32 ^. 10^-3

р = 3 ^. 10⁵ Па = const

t = 10⁰ С; Т = 283 К

V₂ = 10 л = 10^-2 м³

А - ? U - ? Q - ?

где р – давление газа; dV – бесконечно малое изменение его объема. Из условия задачи видно, что dV > 0, т.е. газ расширяется, тогда работа А > 0, т.е. работа совершается газом против внешних сил. Полная работа расширения

.

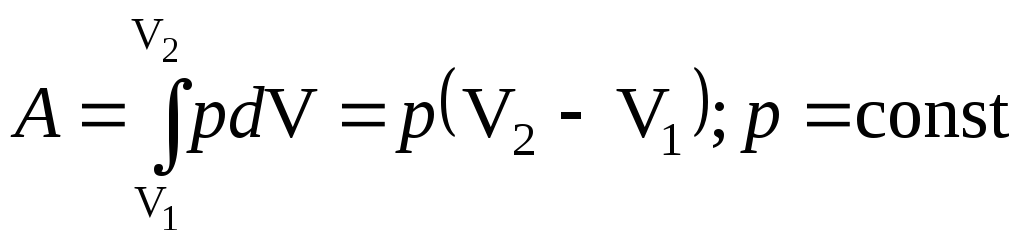б) Изменение внутренней энергии равно

где Т – изменение температуры; i – число степеней свободы молекулы кислорода (i = 5, так как кислород – двухатомный газ).

в) Количество теплоты, полученное газом при нагревании, может быть найдено как сумма А и U, или с помощью молярной теплоемкости С_р:

4. Решим задачу численно, сделав некоторые преобразования формул и вычислив недостающие параметры газа.

1) (1)

Используем два уравнения Менделеева - Клапейрона для состояния 1 и 2:

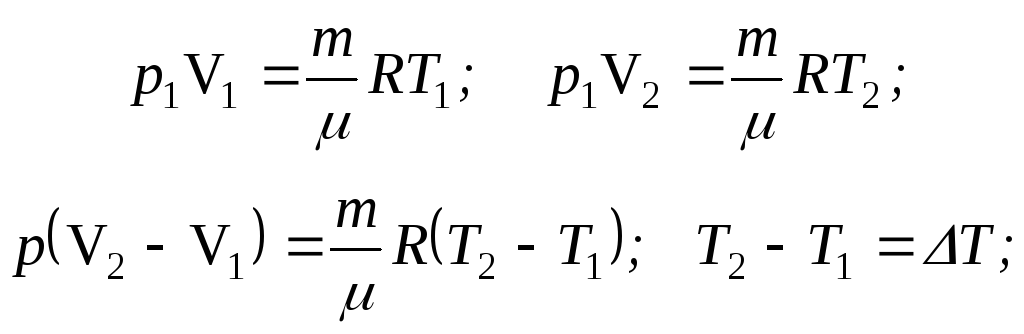
(1')

(справедливо только для изобарного процесса)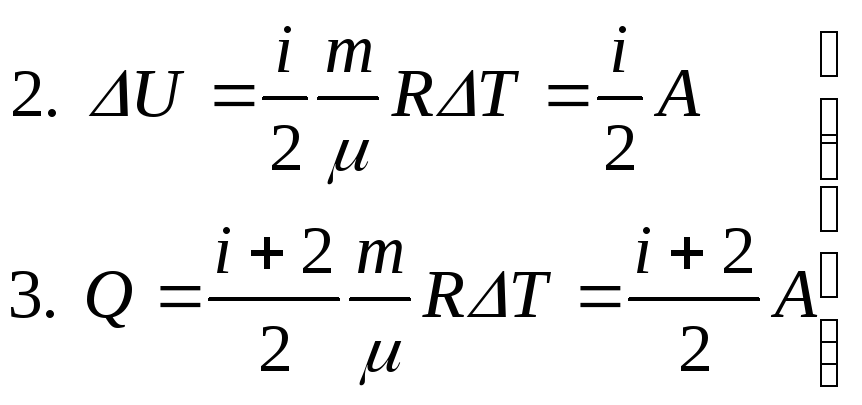

Найдем Т: Т = Т₂ – Т₁; - из уравнения Менделеева - Клапейрона для второго состояния.

Т = Т₂ – Т₁ =

Тогда работа

Дж.

Изменение внутренней энергии

Дж.

Количество теплоты

Дж.

Можно определить работу по формуле (1); для этого нужно найти объем газа V₁ из уравнения состояния:

.

Ответ: А = 2265 Дж; U = 5660 Дж; Q = 7920 Дж.

Задача 2. В закрытом сосуде объемом V = 10 л находится воздух при давлении 10⁵ Па. Какое количество теплоты нужно сообщить газу, чтобы повысить его давление в 5 раз?

Дано:Решение

V = 10 ^–2 м³ 1) Из условия задачи следует, что процесс изохорный,

р₁ = 10 ⁵ Па так как сосуд закрытый. Следовательно, V = const.

р₂ = 5р₁ 2) Q = U + A – первое начало термодинамики.

i = 5 3) Применим I начало к изохорному процессу:

Q - ? а) следовательноА = 0;

б) ;

в) .

4. Вычислим разность температур, пользуясь уравнениями состояния для 1 и 2 состояний:

.

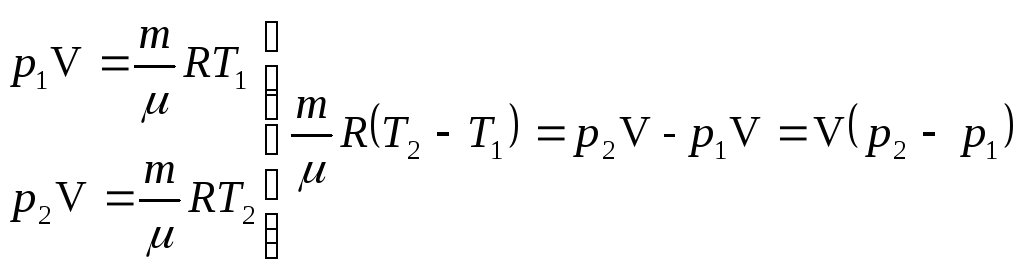Тогда

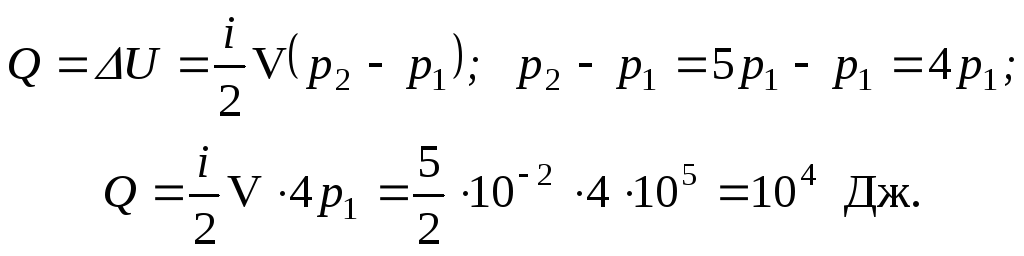
Ответ: Q = 10⁴ Дж.

Задача 3. Некоторая масса азота при давлении р₁ = 1 атм имела объем V₁ = 5 л, а при давлении р₂ = 3 атм – объем V₂ = 2 л. Переход от первого состояния ко второму сделан в два этапа – сначала по изохоре, затем по изобаре. Определить изменение внутренней энергии, количество теплоты и произведенную работу.

Дано:Решение

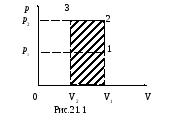= 28 ^. 10^-3

i = 5

p₁ = 1 атм = 10⁵ Па

р₂ = 3 атм = 3 ^. 10⁵ Па

V₁ = 5 л = 5 ^. 10^-3 м³

V₂ = 2 л = 2 ^. 10^-3 м³

U - ? A - ? Q - ?

1) V = const – I процесс; р = сonst – II процесс.

I процесс – изохорное нагревание; II процесс – изобарное сжатие.

2) Первое начало термодинамики

3) а) ;

Работа в изобарном сжатии на участке 2-3 отрицательна, так как объем газа уменьшается, газ сжимается под действием внешних сил:

.

б)

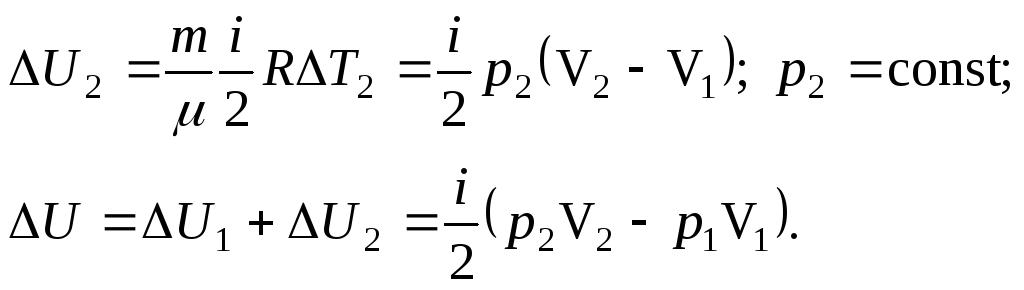
Изменение внутренней энергии зависит только от начального и конечного состояния системы и не зависит от пути перехода.

в) Q = U + A.

Вычисления:

– работу совершают внешние силы.

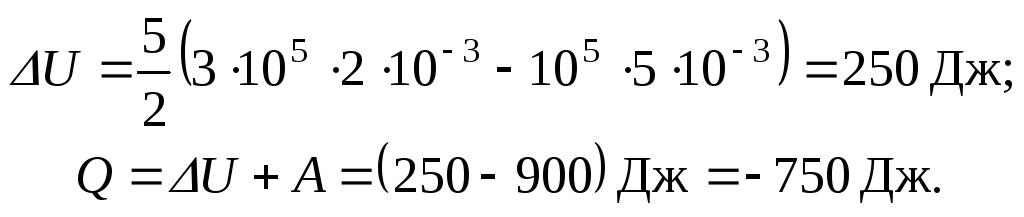
Работа совершается над газом, тепло отводится от газа, газ нагревается (U > 0).

Ответ: А = -900 Дж; U = 250 Дж; Q = -750 Дж.

Задача 4. Один моль воздуха при давлении р₁ = 10⁶ Па и температуре Т₁ = 390 К изохорически изменяет давление так, что его внутренняя энергия изменяется на U = - 71,7 Дж, а затем изобарически расширяется и совершает работу А = 745 Дж. Определить параметры воздуха, если удельная теплоемкость  = 28 ^. 10^-3 .

Дано: Решение

моль I. В задаче рассматриваются два процесса:

 = 28 ^. 10^-3 1) V = const и 2) р = const.

Т₁ = 390 К II. Рассмотрим I процесс (изохорный) (рис. 21.2):

р

р

р₁ 1 Т₁

р₂ 2 Т₂ 3

Т₃

0

V₁ V₂ V

Рис.21.2

₁ = 10⁶ Па

U = -71,7 Дж

А = 745 Дж

Т₂ - ? Т₃ - ?

а) .

б) Q₁= U₁ – первое начало в изохорном процессе.

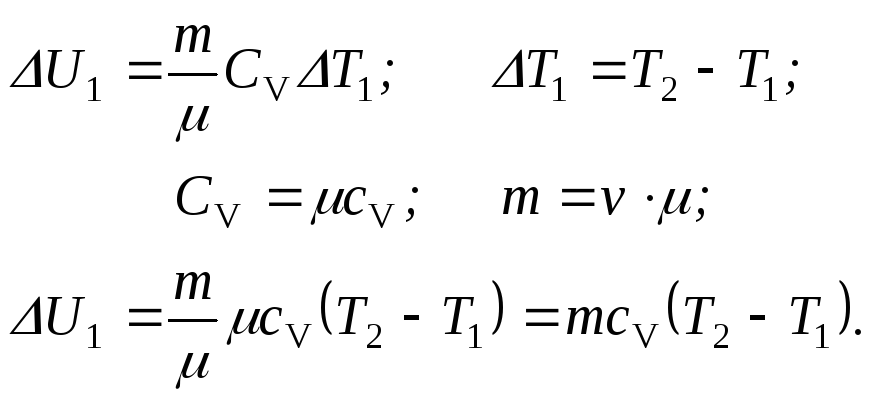
Тогда

III. Второй процесс – изобарное расширение:

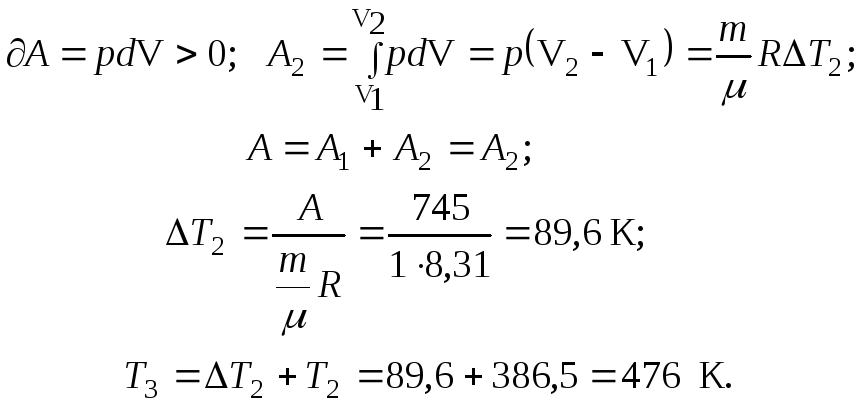
Из уравнения состояния идеального газа и законов Гей-Люссака и Шарля можно получить остальные параметры:

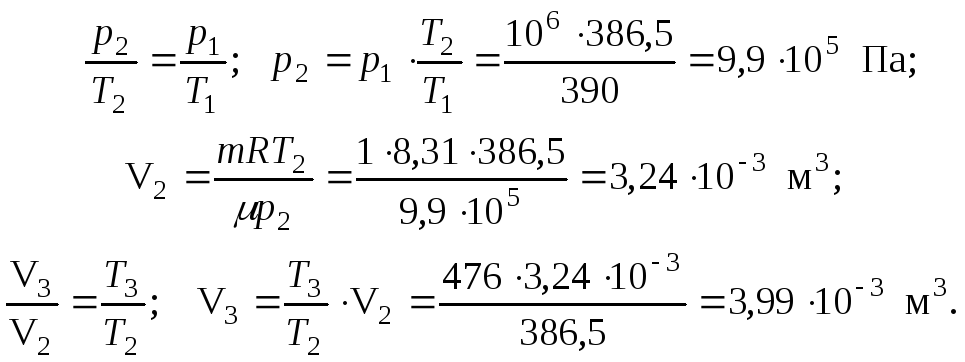
Ответ: р₂ = 9,9 ^. 10⁵ Па; Т₂ = 386,5 К; V₂ = 3,24 ^. 10^-3 м³; р₃ = р₂; Т₃ = 476 К; V₃ = 3,99 ^. 10^-3 м³.

Задача 5. 10,5 г азота изотермически расширяются при температуре –23 ⁰С от р₁ = 2,5 атм до р₂ = 1 атм. Найти работу, совершенную при расширении, изменение внутренней энергии и количество тепла, переданное газу.

Дано:Решение

т

По условию задачи T = const, процесс изотермический

Q = U + A.

a) A = pdV; dV > 0; A > 0;

б) ;

в) Q = A все переданное газу тепло идет на работу газа против внешних сил.

= 10,5 г = 10,5 ^. 10^-3 кг

 = 28 ^. 10^-3

t₁ = -23⁰ C; T₁ = 250 К

р₁ = 2,5 атм = 2,5 ^. 10⁵ Па

р₂ = 1 атм = 1 ^. 10⁵ Па

А - ? U - ? Q - ?

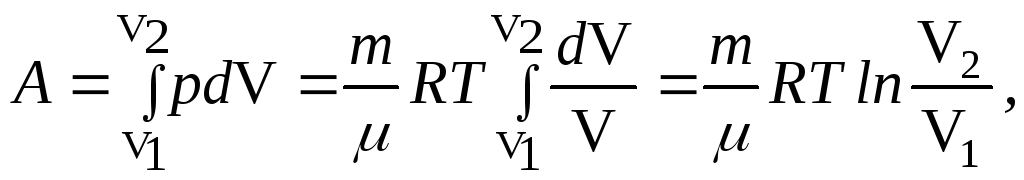
так как процесс изотермический, то т.е.

Ответ: А = 713,8 Дж.

Задача 6. 7 г углекислого газа СО₂ было нагрето на Т = 10 К в условиях свободного расширения. Найти работу расширения газа и изменение его внутренней энергии.

Дано:Решение

i

1) Свободное расширение газа означает, что его давление не изменяется, т.е. p = const, процесс изобарный.

2) Q = U + A;

a);

= 6

m = 7 ^. 10^-3 кг

 = 44 ^. 10^-3

Т = 10 К

А - ? U - ?

;

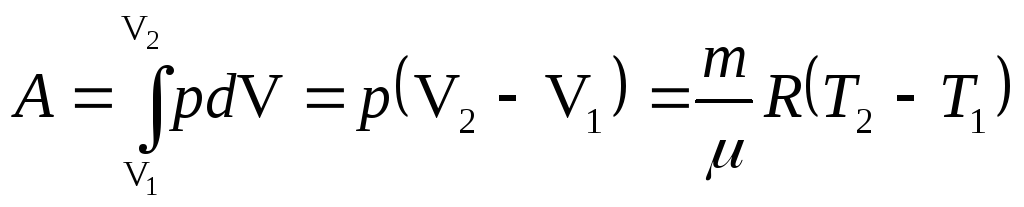T₂ – T₁ = T;

б) .

Вычисления:

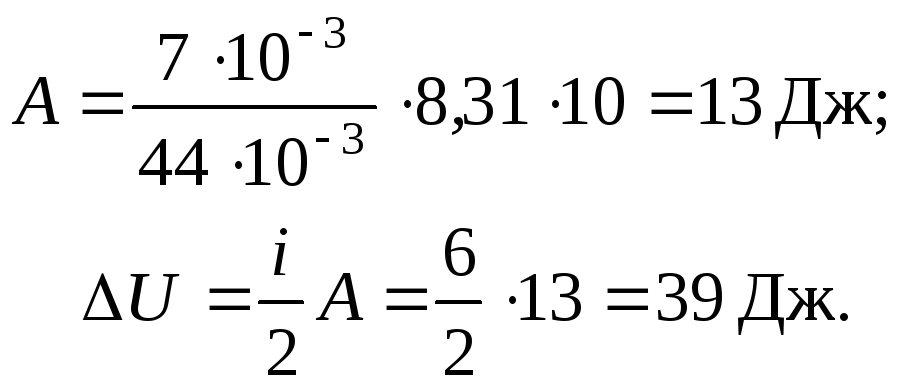
Ответ: А = 13 Дж; U = 39 Дж.