Решение типовых примеров по Заданию 10
10.1. Вычислить определенный интеграл по формуле Ньютона-Лейбница, а затем по формуле Симпсона, разбив отрезок интегрирования на 10 равных частей.
Вычисления производить с точностью до четвертого знака. Определить абсолютную и относительную ошибки вычислений.
.
Решение. Вычислим интеграл по формуле Ньютона-Лейбница.
.
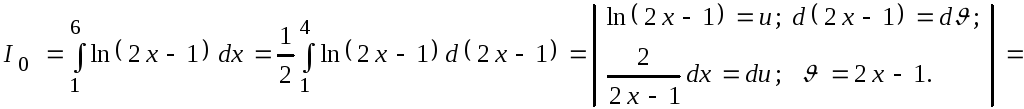
Вычислим определенный интеграл по формуле Симпсона.
;
;
;
;
;
;
;
.
;
.
;
По формуле Симпсона
.
.
В нашем случае
.
.
Абсолютная погрешность вычислений
.
Относительная погрешность
.
10.2. Вычислить определенный интеграл по формуле Ньютона-Лейбница, а затем по формуле трапеций, разбив отрезок интегрирования на 8 равных частей.
Вычисления производить с точностью до четвертого знака. Определить абсолютную и относительную ошибки вычислений.
.
Решение. Вычислим интеграл по формуле Ньютона-Лейбница.
.
Вычислим интеграл по формуле трапеций.
Разобьем отрезок интегрирования на 8 частей и составим таблицу значений подынтегральной функции
,
;
,
;
,
;
,
;
,
;
,
;
,
;
,
.
,
;
По формуле трапеций 
.
В нашем случае
.
.
Абсолютная погрешность вычислений
.
Относительная погрешность
.
Задания расчетно-графической работы Задание 1
Найти неопределенные интегралы
методом непосредственного интегрирования:
сведением интеграла к табличному;
,
пользуясь инвариантностью формулы
интегрирования (подведением функции
под знак дифференциала).
Результаты
проверить путем нахождения произ-водной
от полученной функции.
1.1.
;
;
;
; 
;
.
1.2.
;
;
;
; 
;
.
1.3.
;
;
;
; 
;
.
1.4.
;
;
;
; 
; 
.
1.5.
;
;
; 
;
.
1.6.
;
;
;
;
;
.
1.7.
;
;
;
;
;
.
1.8.
;
;
;
;
;
.
1.9.
;
;
;
;
;
.
1.10.
;
;
;
;
;
.
1.11.
;
;
;
;
;
.
1.12.
;
;
;
;
;
.
1.13.
;
;
;
;
;
.
1.14.
;
;
;
;
; 
.
1.15.
;
;
;
;
;
.
1.16.
;
;
;
; 
;
.
1.17.
;
;
;
; 
;
.
1.18.
;
;
;
; 
;
.
1.19.
;
;
;
; 
;
.
1.20.
;
;
;
; 
;
.
1.21.
;
;
;
; 
;
.
1.22.
;
;
;
; 
;
.
1.23.
;
;
;
; 
;
.
1.24.
;
;
;
; 
;
.
1.25.
;
;
;
; 
;
.
1.26.
;
;
;
; 
;
.
1.27.
;
;
;
; 
;
.
1.28.
;
;
;
; 
;
.
1.29.
;
;
;
; 
;
.
1.30.
;
;
;
; 
;
.
Задание 2
Найти неопределенные интегралы методом замены переменной
2.1.
.
2.2.
.
2.3.
.
2.4.
.
2.5.
. 2.6.
.
2.7.
. 2.8.
. 2.9.
.
2.10.
. 2.11.
. 2.12.
.
2.13.
. 2.14.
. 2.15.
.
2.16.
. 2.17.
. 2.18.
.
2.19.
. 2.20.
. 2.21.
.
2.22.
. 2.23.
. 2.24.
.
2.25.
2.26.
.
2.27.
.
2.28.
. 2.29.
.
2.30.
.
Задание 3
Найти неопределенные интегралы, используя метод интегрирования по частям
3.1. а)
;б)
.
3.2. а)
;б)
.
3.3. а)
;б)
.
3.4. а)
;б)
.
3.5. а)
;б)
.
3.6. а)
;б)
.
3.7. а)
;б)
.
3.8. а)
;б)
.
3.9. а)
;б)
.
3.10. а)
;б)
.
3.11. а)
;б)
.
3.12. а)
;б)
.
3.13. а)
;б)
.
3.14. а)
;б)
.
3.15. а)
;б)
.
3.16. а)
;б)
.
3.17. а)
;б)
.
3.18. а)
;б)
.
3.19. а)
;б)
.
3.20. а)
;б)
.
3.21. а)
;б)
.
3.22. а)
;б)
.
3.23. а)
;б)
.
3.24. а)
;б)
.
3.25. а)
;б)
.
3.26. а)
;б)
.
3.27. а)
;б)
.
3.28. а)
;б)
.
3.29. а)
;б)
.
3.30. а)
;б)
.
Задание 4
Найти неопределенные интегралы
от рациональных функций:
используя выделение полного квадрата;
пользуясь разложением рациональных
дробей на простейшие.
4.1. а)
;б)
.
4.2. а)
;б)
.
4.3. а)
;б)
.
4.4. а)
;б)
.
4.5. а)
;б)
.
4.6. а)
;б)
.
4.7. а)
;б)
.
4.8. а)
;б)
.
4.9. а)
;б)
.
4.10. а)
;б)
.
4.11. а)
;б)
.
4.12. а)
;б)
.
4.13. а)
;б)
.
4.14. а)
;б)
.
4.15. а)
;б)
.
4.16. а)
;б)
.
4.17. а)
;б)
.
4.18. а)
;б)
.
4.19. а)
;б)
.
4.20. а)
;б)
.
4.21. а)
;б)
.
4.22. а)
;б)
.
4.23. а)
;б)
.
4.24. а)
;б)
.
4.25. а)
;б)
.
4.26. а)
;б)
.
4.27. а)
;б)
.
4.28. а)
;б)
.
4.29. а)
;б)
.
4.30. а)
;б)
.