Решение типовых примеров по Заданию 7

7.1. Вычислить площадь фигуры, ограниченной графиками функций ;;;. Построить графики.

Решение. Построим графики заданных функций (рис. 2.6).

Переменнаяизменяется

от до, а функцияот

до .

Согласно формулы (2.4)

искомая площадь фигуры равна

Рис. 2.6

(кв. ед.).

7.2. Вычислить площадь фигуры, ограниченной графиками функций ;. Построить графики.

Решение.Построим графики заданных функций (рис. 2.7).

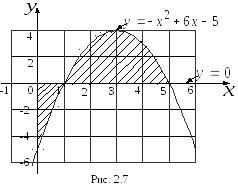
Согласно формулы (2.5) искомая площадь фигуры равна

(кв. ед.).

7.3. Найти площадь фигуры, ограниченной графиками функций и.

Решение. Найдем точки пересечения кривых, решая совместно систему уравнений

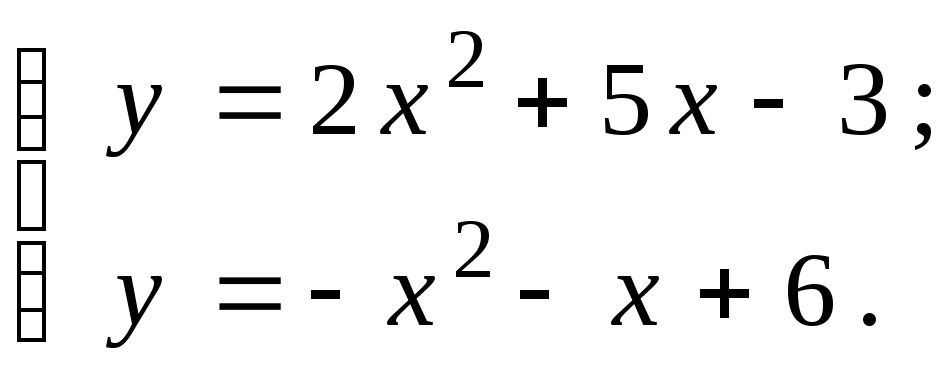
Построим графики.

Рис. 2.8

Переменная изменяется отдо, а функцияотдо.

Искомая площадь

(кв. ед.).

2.4.2. Вычисление длины дуги

. Если плоская кривая задана в прямоугольной декартовой системе координат уравнением (или, то дифференциал длины дуги определяется по формуле

.

Интегрируя дифференциал дуги в заданных пределах, находим длину дуги

, (2.8)

где .

. Если плоская кривая задана в полярной системе координат уравнением , то дифференциал длины дуги равен

,

а длина дуги определяется по формуле

. (2.9)

где .

Решение типовых примеров по Заданию 8

8.1. Найти площадь фигуры, ограниченной кривыми, заданными в полярных координатах ;,.

Решение. Площадь криволинейного сектора, ограниченного кривой, заданной в полярных координатах уравнением , и двумя полярными радиусами, составляющими с полярной осью углыивычисляется по формуле (2.7)

(кв. ед).

8.2. Найти длину дуги параболы от точкидо точки.

Решение. Поскольку ,а , то по формуле (2.8) получим

(ед. длины).

При вычислении интеграла воспользовались формулой 24 таблицы основных интегралов.

8.3. Найти длину дуги кривой ;.

Решение. Длина дуги кривой, заданной в полярных координатах, вычисляется по формуле (2.9).

В нашем случае .

(ед. длины).

2.4.3. Вычисление объемов тел вращения

Если тело образовано вращением вокруг оси кривой, то объем тела вращения вычисляется по формуле

, (2.10)

Если кривая ,вращается вокруг оси, объем тела вращения в этом случае равен

, (2.11)

Решение типовых примеров по Заданию 9

9.1. Найти объем тела, образованного вращением вокруг оси фигуры, расположенной в первом квадранте и ограниченной параболой, прямойи осью. Сделать чертеж.

Решение. Найдем абсциссу точки пересечения параболы и прямой в первом октанте. Для этого решим уравнение или. Решая его, получаем,.Первому квадранту соответствует корень .

Найдем теперь абсциссу точки пересечения прямой с осью Ох, решив уравнение , откуда.Сделаем чертеж (рис. 2.9).

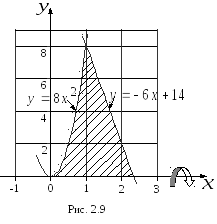
Таким образом, тело вращения ограничено при поверхностью, образованной вращением параболывокруг оси, а привращением прямой.

Объем тела вращения вычислим по формуле (2.10):

.

Для вычисления второго интеграла используем подстановку .

(куб.ед).