1.3.6. Интегрирование тригонометрических функций

. Интегралы вида. Выделим здесь три случая, имеющие особенно важное значение.

1. Если оба показателя степени ичетные положительные числа, то следует преобразовывать подынтегральную функцию с помощью формул

, ,.

2. Интеграл от нечетной степени или(или ии) можно найти путем отделения от нее одного множителя и применения подстановки:

еслинечетное положительное число;

еслинечетное положительное число.

3. Если , то есть четное отрицательное число, тоцелесообразно использовать подстановку , откуда;,.

. Интегралы вида, гдерациональная функция. Приводятся к интегралам от рациональных функций с помощью так называемойуниверсальной тригонометрической подстановки .В результате этой подстановки имеем:

; ;

; .

Примечание: Универсальная подстановка во многих случаях приводит к сложным вычислениям, так как при ее применении ивыражаются черезв виде рациональных дробей, содержащих.

В некоторых случаях нахождение интегралов вида может быть упрощено.

1. Если нечетная функция относительно, т.е. если, то интеграл рационализируется подстановкой.

2. Если нечетная функция относительно, т.е. если, то интеграл рационализируется подстановкой.

3. Если четная функция относительно, ит.е. если, то к цели приводит подстановка.

Интегралы вида ,, гдецелое положительное число. При нахождении таких интегралов применяется формула(или), с помощью которой последовательно понижается степень тангенса или котангенса.

Интегралы вида ,,приводятся к табличным путем разложения подынтег-ральных функций на слагаемые по формулам:

,

,

.

Решение типовых примеров по Заданию 5

а) 5.1. .

Решение. Имеем интеграл вида . Наименьший общий знаменатель дробейиравен 6, поэтому, делаем подстановку:. Тогда

.

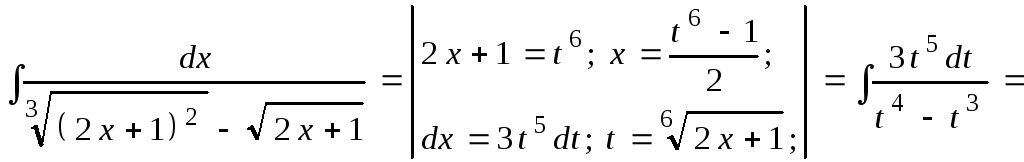
б) 5.2. .

Решение. Это интеграл вида Здесь,четные положительные. Применим формулу понижения степени и преобразования произведения:

.

5.3. .

Решение. Интеграл вида нечетное. Отделим от нечетной степени один множитель первой степени, внесем его под знак дифференциала и сделаем подстановку.

.

2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ

2.1. Формула Ньютона-Лейбница.

Если есть первообразная от непрерывной функции, то справедлива формула

. (2.1)

По формуле Ньютона-Лейбница сначала находят первообразную, а затем находят разность первообразных, соответственно при верхнем и нижнем значении предела.

2.2. Замена переменной в определенном интеграле

Пусть дан интеграл где функциянепрерывна на отрезке. Введем новую переменнуюпо формуле.

Если ,; функцияи ее производнаянепрерывны на отрезкеиопределена и непрерывна на отрезке, то

. (2.2)

2.3. Интегрирование по частям

Если функции иимеют непрерывные производные на отрезке, то справедлива формула

. (2.3)

Решение типовых примеров по Заданию 6

6.1. .

Решение.

.

2.4. Приложения определенного интеграла

2.4.1. Вычисление площади плоской фигуры

. Если непрерывная кривая задана уравнением ,, то площадь криволинейной трапеции, прилежащей к оси(рис. 2.1) вычисляется по формуле

. (2.4)

Если фигура расположена по разные стороны оси (рис. 2.2), то площадьследует вычислять по формуле

. (2.5)

. Если фигура ограничена двумя непрерывными кривыми и, прилегающими к оси(рис. 2.3, 2.4), то ее площадь равна разности площадей соответствующих криволинейных трапеций и определяется по формуле

. (2.6)

. Площадь плоской фигуры

в полярной системе координат

может быть составлена из площадей

криволинейных секторов (рис. 2.5)

и вычисляется по формуле

. (2.7)