Решение типовых примеров по Заданию 3

3.1. .

Решение. Это интеграл типа В этом случае. Поэтому

.

3.2. .

Решение. Это интеграл типа В этом случае.

.

1.3.4. Интегрирование рациональных функций

Приведем несколько рекомендаций.

. При вычислении интегралов, содержащих квадратный трехчлен вида

выделяют полный квадрат из квадратного трехчлена в знаменателе, после этого применяют формулы табличных интегралов 2, 18, 19.

. Интегрирование рациональных дробей с помощью разложения на простейшие дроби.

Перед интегрированием рациональной дроби надо сделать следующие алгебраические преобразования и вычисления:

1. Если дана неправильная рациональная дробь, то выделить из нее целую часть (как было указано выше), то есть представить в виде

.

2. Разложить знаменатель на простые множители.

При этом могут встретиться следующие случаи:

а) корни знаменателя действительны и различны;

б) корни знаменателя действительные и некоторые из них кратные;

в) среди корней знаменателя есть комплексные;

г) среди корней знаменателя есть комплексные кратные.

В общем виде разложение имеет вид

,

где , то есть трехчленимеет комплексные сопряженные корни.

3. Правильную рациональную дробь разложить на простейшие дроби:

.

Для каждого множителя в разложении знаменателя выписывается столько простых дробей, какова его кратность. Знаменателями простых дробей являются целые числа степени каждого множителя, начиная с первого и кончая той степенью, которую множитель имеет в разложении.

4. Вычислить неопределенные коэффициенты ,, . . . ,, . . . ,

,,,. . . ,,. . .

Решение типовых примеров по Заданию 4

4.1. .

Решение.Это интеграл вила. Выделим в знаменателе полный квадрат и сделаем замену переменной.

.

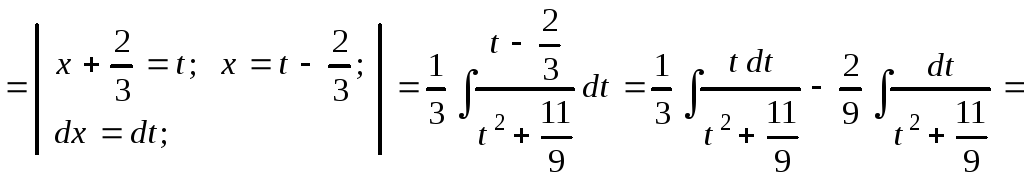
4.2. .

Решение. Это случай. Знаменатель имеет только действительные различные корни.

Так как каждый из двучленов входит в знаменатель в первой степени, то данная правильная дробь может быть представлена в виде суммы следующих простейших дробей:

.

Приводя к общему знаменателю правую часть равенства, и приравнивая числители полученных дробей, имеем

.

Следовательно,

.

Раскроем скобки и сгруппируем члены с одинаковыми степенями:

.

Сравнивая коэффициенты при одинаковых степенях , получим систему уравнений

из которой находим ,,.

Итак, разложение рациональной дроби на простейшие имеет вид

.

Таким образом,

.

1.3.5. Интегрирование простейших иррациональных функций

Интегралы от иррациональных функций берутся только в некоторых частных случаях. Основным приемом интегрирования является отыскание таких подстановок, которые приводят подынтегральное выражение к рациональному виду.

Нахождение простейших интегралов вида ;

мы уже приводили в разделе

Рассмотрим более сложные иррациональные функции и приведем некоторые рекомендации.

. Интегралы вида , гденекоторая рациональная функция;целые числа, приводятся к интегралу от рациональной функции с помощью подстановки,, гденаименьшее общее кратное (НОК) знаменателей дробей.

. Интегралы вида , гденекоторая рациональная функция;целые числа.

C помощью подстановки ,, где(НОК) знаме-нателей дробей, указанный интеграл преобразуется в интеграл от рациональной функции.

. Интегралы более общего вида

приводятся к рациональному виду с помощью подстановки , где(НОК) знаменателей дробей.

. Интегралы вида путем выделения полного квадрата из квадратного трехчлена приводятся к табличным интегралам 20 или 22.

. Интегралы вида. Для нахождения этогоинтеграла выделяют полный квадрат их квадратного трехчлена подкоренного выражения, после чего интеграл разлагается на сумму двух интегралов.

. Интегралы вида. С помощью подстановкиэтот интеграл приводится к рассмотренному в.

. Интеграл от дифференциального бинома

,

где постоянные рациональные числа,постоянные числа, приводятся к интегралу от рациональной функции относительно новой переменной, лишь в следующих трех случаях:

1. Если целое число (положительное, отрицательное или 0), тогда данный интеграл сводится к интегралу от рациональной функции с помощью подстановки, гденаименьшее общее кратное знаменателей дробейи.

2. Если целое число (положительное, отрицательное или 0). В этом случае данный интеграл рационализируется с помощью подстановки, гдезнаменатель дроби.

3. Если целое число (положительное, отрицательное или 0). В этом случае к той же цели ведет подстановка , гдезнаменатель дроби.

Рассмотренные три случая были указаны еще Ньютоном. Эйлер, которого никто из математиков не превзошел в искусстве преобразо-ваний, безуспешно искал новые случаи интегрируемости биномиального дифференциала. Он пришел к убеждению, что эти три случая единствен-ные. Но лишь П.Л.Чебышев в 1853 году доказал утверждение Эйлера.

. Тригонометрические подстановки:

1. Если интеграл содержит радикал , то полагают или. Тогда

или .

2. Если интеграл содержит радикал , то полагают ,

.

3. Если интеграл содержит радикал , то полагают ,

.