
Вказівки до лаб_2010
.pdfУКООПСПІЛКА ЛЬВІВСЬКА КОМЕРЦІЙНА АКАДЕМІЯ
ТЕОРІЯ ЙМОВІРНОСТЕЙ ТА МАТЕМАТИЧНА СТАТИСТИКА
Методичні вказівки до виконання лабораторних робіт для студентів усіх напрямів підготовки
ЛЬВІВ Видавництво Львівської комерційної академії
2010
Уклали: доц. Кісілевич О. В., ст. викл. Стефаняк В. І., ас. Осміловська Н.В.
Відповідальний за випуск: проф. Копич І. М.
Рекомендовано до друку Вченою радою факультету менеджменту
Протокол № 9 від 29. 06. 2010 р.
© Кісілевич О. В., Стефаняк В. І., Осміловська Н. В., 2010 р.
|
Зміст |
|
Передмова............................................................................................................ |
|
4 |
Лабораторна робота № 1. Статистичні функції редактора Excel................ |
7 |
|
Лабораторна робота № 2. |
Вибірки з дискретно розподіленими ознаками |
|
та їх характеристики……................................................................................... |
20 |
|
Лабораторна робота № 3. |
Вибірки з неперервно розподіленими ознака- |
|
ми та їх характеристики..................................................................................... |
|
29 |
Лабораторна робота № 4. Точкові та інтервальні оцінки параметрів роз- |
|
|
поділу ................................................................................................................ |
|
39 |
Лабораторна робота № 5. Перевірки гіпотези про нормальність розподі- |
|
|
лу генеральної сукупності за допомогою критеріїв χ 2 (Пірсона) та Кол- |
|
|
могорова….......................................................................................................... |
49 |
|
Лабораторна робота № 6-7. |
Парна лінійна та нелінійні регресії ................. |
60 |
Лабораторна робота № 8. |
Множинна лінійна регресія................................ |
77 |
Лабораторна робота № 9. Множинна нелінійна регресія............................ |
86 |
|
Література ......................................................................................................... |
|
92 |
3
Передмова
У сучасному суспільстві до статистичних методів проявляється підвищений інтерес як до одного з найважливіших аналітичних інструментаріїв у сфері підтримки процесів прийняття рішень. Статистикою користуються всі — від політиків, які бажають передбачити результат виборів, до підприємців, які прагнуть оптимізувати прибуток при тих чи інших вкладеннях капіталу.
Великим кроком вперед до розвитку статистичної науки послужило застосування економіко-математичних методів і використання комп’ютерної техніки при дослідженні різноманітних соціально-економічних явищ.
Стандартні статистичні методи обробки даних включені до редакторів електронних таблиць, серед яких найпоширенішим є Excel, а також до математичних пакетів загального призначення — Mathcad, MATLAB, Maple та ін. Ще більшими можливостями статистичної обробки володіють спеціалізовані паке-
ти STATISTICA, STATGRAPHICS, SPSS, E-Views тощо.
Для проведення статистичної обробки інформації табличний процесор Microsoft Excel містить у собі програмну надбудову „Пакет аналізу” („Аналіз даних”) і бібліотеку з 78 статистичних функцій.
Всі приклади, розглянуті в цій навчально-методичній розробці, реалізовані в середовищі Microsoft Excel 2000 (англ. версія).
Уредакторі електронних таблиць Microsoft Excel 2000 для зручної роботи користувачузапропоновано понад 10 категорій вбудованих функцій.
Утаблиці наведено перелік тих функцій, які можуть використовуватися для виконання лабораторних робіт.
Таблиця 1.
Англ. |
Рос. |
Результат функції |
|
Math & Trig |
(математичні функції) |
ABS |
ABS |
абсолютна величина (модуль) числа |
COMBIN |
ЧИСЛКОМБ |
кількість комбінацій Cnk |
EXP |
ЕХР |
експонента числа |
FACT |
ФАКТР |
факторіал числа |
LN |
LN |
натуральний логарифм числа |
LOG |
LOG |
логарифм числа за заданою основою |
4

|
|
Продовження таблиці 1 |
|
LOG10 |
LOG10 |
десятковий логарифм числа |
|
MDETERM |
МОПРЕД |
визначник (детермінант) матриці |
|
MINVERSE |
МОБР |
обернена до заданої матриці |
|
MMULT |
МУМНОЖ |
добуток матриць |
|
PRODUCT |
ПРОИЗВЕД |
добуток чисел масиву |
|
RAND |
СЛЧИС |
випадкове число з проміжку (0; 1) |
|
ROUND |
ОКРУГЛ |
число, округлене до заданого розряду |
|
SQRT |
КОРЕНЬ |
квадратний корінь із числа |
|
SUM |
СУММ |
сума елементів масиву |
|
SUMPRODUCT |
СУММПРОИЗВ |
скалярний добуток масивів (сума добутків ві- |
|
дповідних елементів) |
|
||
|
|
|
|
SUMSQ |
СУМКВ |
сума квадратів елементів масиву |
|
SUMX2MY2 |
СУММРАЗНКВ |
сума різниць квадратів відповідних елементів |
|
двох масивів |
|
||
|
|
|
|
SUMX2PY2 |
СУММСУММКВ |
сума сум квадратів відповідних |
елементів |
двох масивів |
|
||
|
|
|
|
SUMXMY2 |
СУМКВРАЗН |
сума квадратів різниць відповідних |
елементів |
двох масивів |
|
||
|
|
|
|
|
Statistical |
(статистичні функції) |
|
AVEDEV |
СРОТКЛ |
|
середнє лінійне відхилення |
AVERAGE |
СРЗНАЧ |
|
середнє арифметичне (середнє значення) |
CHIDIST |
ХИ2РАСП |
|
1− F (x) , де F (x) — значення функції розпо- |
|
ділу χ 2 |
||
|
|
|
|
CHIINV |
ХИ2ОБР |
|
критичне значення розподілу χ 2 |
CORREL |
КОРРЕЛ |
|
вибірковий коефіцієнт кореляції (Пірсона) |
COUNT |
СЧЕТ |
|
кількість елементів масиву |
COVAR |
КОВАР |
|
вибіркова коваріація |
EXPONDIST |
ЭКСПРАСП |
|
значення функції розподілу або густини роз- |
|
поділу для показникового закону |
||
|
|
|
|
FDIST |
FРАСП |
|
1− F (x) , де F (x) — значення функції розпо- |
|
ділу Фішера |
||
|
|
|
|
FINV |
FРАСПОБР |
|
критичне значення F-розподілу Фішера |
|
|
|
прогнозне значення залежної змінної, знайде- |
FORECAST |
ПРЕДСКАЗ |
|
не на основі лінійної регресії за методом най- |
|
|
|
менших квадратів |
FREQUENCY |
ЧАСТОТА |
|
масив інтервальних частот |
GEOMEAN |
СРГЕОМ |
|
середнє геометричне |
HARMEAN |
СРГАРМ |
|
середнє гармонійне |
KURT |
ЭКСЦЕСС |
|
наближене значення вибіркового коефіцієнта |
|
ексцесу |
||
|
|
|
|
|
|
|
масив прогнозних значень залежної змінної в |
LINEST |
ЛИНЕЙН |
|
лінійній регресії; при потребі можна знайти |
|
|
|
найважливіші показники регресійного аналізу |
5
|
|
Продовження таблиці 1 |
|
MAX |
МАКС |
найбільший елемент масиву |
|
MEDIAN |
МЕДИАНА |
медіана дискретної вибірки |
|
MIN |
МИН |
найменший елемент масиву |
|
MODE |
МОДА |
мода дискретної вибірки |
|
NORMDIST |
НОРМРАСП |
значення функції розподілу або густини роз- |
|
поділу для нормального закону |
|||
|
|
||
NORMINV |
НОРМОБР |
значення функції оберненої до функції розпо- |
|
ділу для нормального закону |
|||
|
|
||
NORMSDIST |
НОРМСТРАСП |
значення функції стандартного нормального |
|
розподілу |
|||
|
|
||
NORMSINV |
НОРМСТОБР |
значення функції оберненої до функції стан- |
|
дартного нормального розподілу |
|||
|
|
||
PEARSON |
ПИРСОН |
вибірковий коефіцієнт кореляції (Пірсона) |
|
PERMUT |
ПЕРЕСТ |
кількість розміщень Ak |
|
|
|
n |
|
RSQ |
КВПИРСОН |
вибірковий коефіцієнт детермінації |
|
SKEW |
СКОС |
наближене значення вибіркового коефіцієнта |
|
асиметрії |
|||
|
|
||
STDEV |
СТАНДОТКЛОН |
незміщена оцінка середньоквадратичного від- |
|
хилення |
|||
|
|
||
STDEVP |
СТАНДОТКЛОНП |
зміщена оцінка середньоквадратичного відхи- |
|
лення |
|||
TINV |
СТЬЮДРАСПОБР |
критичне значення t-розподілу Стьюдента |
|
(для двосторонньої критичної області) |
|||
|
|
масив прогнозних значень залежної змінної в |
|
TREND |
ТЕНДЕНЦИЯ |
лінійній регресії (при заданому масиві нових |
|
|
|
значень незалежної змінної) |
|
VAR |
ДИСП |
незміщена оцінка дисперсії |
|
VARP |
ДИСПР |
зміщена оцінка дисперсії |
|
|
Logical |
(Логічні функції) |
|
AND |
И |
кон’юнкція (логічний добуток) аргументів |
|
FALSE |
ЛОЖЬ |
заперечення логічної константи істина |
|
IF |
ЕСЛИ |
значення функції умови |
|
NOT |
НЕ |
заперечення аргумента |
|
OR |
ИЛИ |
диз’юнкція (логічна сума) аргументів |
|
TRUE |
ИСТИНА |
логічна константа істина |
6
Лабораторна робота № 1
Статистичні функції редактора Excel
Ефективна робота користувача в Excel досягається через його активну взаємодію з інтерфейсом програми за допомогою діалогових вікон.
Щоб скористатися певною функцією Excel, можна дотримуватися наступної послідовності дій:
1)за допомогою лівої кнопки миші виділити на робочому аркуші Excel одну клітинку (або діапазон клітинок), в яких бажаємо отримати результат (такі клітинки називатимемо результуючими);
2)викликати конструктор функцій одним із наступних способів:
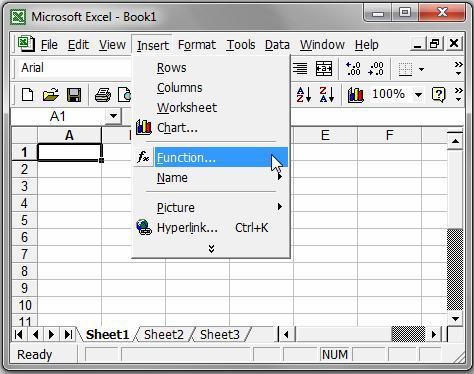
а) скористатись пунктом меню Insert → Function (рис. 1);
б) на Панелі інструментів натиснути кнопку  (рис. 2); в) у результуючій клітинці ввести символ „=” і тоді на Панелі ін-
(рис. 2); в) у результуючій клітинці ввести символ „=” і тоді на Панелі ін-
струментів у переліку доступних функцій (рис. 3) знайти More Functions…;
Рис. 1. Виклик конструктора функцій за допомогою меню Insert → Function.
7
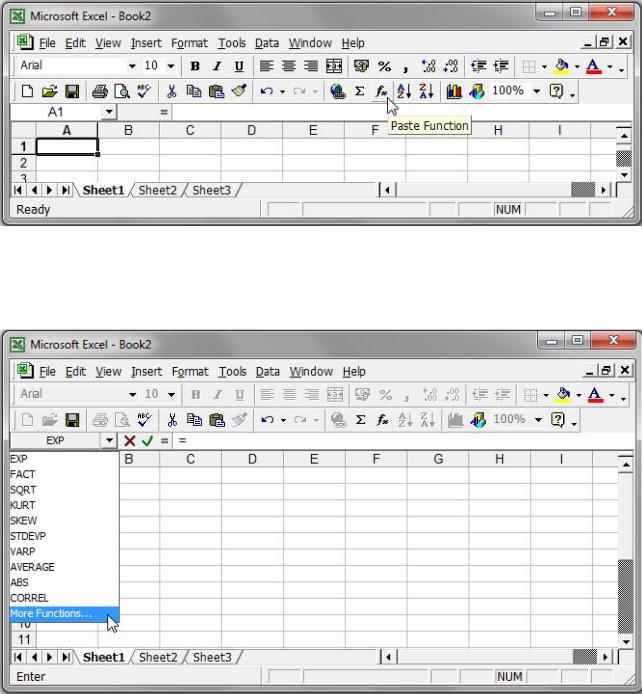
Рис. 2. Виклик конструктора функцій за допомогою кнопки fx .
Рис. 3. Виклик конструктора функцій за допомогою команди „=”.
8
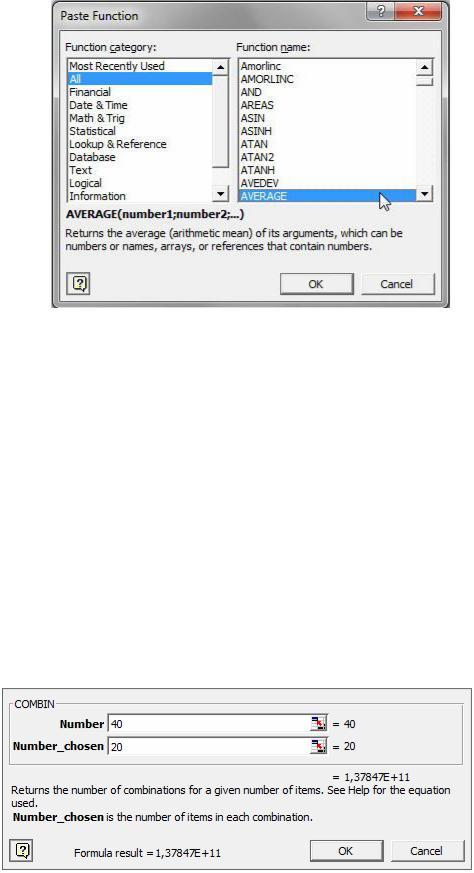
3)у діалоговому вікні, яке з’явилося (рис. 4), знайти потрібну функцію;
Рис. 4. Діалогове вікно з переліком усіх вбудованих функцій Excel.
4)у новому діалоговому вікні ввести аргументи вибраної функції і натиснути кнопку OK або клавішу Enter.
Типові завдання Завдання 1. Знайти кількість комбінацій із 40 елементів по 20.
1.Викликати конструктор функцій одним із наведених вище способів.
2.У переліку функцій знайти COMBIN.
3.У відповідному діалоговому вікні (рис. 5) ввести аргументи:
Number — число 40, Number_chosen — число 20.
Рис. 5. Діалогове вікно функції COMBIN.
9
У результуючій клітинці отримали результат 1,37847E +11 — це число,
записане у показниковому форматі і дорівнює числу 1,37847 ×1011.
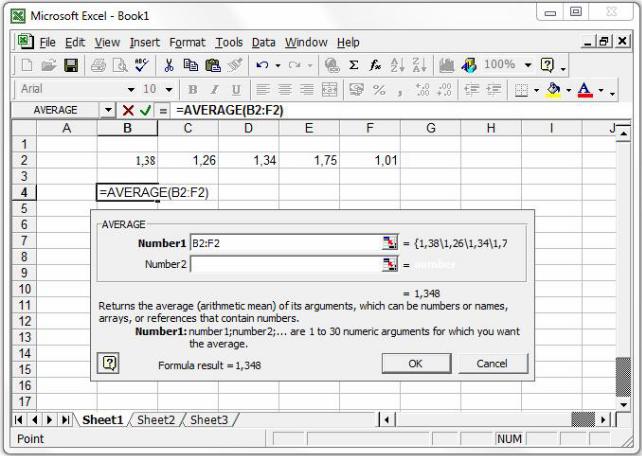
Завдання 2. Обчислити середнє арифметичне чисел: 1,38; 1,26; 1,34; 1,75; 1,01.
1.Викликати конструктор функцій.
2.У переліку функцій знайти AVERAGE.
3.У полі Number1 (рис. 6) ввести діапазон клітинок із заданим числовим масивом.
Рис. 6. Діалогове вікно функції AVERAGE.
Завдання 3. Знайти математичне сподівання дискретної випадкової величини:
xi |
1 |
3 |
7 |
8 |
9 |
pi |
0,1 |
0,3 |
0,2 |
0,3 |
0,1 |
1.Викликати конструктор функцій.
2.У переліку функцій обрати функцію SUMPRODUCT (рис. 7):
10
