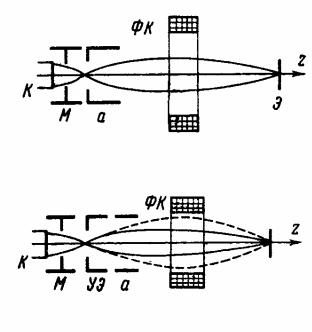
Рис. 3.11. Схемы электронных пушек с магнитной фокусировкой
Следует отметить, что благодаря сравнительно большим размерам магнитных линз они дают меньшие, чем электростатические линзы, аберрации, в результате чего хорошо фокусируются сравнительно широкие электронные пучки. Несмотря на это, такие линзы редко применяются в электронно-лучевых приборах из-за их больших габаритов, веса и потребления тока.
3.6.Отклоняющие системы
Вподавляющем большинстве электронно-лучевых приборов электронные пучки, сформированные соответствующим фокусирующим устройством, необходимо отклонить, т.е. направить на определенные участки приемника пучка. Как и для фокусировки, для отклонения электронных пучков используются электрические или магнитные поля, создаваемые соответствующими устройствами.
К отклоняющим устройствам предъявляются следующие требования: 1. Отклоняющая система должна иметь большую чувствительность. 2. Система должна обеспечивать необходимый угол отклонения пучка.
3. Искажения, вносимые в изображения отклоняющей системой, должен быть минимальным.
4. В ряде случаев требуется возможно меньшая емкость и индуктивность цепи отклоняющей системы.
На практике все эти требования в полной мере реализовать трудно и выбор типа отклоняющей системы связан с требованиями, предъявляемыми к прибору в целом.
54
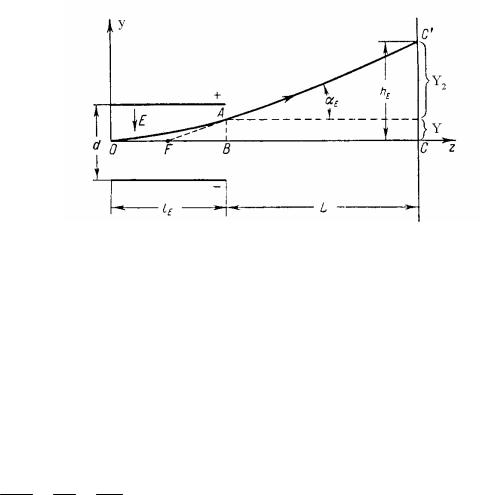
3.6.1. Электростатическое отклонение электронных пучков
Представим две параллельные пластины длиной а, расположенные на расстоянии d друг от друга и на расстоянии l от экрана (рис. 3.12).
Рис.3.12. Схема электростатического отклонения электронных пучков.
Если между пластинами приложено напряжение U, то поле плоского конденсатора, воздействуя на электроны пучка, будет отклонять их в сторону положительной пластины.
Полагая, что поле между пластинами однородно и отклоняемый пучок имеет малое поперечное сечение, можно записать, что отклонение равно:
D = Y + l ×tga (3.10)
где Y - отклонение пучка в поле пластины, a - угол отклонения, образованный осью z и направлением пучка.
Уравнение движения пучка в направлении Y имеет вид:
d2Y = eE = eU dt2 m md
Двухкратное интегрирование дает
Y = |
et2E |
+ C t + C |
2 |
|
|||
|
2m |
1 |
|
|
|
|
C1 и C2 - постоянные интегрирования,
(3.11)
(3.12)
исходя из граничных условий
равны нулю.
Подставляя в полученное выражение время нахождения электрона в поле пластины, получим для Y выражение
Y = |
а2U |
(3.13) |
|
4dUa |
|||
|
|
Для нахождения полного отклонения пучка необходимо найти угол a, тангенс которого может быть определен следующим образом:
55
|
dY |
= tga = |
|
aU |
|
|
|
(3.14) |
|
|
|
2dUa |
|
|
|
||||
|
dZ |
|
|
|
|
|
|||
Тогда из уравнения (10) |
|
|
|
||||||
D = L |
a × U |
|
|
|
|
|
(3.15) |
||
2d × Ua |
|
|
|
||||||
|
|
|
|
|
|
|
|||
где L - расстояние от экрана до точки в середине отклоняющего поля, |
|||||||||
называемой обычно центром отклонения. |
|
|
|||||||
Отклоняющее |
действие |
пластин |
обычно |
характеризуется |
|||||
чувствительностью (величиной отклонения, приходящейся на 1 В отклоняющего напряжения). Чувствительность параллельных пластин
s = |
D |
= |
L ×a |
(3.16) |
|
U |
2d × Ua |
||||
|
|
|
Величина s, очевидно, характеризует не только сами пластины, но и конструкцию всего прибора.
Полученные выражения позволяют сформулировать некоторые общие закономерности электростатического отклонения.
1.Чувствительность электростатического отклонения не зависит от заряда и массы частицы.
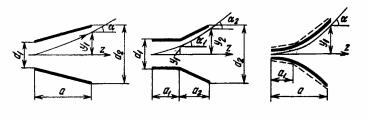
2.Чувствительность обратно пропорциональна ускоряющему анодному напряжению. Параллельные пластины - самый простой вариант электростатического отклонения, но они не могут обеспечить достаточный угол отклонения при приемлемой чувствительности. Поэтому на практике часто применяют более сложные конструкции отклоняющих пластин (рис. 3.13) для которых могут быть получены соответствующие уравнения.
Рис. 3.13. Конструкции отклоняющих пластин
3.6.2.Магнитное отклонение электронных пучков
Вслучае магнитного отклонения используются однородные взаимно перпендикулярные поля, создаваемые двумя парами обтекаемых током отклоняющих катушек (рис. 3.14).
56
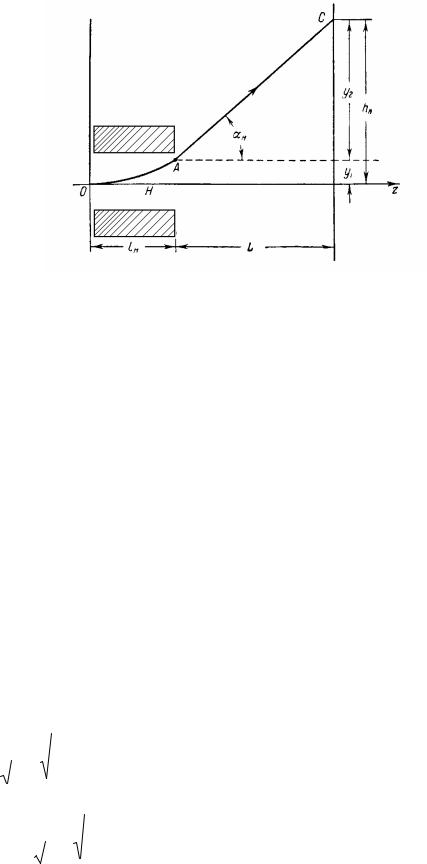
Рис. 3.14. Схема магнитного отклонения электронных пучков.
Электрон, попавший в магнитное поле, будет испытывать силу, действующую вдоль оси Y вверх и отклоняться в этом направлении, двигаясь по окружности. Радиус этой окружности выражается формулой
R = |
mv |
|
(3.17) |
|
eB |
||||
|
|
|||
При выходе из области действия поля электрон, отклонившись на |
||||
некоторую величину Y, будет |
двигаться по прямой, направленной под |
|||
некоторым углом a по отношению к оси z, и полное отклонение на экране, как и в случае электрического поля, можно будет записать в виде
D = Y + l ×tga |
(3.18) |
Из рисунка следует, что Y = R - R cosa, и если a мало, то
Y = R×a2/2 и a = sina = tga = a/R. (3.19)
Подставляя это в выражение для полного отклонения луча можно получить
|
aeBæ a |
ö |
|
aeBL |
|
||
D = |
|
ç |
|
+ l÷ |
= |
|
(3.20) |
|
2 |
vm |
|||||
|
mv è |
ø |
|
|
|||
где L = а/2 + l - расстояние от центра отклонения до экрана. Выражая скорость электрона через ускоряющее напряжение, найдем:
D = |
aLB |
|
|
e |
|
(3.21) |
|
|
|
|
|
2m |
|||
|
Ua |
|
|
||||
|
|
|
|
|
|
||
Чувствительность магнитного отклонения может быть определена как:
s = |
D |
= |
aL |
|
|
|
e |
|
(3.22) |
|
B |
|
|
|
|
|
2m |
||||
|
Ua |
|
|
|
||||||
|
|
|
|
|
|
|
|
|||
Основные закономерности магнитного отклонения:
1. Чувствительность при магнитном отклонении зависит от заряда и массы частиц.
57