f_5y40we-arphclqbl0c

71

6.3. Линейная цепочка атомов

Рассмотрим вначале линейную бесконечную цепочку одинаковых атомов, разделенных расстоянием d, фрагмент которой изображен на рис.6.1а.

Это одномерный аналог кристалла, элементарной ячейкой является отрезок цепочки длиной d. Пусть атомы имеют только одну степень свободы: они могут смещаться только вдоль цепочки. Поскольку на элементарную ячейку приходится только один атом, мы опустим индекс s (индекс j пропадает из-за наличия только одной степени свободы). Тогда уравнение (6.10) примет вид

причем в силу одномерности задачи l=dn, h=dm, где n и m – целые числа.

а

б

Рис.6.1. Фрагмент одномерной цепочки атомов, состоящей из атомов одного (а) и двух (б) сортов

где u0=ul при l=0. Конечно, величины ul должны быть вещественными. На самом деле, имеется в виду действительная часть выражения (6.14). Однако при проведении вычислений удобнее пользоваться комплексной экспонентой, а затем взять действительную часть получившегося решения.

После подстановки этого выражения в (6.13) получаем

72

Сумма, стоящая в правой части (6.15), представляет собой одномерное Фурье-преобразование функции G(h) и обозначается G(k). В силу четности G(h) (см. стр. 70) функция G(k) также является четной. Действительно

G (k ) = ∑G (h)exp(ikh ) = ∑G (−h)exp(ikh ).

Совершая замену переменных h → -h, получаем

G (k ) = ∑G (h)exp(−ikh ) =G (−k ).

h

Нетривиальное (u0≠0) решение уравнения (6.15) имеет место тогда, когда

Таким образом, условие существования нетривиального решения позволяет определить зависимость собственной частоты колебаний атомов от волнового вектора. Зависимость ω(k) называется законом дисперсии колебаний.

Кроме того, G(k=0)=0, так как при k=0 из (6.14) следует, что все ul одинаковы: происходит сдвиг всей атомной цепочки как целое без изменения расстояний между атомами. Поэтому никаких результирующих сил, действующих на атомы в новых положениях равновесия, не возникает, и правая часть уравнения (6.13) должна равняться нулю. Но величины ul=u0≠0 и, следовательно,

∑G (h) =G (k = 0) = 0 .

h

В силу четности функции G(k) оказывается, что при малых k G(k) k2 и

где s=const есть скорость продольной звуковой волны, распространяющейся по цепочке. Колебания, закон дисперсии которых имеет вид (6.17) при k→0, называют акустическими. Употребляя термин "малые k", мы не указали, по сравнению с чем. Величины

73

G(h) существенно отличны от нуля для h ≤ r0 . где r0 - радиус взаимодействия атомов в цепочке. Поэтому значения k, много меньшие 2π/r0, можно считать малыми и разлагать экспоненту в (6.15) по степеням k.

В частности, в случае взаимодействия с ближайшими соседями, когда каждый из атомов можно условно считать связанным пружинками с жесткостью κ c ближайшими к нему атомами, r0=d, а сила, действующая на атом в ячейке l со стороны правого атома, равна

F+ = κ(ul +1 −ul ),

где (ul +1 −ul ) - удлинение пружинки.

Аналогично, сила, действующая со стороны левого соседа, равна

F−= κ(ul −1 − ul )

При малых k ω(k)≈d(κ/M)1/2k, следовательно s=d(κ/M)1/2. Вид закона дисперсии ω(k) приведен на рис. 6.2.

ω

Рис.6.2. Закон дисперсии продольных акустических волн в линейной цепочке из одинаковых атомов

74

Легко видеть, что при малых k групповая vгр = dω / dk и фазовая vф = ω / k скорости волн совпадают и равны s. При k=π/d

vгр=0, а vф=2s/π.

Мы получили периодическую зависимость ω(k) с периодом 2π/d. И это не случайно. Поскольку l=nd, где n - целое число, а

ul =u0 exp(ikdn − iωt ) ,

то изменение k на величину 2π/d не приводит к изменению ни одного из смещений ul. То есть волны, для которых k отличаются на g=2πm/d, где m - целое число, неразличимы. Отметим, что g является вектором одномерной решетки, обратной по отношению к нашей цепочке.

По аналогии с проведенным рассмотрением можно сформулировать принцип, справедливый для решеток любой размерности: в дискретной периодической среде волновой вектор определен с точностью до вектора обратной решетки.

Поэтому k выбирают обычно в пределах первой зоны Бриллюэна (в нашем случае -π/d<k≤π/d ).

В заключение данного раздела рассмотрим еще один вопрос. Предшествующее изложение было проведено для бесконечной цепочки. Что изменится, если мы ограничим ее размеры? Очевидно, что вблизи оборванных концов цепочки колебания будут происходить не так, как в середине. Для исключения этих граничных эффектов замкнем концы цепочки. Пусть в ней N атомов. Тогда условие замыкания имеет вид

uN = u0

и называется периодическим граничным условием БорнаКармана.

где j - целое число.

75

Эти значения kj соответствуют собственным модам замкнутой ограниченной цепочки.

Полное число колебательных мод можно получить, разделив размер зоны Бриллюэна 2π/d на расстояние между kj, отвечающим соседним модам, равное 2π/dN Их число равно N, то есть совпадает с числом степеней свободы атомов в цепочке. Это равенство числа степеней свободы атомов и числа колебательных мод сохраняется и при переходе к многомерным кристаллическим решеткам.

6.4. Двухатомная линейная цепочка

Рассмотрим теперь цепочку чередующихся атомов двух сортов (рис.6.1б), разделенных расстоянием d/2 (d - размер элементарной ячейки для такой цепочки). Ограничимся учетом взаимодействия ближайших соседей, соответствующую жесткость обозначим κ. Пусть М1 и М2 - массы атомов разных сортов, причем М2>M1, a u1,l и u2,l - их смещения. Тогда, аналогично

(6.17), получаем

где u1,0 и u2,0 - амплитуды смещений, а l и l+d/2 - координата атомов соответствующего сорта в l-ой элементарной ячейке.

Подставляя (6.21) в (6.20), получаем

76

Условие существования нетривиального решения системы двух линейных уравнений (6.22) имеет вид

Отсюда следуют два закона дисперсии для колебаний атомов цепочки:

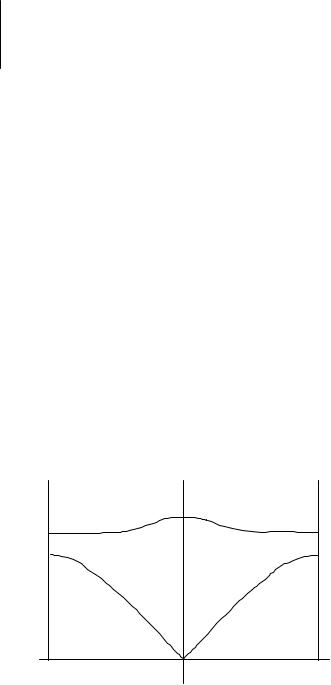
акустическим (А) и оптическим (О) колебаниям. Графически эти зависимости изображены на рис.6.3. Разлагая (6.24) при малых k, легко получить, что для k<<2π/d

ω

Рис.6.3. Законы дисперсии продольных акустических и оптических колебаний для случая двухатомной цепочки

Подставляя выражение (6.24) в одно из уравнений (6.22),

77

находим соотношение между u1,0 и u2,0 :

u1,0 =u2,0 , то есть при k=0 цепочка смещается как единое целое. В то же время для оптических колебаний при k→ 0

То есть атомы одного сорта смещаются одинаково, смещение атомов разного сорта происходит в разные стороны так, чтобы центр масс элементарной ячейки оставался бы на месте.

В ионных кристаллах, где атомы разного сорта заряжены противоположно, при таком смещении возникает дипольный момент и колебания сильно взаимодействуют с электромагнитными волнами. Именно поэтому они получили название оптических.

Отметим, что число различных типов колебаний (два), называемых ветвями, совпадает с числом степеней свободы атомов в элементарной ячейке, а число различных значений k ограниченной цепочки совпадает с числом элементарных ячеек в ней.

6.5. Трехмерные кристаллы

Пусть в элементарной ячейке трехмерного кристалла имеется n атомов. Тогда число их степеней свободы равно 3n (каждый атом, как материальная точка, имеет три степени свободы). Следовательно, существует 3n ветвей колебаний. Три из них являются акустическими, так как в трехмерном пространстве существуют три независимых направления, по которым можно сместить кристалл как целое. Остальные 3n-3 ветви являются оптическими. В частности, в кристалле с одним атомом на элементарную ячейку существуют только акустические ветви колебаний.

Рассмотрим кристалл в виде прямоугольного параллелепипеда с размерами L1, L2, L3, стороны которого параллельны кристаллографическим осям. Тогда, используя условия Борна-

78

Кармана, получаем разрешенные значения компонент волнового вектора

где j, p, q - целые числа.

Если изображать точки, задаваемые условием (6.28), в обратном пространстве, то они образуют решетку с элементарной ячейкой, объем которой равен

V 0 = (2π)3 / L1L2L3 = (2π)3 /V ,

где V - объем кристалла. На каждую такую ячейку приходится одна мода колебаний. Число мод колебаний, приходящихся на некоторый объем Ω в пространстве волновых векторов, равно

Полное число мод, отвечающее одной ветви колебаний, можно найти, распространив интегрирование на всю зону Брил-

люэна, объем которой равен (2π)3 / vяч, где vяч - объем элементарной ячейки в прямом пространстве:

N мод =V / vяч = N .

Здесь N - число элементарных ячеек в кристалле. Полное число мод равно произведению числа ветвей 3n на число мод для одной ветви N:

Nполн = 3nN

и совпадает с числом степеней свободы атомов кристалла. Вернемся теперь к решению системы дифференциальных

уравнений (6.10)

80

выражение для корней которого является достаточно громоздким. Для n≥2 аналитическое решение уравнения (6.36) в общем виде отсутствует, и его корни могут быть найдены только численными методами.

Подставив найденное значение ωp (k ) в (6.34), можно определить собственные векторы usj , то есть выразить все остальные компоненты через u11 (или любую другую компоненту). Сама же

величина u11 может быть задана произвольно. Для определенности вводят нормированные собственные векторы, обозначаемые esj ( p,k ) . Условия нормировки имеют вид

Векторы esj ( p, k ) называют векторами поляризации. Вектор поляризации показывает, как и куда смещается атом сорта s в вол-

не с волновым вектором k , относящейся к ветви под номером р. Обсудим одно важное свойство получившихся решений.

Как отмечалось в конце параграфа 6.2, уравнения движения инвариантны относительно комплексного сопряжения и изменения знака времени. Проведение обеих этих преобразований в (6.31)

эквивалентно замене k на −k . Таким образом, уравнения (6.34) должны быть инвариантны относительно такой замены. Для этого необходимо и достаточно, чтобы динамическая матрица

Dssjj'' (k ) была четной функцией волнового вектора. Но тогда чет-

ными функциями волнового вектора должны быть полученные из (6.34) законы дисперсии ωp (k ) и векторы поляризации esj ( p,k ) .

Определив собственные частоты и найдя векторы поляризации, мы тем самым определили соотношение между амплитудами и фазами колебаний атомов в волне. Однако в силу линейно-