
- •ЛАБОРАТОРНЫЕ РАБОТЫ
- •УЧЕБНО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ
- •Основная литература
- •Название, библиографическое описание
- •Дополнительная литература
- •Энергетический спектр и волновые функции электронов и дырок в полупроводниковых гетероструктурах
- •Приближение эффективной массы
- •Обезразмеривание уравнения Шредингера
- •Структуры с одиночной и множественными квантовыми ямами
- •Сверхрешетки

Структуры с одиночной и множественными квантовыми ямами
Данная задача решается в координатном представлении. Рассматривается потенциал в виде прямоугольной ямы. Оператор кинетической энергии, пропорциональный k2 (рис. 15), рассматривается как периодическая функция, Фурье-образ которой
|
|
∆z |
π / ∆z |
ik(z |
−z ) |
|
2 |
|
T |
= |
|
∫ |
T(k) e |
m n |
dk , T(k ) k |
|
. |
2π |
|
|||||||
m,n |
|
−π / ∆z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В этом случае гамильтониан системы принимает вид
Hm,n =Tm,n +U (zm )δm,n ,
а уравнение Шредингера
∑Hm,nψn = Eψm . n
Это уравнение решается методом нахождения собственных чисел (энергия) и собственных векторов (волновые функции) матрицы гамильтониана.
Структура с множественными квантовыми ямами рассчитывается, исходя из структуры с одиночной квантовой ямой посредством добавления соответствующих потенциалов.
|
Т |
|
k |
Рис. 1.5. Пе- |
риодическое |
|
продолжение кинетической энергии |
Сверхрешетки
В данной задаче рассматривается сверхрешетка на основе гетероструктуры AlxGa1-xAs/GaAs. В твердом растворе с изменением х меняются такие параметры:
1.ширина запрещенной зоны
Eg (x) =1,5194 +1,36 x +0,22 x2 эВ;
2.эффективная масса электронов
me *(x) =(0,0665+0,0835 x)m0 ,
где m0 =9,1091 10-31 кг – масса покоя электрона;
86
3. параметры Латтинджера, через которые рассчитывается эффективные массы легких и тяжелых дырок. В данной задаче нам достаточно первых двух параметров
γ1(x) =6,98−3,22 x,
γ2 (x)=2,06−1,24 x.
Через данные параметры эффективные массы легких и тяжелых дырок выражают-
ся:
mlh * (x) = |
|
m0 |
|
|
- для легких дырок, |
||
γ1(x)+γ2 (x) |
|||||||
|
|
|
|||||
mhh * (x) = |
|
|
m0 |
|
|
- для тяжелых дырок. |
|
γ1 |
(x)−γ2 |
(x) |
|||||
|
|
||||||
Задача решается в К-представлении. Потенциальная энергия представляет собой периодически повторяющуюся прямоугольную яму, образованную разрывами зон проводимости для электронов и валентных зон для дырок
∆E = |
Eg (x)−Eg (0) |
, |
|
||
c |
1+b |
|
|
|
∆Ev =b ∆Ec ,
где b = 33 – экспериментальный параметр. |
|
|
|
|
|
|
|
|||
67 |
|
|
|
|
|
|
|
|
|
|
Переход потенциала к k-координатам производится с помощью Фурье- |
||||||||||
преобразования |
|
|
|
|
|
|
|
|
|
|
|
1 a / 2 U (z) e−i |
2π |
||||||||
Um,n = |
|
|
(m−n)zdz . |
|||||||
|
a |
|||||||||
|
a −a∫/ 2 |
|
|
|
|
|
|
|
||
Тогда гамильтониан такой системы будет иметь вид |
||||||||||
|
2 |
|
|
2π |
|
|
2 |
|||
Hm,n (k) = |
|
|
k+ |
|
|
|
m δm,n +Um,n |
|||
2m |
|
|
a |
|
||||||
|
* |
|
|
|
|
|
||||
Волновая функция |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
ψ(x) = |
|
i k+ |
|
m x |
A (k) . |
|||||
∑e |
|
a |
|
|
||||||
m
m
Уравнение Шредингера в К-представлении
∑Hm,n (k)An (k)=E(k)Am (k) .
n
Уравнение решается таким же способом, как и в координатном представлении. Разница лишь в том, что для построения графиков необходим переход от К- к Х- координатам.
Указания к выполнению работы
87
1.Определить влияние изменения ширины прямоугольной потенциальной ямы на положение энергетических уровней и вид волновых функций.
2.Определить влияние изменения расстояния между прямоугольными потенциальными ямами на положение энергетических уровней и вид волновых функций.
3.Увеличивая число ям, проследить, как постепенно формируются три нижние зоны разрешенных значений энергии.
4.Меняя параметры сверхрешетки, определить их влияние на положение энергетических уровней и вид волновых функций.
88

Приложения к лабораторной работе 1
89

90

91

92

93

Лабораторная работа 2 ИССЛЕДОВАНИЕ РЕЗОНАНСНОГО ТУННЕЛИРОВАНИЯ ЭЛЕКТРОНОВ
ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЕ БАРЬЕРЫ
Цель работы: изучение эффекта резонансного туннелирования электронов через прямоугольные потенциальные барьеры, определение резонансных значений энергии туннелирования.
Теоретические сведения
При анализе всевозможных кинетических явлений в гетероструктурах часто возникает необходимость определения коэффициентов прохождения и отражения электронов и дырок, распространяющихся в направлении перпендикулярном плоскостям интерфейсов. Определение этих коэффициентов сводится к расчёту волновых функций непрерывного спектра.
Рассмотрим одномерное движение электронов (дырок) в произвольном потенциальном поле U (z), зависящем от геометрии гетероструктуры, величины разрыва зон, а также внешних электрических полей. Для простоты будем рассматривать невырожденную зону Γ1 и пренебрежём интерфейсными поправками. Соответствующее эффективное уравнение Шредингера имеет вид:
− 2 d 2F2(z)+U (z)F (z)= EF (z) 2m dz
Разобьем рассматриваемое одномерное пространство на р+1 областей шириной ∆z (рис. 1). Присвоим каждой области номер n, если она располагается в промежутке между координатами zn и zn+1.
∆z
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
z |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
1 |
z2 |
z3 |
z4 |
zp |
zp+1 |
|||||||||
Рис. 1. Схема дискретизации одномерного пространства
Если ∆z достаточно мало, то в каждой из областей потенциал U (z) можно считать постоянным и равным U (zn ), где zn = n∆z . Решение уравнение Шредингера
94

для огибающей функции F (z) и её производной F′(z) в n-ой области пространства при заданной энергии Е имеет вид:
Fn (z)= An cos kn (z − zn ) + Bn sin kn (z − zn ) ,
Fn′ (z)= kn {−An sin kn (z − zn ) + Bn cos kn (z − zn ) }, где kn = 
 2m E −U (zn ) / .
2m E −U (zn ) / .
Аналогично для n+1 области получим:
Fn+1 (z)= An+1 cos kn+1 (z − zn+1) + Bn+1 sin kn+1 (z − zn+1) ,
Fn′+1 (z)= kn+1{−An+1 sin kn+1 (z − zn+1) + Bn+1 cos kn+1 (z − zn+1) }.
Волновые функции и их производные на границе этих областей, т.е. в точке zn+1, должны удовлетворять граничным условиям:
Fn+1 (zn+1)= Fn (zn+1),
Fn′+1 (zn+1)= Fn′ (zn+1).
Отсюда следует, что
An+1 = An cos[kn∆z]+ Bn sin[kn∆z],
kn+1Bn+1 = kn {−An sin[kn∆z]+ Bn cos[kn∆z]}
Введя обозначение knBn = Cn , получим следующую матричную связь между к о- эффициентами А и С в двух областях:
An+1 |
|
= T |
An . |
|
C |
|
n C |
|
|
n+1 |
|
|
|
n |
Здесь: |
|
|
|
|
|
cos(kn∆z) |
1 |
sin (kn∆z) |
|||||||
Tn = |
|
|||||||||
|
|
sin (k |
|
∆z) |
kn |
|
∆z) |
|
||
|
−k |
n |
n |
cos(k |
n |
|
||||
|
|
|
|
|
|
|
|
|||
- матрица переноса из слоя n в слой n+1. Аналогичным образом можно получить, что:
An+2 |
|
= T |
An+1 |
|
= T T |
An . |
|
C |
|
n+1 |
C |
|
n+1 n C |
|
|
n+2 |
|
|
n+1 |
|
|
|
n |
95

Следовательно, волновая функция и её производная могут быть определены в любой наперёд заданной области с номером n, если заданы их значения в области с n=0, т.е.
An |
= T |
T |
A0 |
|
= T (n) A0 |
|
C |
n−1 |
0 |
C |
|
C |
|
n |
|
|
0 |
|
0 |
|
где
T (n) = ∏1 Tm−1 m=n
Рассмотрим единичный поток электронов с энергией Е, распространяющийся в положительном направлении оси z и падающий на гетероструктуру, расположенную в области между точками z1 и z p−1. За начало отсчёта энергии выберем значение по-
тенциала в области с n=0, т.е. положим U (z0 )= 0 . Кроме того будем считать
U (z p )≤ 0 так, что часть потока может беспрепятственно туннелировать через гете-
роструктуру, не отразившись от её гетерограниц. Полагая z0 = 0 , запишем решение
уравнения Шредингера в нулевой области в виде суммы двух волн: падающей с ампл и- тудой, равной единице, и отражённой:
F0 (z)= eik0z + re−ik0z ,
F0′(z)= ik0 eik0z −re−ik0z
здесь r – амплитудный коэффициент отражения, k0 = 
 2m E / . Далее получа-
2m E / . Далее получа-
ем:
A0 =1+ r
C0 = ik0 (1−r)
Решение в р-ой области должно иметь вид прошедшей волны:
Fp (z)= t |
|
k0 |
|
eik pz , |
|
||||
|
|
k p |
||
Fp′ (z)= it
 k0k p eik0z
k0k p eik0z
где t – амплитудный коэффициент прохождения. Далее находим:
96

|
|
k0 |
|
ik pzp |
|
|
Ap = |
|
e |
t, |
|||
k p |
||||||
|
|
|
|
|
||
Cp = i
 k0k p eik pzp t,
k0k p eik pzp t,
где z p = p∆z . С другой стороны элементы столбца A0 , C0 и Ap , Cp связаны между собой матричным уравнением:
Ap |
= T ( p) |
A |
|
T ( p) |
T ( p) |
A |
|
|||||
|
C |
|
|
0 |
|
= |
11 |
12 |
|
0 |
|
|
|
p |
|
|
C |
|
|
( p) |
( p) |
|
C |
|
|
|
|
0 |
T21 |
T22 |
0 |
|||||||
|
|
|
|
|
|
|
|
|
|
|||
где T ( p) = ∏1 Tm−1 , которое позволяет выразить коэффициенты r и t через матрич- m=p
ные элементы матрицы переноса Tij( p) :
r = −k pT11( p) −ik pk0T12( p) −iT21( p) +k0T22( p) k pT11( p) −ik pk0T12( p) +iT21( p) +k0T22( p)
2 k pk0 (T ( p)T ( p) −T ( p)T ( p) )
t = 11 22 12 21 e−ik p p∆z k pT11( p) −ik pk0T12( p) +iT21( p) +k0T22( p)
Полученные формулы позволяют вычислить r и t как функции энергии падающих электронов Е и определить коэффициенты отражения R (E)= r (E)2 и прохождения T (E)= t (E)2, удовлетворяющие условию R (E)+T (E)=1.
Указания по выполнению работы
1.Меняя параметры потенциального барьера исследовать эффект туннелирования электронов через одиночный потенциальный барьер.
2.Изменяя параметры потенциальных барьеров, найти оптимальное отношение параметров для наибольшей вероятности туннелирования электронов.
3.Сделать выводы о проделанной работе.
97

Приложения к лабораторной работе 2
98
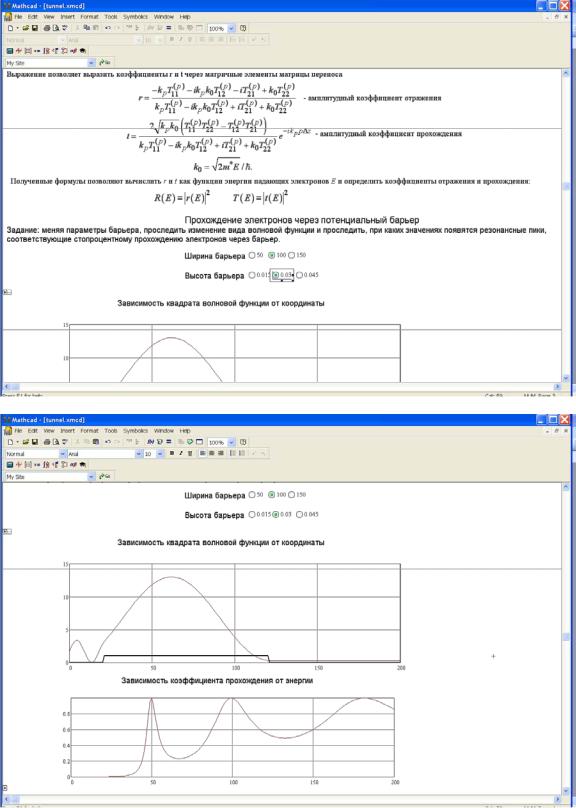
99

100

Лабораторная работа 3 ЕМКОСТНАЯ ДИАГНОСТИКА ПОЛУПРОВОДНИКОВЫХ КВАНТОВО-
РАЗМЕРНЫХ СТРУКТУР
Цель работы: получение представлений о емкостном методе исследования кван- тово-размерных структур, определение их наличия в исследуемом образце по виду вольт-фарадной характеристики.
Основные сведения
Приборы современной наноэлектроники создаются на базе сложных многослойных полупроводниковых гетероструктур, в состав которых могут входить десятки нанометровых слоев. Одним из важнейших критериев качества наноструктуры является правильность ее функционирования, что обеспечивается соответствием реальной и расчетной электронных систем структуры с гетеропереходами.
В этой работе исследуется метод емкостной диагностики. Он позволяет осуществлять неразрушающий контроль качества квантово-размерных структур. Диагностика структуры заключается в определении по вольт-фарадным характеристикам ее электрофизических параметров, таких как распределение концентрации свободных носителей заряда и легирующей примеси, положение энергетических уровней квантования, разрыв энергетических зон и др.
Рассмотрим типичную C-V-характеристику гетероструктуры с квантовой ямой (рис. 1, а) в координатах C-2(V). На ней наблюдается почти горизонтальное плато в определенном диапазоне обратных напряжений ,что является характерным признаком наличия квантовой ямы или слоя квантовых точек. Причина появления плато объясняется тем, что увеличивающаяся с приложенным смещением область объемного заряда пересекает своей границей область обогащения основными носителями заряда, связанную с
а) |
б) |
Рис. 1. Вольт-фарадная характеристика (а) и распределение концентрации (б) в
изотипной гетероструктуре с квантовой ямой InxGa1-xAs/GaAs (0.065<x<0.3)
квантовой ямой. Вблизи границ квантовой ямы наблюдается снижение концентрации (рис. 1, б), т.е. существует область, обедненная носителями, ушедшими в квантовую яму. Размер этой области примерно оценивается дебаевской длиной экранирования:
101

где - диэлектрическая проницаемость, n – концентрация подвижных носителей. Барьерная емкость гетероперехода определяется исходя из формулы :
где n – концентрация свободных носителей, V – изгиб зон (включает встроенный потенциал и приложенное смещение). Дифференцирование этой зависимости позволяет получить формулу для распределения концентрации по глубине образца x (S – площадь перехода):
где x определяется из формулы плоского конденсатора:
Метод обладает высокой чувствительностью к изменению заряда, и поэтому возможно чувствительное измерение разрывов зон и ширины квантовых ям. Однако это требует достаточно сложного численного моделирования вольт-фарадных характеристик с учетом многих эффектов, таких как пространственное ограничение (связано с соотношением размеров квантовых ям и де-бройлевской длины волны носителей).
Измерительная установка
В качестве измерительного устройства используется измеритель иммитанса МНИПИ Е7-20. Внешний вид прибора приведен на рис. 2.
Рис. 2. Внешний вид измерителя иммитанса МНИПИ Е7-20
Иммитанс – термин, объединяющий понятия адмиттанса (Y, комплексной проводимости) и импеданса (Z, комплексного сопротивления). Уравновешивание измерительной (мостовой) схемы в приборе осуществляется одновременно по емкостной и активной составляющим Y:
102

 Θ G
Θ G
|Y|
 jB
jB
Рис. 3. Векторное представление комплексной проводимости
где G – активная часть адмиттанса – проводимость (conductance); В – емкостная часть (susceptance); R – сопротивление; С – емкость. Величина обратная адмиттансу, импеданс Z, также имеет активную и емкостную части.
В основу работы прибора положен метод вольтметра-амперметра. Структурная схема приведена на рис. 4. Напряжение рабочей частоты от генератора подается на измеряемый объект. Преобразователь формирует два напряжения, одно из которых Uт пропорционально току, протекающему через образец, а другое Uн – напряжению на нем. Отношение этих напряжений равно комплексной проводимости Y или комплексному сопротивлению Z.
Измерение отношения напряжений производится аппаратно-программным лого-
|
|
Коммутатор |
Масштабный |
|
Z |
усилитель |
|
|
|
||
|
|
|
|
Генератор |
Преобразователь |
|
|
|
АЦП |
|
|
Интерфейсное |
|
Контроллер |
|
устройство |
|
|
|
RS-232C |
|
|
|
|
Индикатор |
Клавиатура |
|
Рис. 4. Структурная схема измерителя иммитанса МНИПИ Е7-20
метром. Аппаратная часть логометра состоит из коммутатора, масштабного усилителя и аналого-цифрового преобразователя (АЦП). Программная часть производит расчет отношений напряжений.
103

На рис. 5 изображены векторы Uн, Uт и опорного вспомогательного напряжения с произвольной фазой. Проекции Uн и Uт на опорное напряжение Uоп и jUоп выделяются синхронным детектором и измеряются в некотором произвольном масштабе измерителем интегрирующего типа.
jUоп |
|
|
Uт (Uн) |
|
|
b |
|
|
d |
|
Uн (Uт) |
|
|
|
a |
c |
Uоп |
|
Рис. 5. Векторная диаграмма формируемых и опорных напряжений
Из соотношения
где G – активная, B – реактивная проводимости; a, b, c, d – проекции измеряемых напряжений Uн и Uт на опорное Uоп и jUоп, можно получить выражения для составляющих проводимости:
Аналогично из
где R – активное, X - реактивное сопротивления:
Интерфейсное устройство RS-232C обеспечивает возможность подключения измерителя к компьютеру (через COM-порт).
Программное обеспечение (см. рис. 6) автоматизирует процесс измерения вольтфарадных характеристик, сохраняет результаты в удобном для обработки виде. Для запуска измерений нужно ввести параметры: вид измерений, диапазон напряжений, пауза на релаксацию, усреднение, параметры измерительного сигнала.
104

Рис. 6. Внешний вид программы для автоматизации измерений
При измерении вольт-фарадной характеристики, естественно, производится изменение постоянного смещения. При этом наблюдаются переходные процессы, протекающие в измерительном приборе (перезарядка емкостей измерительного моста и т.п.), которые вызывают отклонение показаний от действительных значений. Пауза на релаксацию указывает интервал времени, к которому, как предполагается, эти переходные процессы заканчиваются. Усреднение значений позволяет в некоторой степени сгладить шум.
105

Рис. 7. Переходные процессы при изменении напряжения смещения.
106
Порядок выполнения работы
1)Включите компьютер и измеритель иммитанса.
2)Запустите программу МНИПИ Е7-20 (значок на рабочем столе). В сплывающем окне выбора порта нажмите «ОК».
3)Подключите к клеммам измерителя Образец 1 так, чтобы подаваемое на него смещение было обратным. Для проверки можно осуществить следующие действия:
•На измерителе иммитанса нажмите кнопку «I» - измерение тока;
•Справа от дисплея прибора нажмите «СМЕЩ» - режим изменения напряжения смещения;
•Нажмите несколько раз на кнопку «Стрелка вправо», установив смещение 2.5-3 В. По значению тока найдите обратное включение.
4)В программе установите режим измерения:
Вобласти «Вид измерений»:
•Измеряемая величина – Емкость;
•Доп. измерение – Проводимость;
•Зависимость – Напряжение;
•Снимите галочку с пункта «Усреднять значения»;
Вобласти «Настройка автоматических измерений»:
Диапазон напряжений:
•Начальное значение: 0 В;
•Конечное значение: 4 В;
•Пауза на релаксацию: 2 сек; Измерительный сигнал:
•Амплитуда: 0.04В;
•Частота: 1000 кГц;
5)Нажмите кнопку «Измерение». Прибор выставит необходимые параметры и начнет измерение вольт-фарадной характеристики образца.
6)По завершении измерений в главном меню программы выберите пункт «Измерения – Сохранить результат». Выделите пункт «Эксперимент № 1» и
нажмите «Сохранить». Сохранение производится в формате, поддерживаемом
MS Excel.
7)Подключите к клеммам измерителя Образец 2, чтобы на него подавалось обратное смещение (см. п. 3).
8)Аналогично п. 4 установите режим измерения, изменив следующие параметры:
•Усреднять значений: 5 (отметить галочкой этот пункт);
Диапазон напряжений:
•Начальное значение: 0 В;
107

•Конечное значение: 4 В;
•Пауза на релаксацию: 3 сек;
9)Нажмите кнопку «В серию». Измерение занесено в серию, что показано в появившемся окне. Нажмите в нем «Закрыть».
10)Снова установите параметры эксперимента (для новой серии):
•Усреднять значений: 7;
Диапазон напряжений:
•Начальное значение – 4.2 В;
•Конечное значение – 10 В;
•Пауза на релаксацию – 5 сек.
Примечание: Прибор изменяет значение смещения в разных диапазонах на разную величину (от 0 до 4 В – через 0.02 В, от 4 до 10 В – через 0.2 В). При большом шаге изменения релаксационный процессы происходят дольше.
11)Нажмите на кнопку «В серию». Теперь в появившемся окне присутствует две записи – ваши эксперименты. Нажмите в этом окне кнопку «Измерение».
12)Пока прибор выполняет снятие вольт-фарадных характеристик Образца 2, откройте в Microsoft Excel файл, созданный по результатом измерения Образца 1. На вопрос, задаваемый MS Excel ответьте «Да».
13)Постройте график вольт-емкостной зависимости в координатах C-2(V). (В соответствующие ячейки нужно ввести формулы. Например, «=B5^-2» без кавычек).
14)Пользуясь формулой распределения концентрации носителей по глубине образца:
постарайтесь качественно проанализировать полученный график. Какое распределение носителей в исследуемом образце?
15)По завершении прибором измерений (обоих экспериментов из серии) с помощью кнопок «Стрелка влево» и «Стрелка вправо» на панели прибора установите значение смещения 0В.
16)Подключите Образец 2 таким образом, чтобы на него подавались прямые смещения (поменяйте клеммы местами).
17)Выполните измерения аналогично п. 4 в диапазоне напряжений 0-2.5 В, с паузой на релаксацию 3 сек, усреднением 5 значений.
18)По окончании эксперимента сохраните результаты последних трех экспериментов (2 – в обратных смещениях, 1 – в прямом), выбрав «Измерения
– Сохранить результат». В появившемся окне выделите нужные эксперименты и нажмите «Сохранить».
108
19)Закройте программу, выключите измеритель Иммитанса.
20)Отчет должен содержать вольт-фарадную характеристику Образца 2 в исследованном диапазоне (от -10 В до 2.5 В), рассчитанный профиль концентрации. Необходимые для расчета параметры образца узнайте у преподавателя.
Примечание: анализ данных и построение профиля концентрации следует проводить в математическом пакете MathCad. Ввод измеренных данных в него осуществляется следующим образом:
•В главном меню выбрать «Insert - Component»;
•Из появившегося списка выбрать «Microsoft Excel»;
•Create from file (ввести путь к файлу);
•Inputs=0, Outputs=2, указать диапазоны ячеек, соответствующие напряжению и емкости.
•Ввести имена переменных MathCad (например, U и С).
•Для интерполяции функций можно пользоваться функциями cspline и interp (см. описание в Help).
•Численное дифференцирование проводится после сглаживания шумов. Для сглаживания удобно использовать ksmooth (см. описание в Help). Параметр b выбирается таким образом, чтобы шумы не давали значительных флуктуаций производной, а перегибы вольт-фарадной характеристики значительно не изменились.
109

Лабораторная работа № 4. МЕЛКИЕ ВОДОРОДОПОДОБНЫЕ ДОНОРНЫЕ УРОВНИ В КВАНТОВЫХ ЯМАХ
Цель работы: исследование энергетического спектра водородоподобной примеси, моделирование спектра водородоподобной примеси, находящейся в квантовой яме
AlxGa1–xAs/GaAs.
1. Теоретические сведения
1.1 Водородоподобная примесь
В лабораторной работе проводится исследование энергетического спектра водородоподобной примеси в кристаллической решетке полупродникового материала. Примесь считается
1.мелкой, то есть глубина ее залегания существенно меньше ширины запрещенной зоны образца,
2.однократно ионизованной,
3.являющейся примесью по типу замещения.
Таким образом, ионизованный электрон примеси находится в поле положительно заряженного остова, а также кристаллическом поле полупроводника. Кулоновское поле экранируется, так как между электроном и центром располагается среда. При большом радиусе связи, что справедилоиво для мелких примесей, влияние среды может быть учтено введением диэлекрической проницаемости. Пренебрегая атомным строением, можно считать ее равной макроскопической диэлекрической проницаемости ε . Можно показать [3], что боровский радиус для донора в GaAs (в СГС)
a |
|
= |
ε 2 |
= |
m0 |
|
ε a0 |
, |
a |
|
≈ |
1 |
12 0.53 10−10 м |
≈ 20 a |
D |
|
|
D |
|
||||||||||
|
|
m e2 |
|
|
B |
|
|
0.06 |
|
0 |
||||
|
|
|
|
m |
|
|
|
|
|
|
||||
составляет несколько десятков постоянных решетки a = 0.56 10−9 |
нм. Так, в объе- |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
ме, охватываемом характеристическим размером системы, находится несколько тысяч узлов кристаллической решетки, что делает правомочным введение макроскопической диэлекрической проницаемости.
Легко видеть, что кулоновский потенциал, действующий на электрон в твердом теле, выглядит как
U (x)= − e2 .
ε x
110

Рис. 4.1. Соотношение характеристического размера системы
ипостоянной решетки
1.2Метод эффективной массы
Решаем задачу в приближении эффективной массы: информация о кристаллическом потенциале включается в эффективную массу. При этом уравнение, описывающее
движение в периодическом кристаллическом потенциале Uк (x) и внешнем Vвн (x),
ˆ |
|
pˆ 2 |
|
|
|
|
|
HΨ(x)= |
2m0 |
+U |
|
(x)+V |
(x) |
Ψ(x)= EΨ(x) |
|
|
|
|
к |
вн |
|
|
|
|
|
|
|
|
|
|
|
при условии плавности потенциала Vвн (x) можно привести к уравнению эффективной массы:
|
|
2 |
2 +V |
|
|
− |
|
(x) F (x)= EF (x), |
|||
2m |
|||||
|
вн |
|
|||
|
|
|
|
|
|
где m – эффективная масса, F (x) – огибающая волновая функция. Несмотря на то, что решением нового уравнения является уже другая, не исходная Ψ(x), волновая функция, энергетический спектр En совпадает.
Применяя метод эффективной массы к нашей задаче, перейдем от уравнения Шредингера для волновой функции:
111

|
pˆ |
2 |
+U |
|
(x)− |
e2 |
Ψ(x)= EΨ(x), |
||||
|
|
|
к |
|
|
|
|
|
|||
|
|
|
x |
|
|
||||||
|
2εm0 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
к уравнению для огибающей, но с тем же спектром собственных значений энергии:
|
|
2 |
2 − |
e |
2 |
|
|
|
|
− |
|
|
|
|
F (x)= EF (x). |
||||
2m |
ε |
|
x |
|
|
||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение задачи для такого вида потенциала хорошо известно – это атом водорода. Единственным отличием является наличие диэлекрической проницаемости и эффективной массы. Таким образом, дискретный спектр мелкой водородоподобной примеси в кристаллической решетке полупродникового материала записывается, исходя из известного спектра атома водорода:
En = − Rn2 ,
где R = |
m e4 |
= |
m0e4 |
m |
|
1 |
= Ry |
m |
|
|
1 |
и Ry =13.606 эВ. |
||
|
2 2 |
2 |
m |
2 |
||||||||||
|
2ε |
2 |
|
2 |
m |
|
|
|
|
|||||
|
|
|
0ε |
|
|
|
0ε |
|
|
|
||||
1.3 Квантовая яма
Помещение донорной примеси в потенциальную яму вызывает изменение энергетического спектра. Электрон в твердом теле находится под влиянием потенциала ямы и кулоновского потенциала, создаваемого положительно заряженным остовом.
Задача о нахождении энергетического спектра электрона в потенциальной яме с бесконечно высокими стенками шириной a имеет точное решение:
En = π2 2n2 , где n = 0, 1, 2, ...
2ma2
При добавлении кулоновского потенциала уже невозможно получить точное решение и нужно использовать другие методы решения. Применение вариационного метода позволяет свести трехмерную задачу с кулоновским потенциалом к одномерной задаче с эффективным потенциалом, вдоль оси, перпендикулярной к плоскости квантовой ямы.
112

Рис. 4.2. Эффективный потенциал в направлении, перпендикулярном к плоскости квантовой ямы (для 1s-состояния)
Рис. 4.3. Эффективный потенциал в направлении, перпендикулярном
кплоскости квантовой ямы (для 2p0-состояния)
1.4Вариационный метод
Вариационный метод расчета основан на минимизации функционала, соответствующего собственной энергии системы. Данным функционалом является гамильтониан сис-
темы, взятый в обкладках неких приближенных волновых функций Fn(x) .
En = ∫ Fn (x)HFˆ n(x)dx
V
В качестве приближенных волновых функций выбираются функции, отвечающие требованиям симметрии и смыслу задачи. Чем ближе приближенная функция к точной Fn(x) , тем более точно можно получить энергетический спектр.
En = ∫ Fn (x)HFˆ n(x)dx = ∫ Fn (x)EnFn(x)dx = En ∫ Fn (x)Fn(x)dx = En
V V V
113

Значит, варьируя некий параметр a , от которого будет зависеть Fn(x)
лять степенью приближения волновых функций к точным. Следовательно, значение функционала стремится к точному значению энергии при оптимальном значении a , таком, что
∂∂a En = 0 .
Соответствующее значение ему функционала будет искомым уровнем энергии.
2. Указания к работе
Расчет исследуемых энергетических спектров производится в программе Mathcad.
Энергия выражается в естественных единицах задачи – Ридбергах R , длина – в единицах радиуса Бора задачи.
1.Включите компьютер, дождитесь загрузки операционной системы
2.Запустите Mathcad
3.Откройте указанный преподавателем файл
4.Следуйте указаниям в тексте
5.Сохраните результаты работы
6.Выйдите из Mathcad, выключите компьютер
3.Требования к отчету
Вотчете по лабораторной работе должны быть приведены:
1.Вывод единиц измерения и обезразмеривание
2.Уровней первых двух связанных состояний для мелкой водородоподобной примеси при отсутствии потенциала квантовой ямы
Для 1s: |
Для 2p0: |
3.Уровни первых двух связанных состояний для мелкой водородоподобной примеси в квантовой яме AlxGa1–xAs/GaAs, x=0,3
4.Зависимости положения энергетических уровней от ширины квантовой ямы
5.Зависимости положения энергетических уровней от глубины квантовой ямы
6.Зависимости положения энергетических уровней от сдвига примесного центра относительно середины квантовой ямы
114

Рис. 4.4. Зависимость энергии S-состояния (кривая 1) от смещения Δz донорной примеси относительно центра (середины) квантовой ямы к решению. Решение в отсутствие кулоновского поля (кривая 2). Вертикальная прямая показывает границу ямы
Вопросы
1.Почему при решении задачи о нахождении энергетического спектра мелкой водородоподобной примеси в полупроводниковом кристалле можно использовать решение задачи об атоме водорода?
2.Каковы допущения в методе эффективной массы?
3.Решение каких модельных задач можно получить в частном случае?
Список литературы
1.Драгунов В.П., Неизвестный И.Г., Гридчин В.А. Основы наноэлектроники: Учебное пособие. – М.: Университетская книга; Логос; Физмат-книга, 2006. –
496 с.
2.Ландау Л.Д., Лифшиц Е.М. Теоретическая физика: Учебное пособие для вузов. В 10 т. Т. III Квантовая механика (нерелятивистская теория) – М., Наука, 1989,
768 с.
3.Шик А.Я., Бакуева Л.Г., Мусихин С.Ф., Рыков С.А. Физика низкоразмерных систем / Под ред. А.Я. Шика. – СПб.: Наука, 2001. 160 с.
115
Лабораторная работа 5 РАСЧЕТ ЭНЕРГЕТИЧЕСКОГО СПЕКТРА И ВОЛНОВЫХ ФУНКЦИЙ ЭЛЕК-
ТРОНА В КВАНТОВЫХ ТОЧКАХ РАЗЛИЧНОЙ ФОРМЫ
Цель работы: ознакомиться со методами расчета энергитческого спектра и волновых функций электронов в квантовых точках различной формы в k- и узельном представлениях.
Основные сведения
1. Уравнение Шредингера в матричной форме
Интегральное уравнение в k-представлении в методе эффективной массы имеет
вид:
2 |
1 |
k k F(k ) + |
|
V |
(k −k ') F(k ') = E F(k ) , |
|
|
|
|
|
|||
|
i внj |
|
|
|||
2 m* i, j |
∑ |
|
|
|||
|
k ' |
|
|
|||
для изотропного материала:
2k2 |
F(k ) +∑Vвн (k −k ') F(k ') = E F(k ). |
2m* |
k ' |
В этом уравнении k является параметром, поэтому для различных k можно записать систему уравнений:
|
|
2k2 |
|
|
|
|
|
∑ |
2m* |
δkk ' +Vвн (k |
−k |
') |
F(k |
') = E F(k ) . |
|
|
|
|
|
|
|
|
|
k |
' |
|
|
|
|
|
|
В матричной форме полученная система уравнений будет являться задачей на поиск собственных чисел и собственных векторов матрицы
H |
= |
2k2 |
δ |
+V |
(k −k '). |
kk ' |
|
2m* |
kk ' |
вн |
|
Для определения потенциальной энергии Vвн (k −k ') используем Фурьепреобразование для функции, заданной в дискретных точках:
Vвн (k −k ') = ∑a Vвн(a) exp(−i(k −k ') a)
Аналогично расчету в k-представлении, можно проводить расчет в узельном представлении
∑a ' T (a −a ') F(a ') +Vвн (a) F(a) = E F(a)
116

Тогда задача сводится к поиску собственных чисел и собственных столбцов следующей матрицы:
H (a −a ') = T (a −a ') +Vвн (a)δaa '
Здесь, однако, надо производить обратное Фурье-преобразование для кинетической энергии:
T (a −a ') = ∑ 2k2 exp(ik (a−a '))
k 2m*
2. Размер расчетной области
Для бесконечного кристалла число точек x бесконечно, а k непрерывно, поэтому все матрицы бесконечны. Однако на практике для расчета обычно используют ограниченные кристаллы, и волновой вектор k принимает
дискретные значения. При этом:
•число различных значений k равно числу элементарных ячеек кристалла
•k всегда лежит в пределах зоны Бриллюэна
•дискретное k должно включаться на одной границе зоны Бриллюэна и исключаться на противоположной
На рис. 1 приведен пример расположения точек k- пространства в зона Бриллюэна. Заметно, что точки включаются на правой границе зоны Бриллюэна и исключаются на левой.
Рис. 1. Зона Бриллюэна с точками k
3. Прямая и обратная решетки
В обычно рассматриваемых кристаллах прямая решетка является кубической ГЦК решеткой. Вектора прямой ГЦК решетки имеют вид:
a1 = a20 (1 1 0) a2 = a20 (1 0 1) a3 = a20 (0 1 1),
где a0 – период решетки, a0  2 – ширина монослоя (расстояние между слоями атомов). Вид ГЦК решетки (в единицах монослоя) представлен на рис. 2.
2 – ширина монослоя (расстояние между слоями атомов). Вид ГЦК решетки (в единицах монослоя) представлен на рис. 2.
117

а) |
б) |
Рис. 2. Прямая ГЦК решетка:
а) в привычном представлении, когда атомы расположены в углах куба; б) в представлении, когда в центре куба расположен атом
Прямой ГЦК решетке соответствует обратная ОЦК решетка со следующими векторами обратной решетки:
b1 = 2aπ (1 1 1) |
|
|
0 |
|
|
b2 = 2aπ (1 1 1) |
|
|
0 |
|
|
b3 = 2aπ (1 1 1) |
|
|
0 |
|
|
Вид ОЦК решетки (в единицах 2π a0 |
) пред- |
Рис. 3. Обратная ОЦК решетка |
ставлен на рис. 3. |
|
|
|
|
4. Расположение точек k внутри расчетной области
Расчетные точки располагаются вдоль векторов обратной решетки:
|
|
|
|
|
|
m |
|
|
n |
|
|
p |
|||||||||
k |
mnp |
= k |
+k |
2n |
+k |
3 p |
k |
|
= b |
|
k |
2n |
= b |
|
|
k |
3 p |
= b |
|
|
|
|
|
N |
|
N |
|
|
|||||||||||||||
|
1m |
|
|
1m |
1 N |
|
2 |
2 |
|
3 |
3 |
|
|||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
где N1 , N2 , N3 |
– число точек вдоль соответствующих векторов обратной и прямой ре- |
||||||||||||||||||||
шеток, m = 0 N1 −1, n = 0 N2 |
−1, |
p = 0 N3 −1. |
|
|
|
|
|
|
|
|
|
|
|||||||||
118
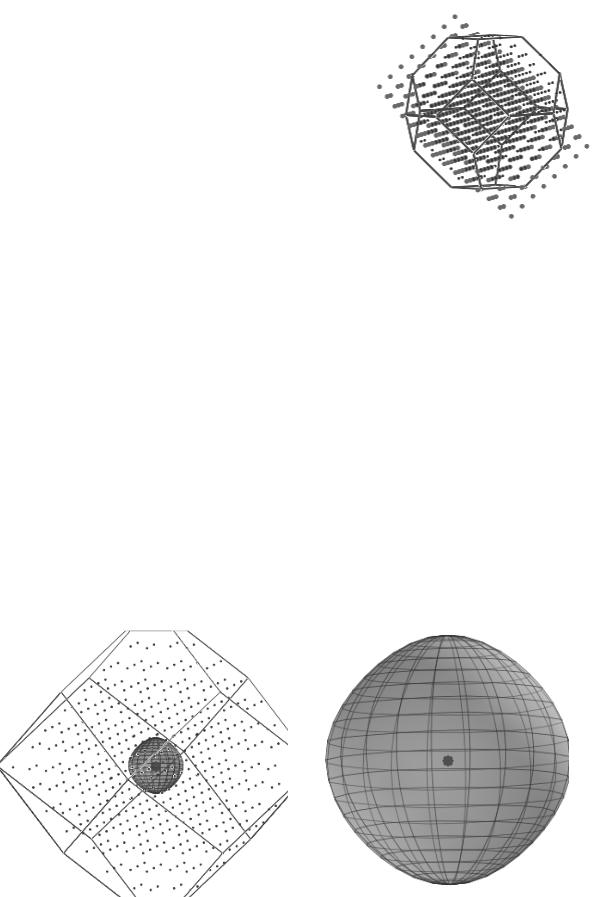
Однако, использование этих формул приводит к тому, что расчетные точки k-пространства располагаются не в зоне Бриллюэна, а в некоем косоугольном параллелепипеде (см. рис. 4). Для исправления этой ситуации используется простой алгоритм: к каждой точке последовательно прибавляются различные комбинации векторов обратной решетки, и выбирается тот результат, который лежит ближе всего к центру первой зоны Бриллюэна.
Указания по проведению работы
1.Включить компьютер, открыть файл «лаб. Раб. 5. КТ.mcd»
Расчет кубической КТ
Рис. 4. Приведение расчетных точек в зону Бриллюэна
2.Установить переключатель «вид КТ» в значение «Куб»
3.Задавая различные значения размера куба, смотреть, как от этого меняется набор энергетических уровней и волновые функции
4.Задать размер куба X0=Y0=Z0=0 и получить значения энергии и вид волновой функции для квантовой точки из одного атома: E= –4,8732
Энергии первого связанного состояния и волновая функция электрона (поверхность равных вероятностей) для квантовой точки, содержащей один атом. Здесь и далее энергия измеряется в относительных единицах.
119

5.Задать размер куба X0=Y0=Z0=1 и получить значения энергии и вид волновых функций первых девяти связанных состояний для квантовой точки из 13 атомов:
Энергии связанных состояний и волновые функции электронов (поверхности равных вероятностей) для квантовых точек кубической формы:
E= –8.142054
E= –6.333152, –6.333149, –6.333146
120

E= –4.618686, –4.618685, –4.618684
E= –3.343652, –3.343642
Расчет сферической КТ
6.Установить переключатель «вид КТ» в значение «Сфера»
7.Задавая различные значения радиусы сферы, смотреть, как от этого меняется набор энергетических уровней и волновые функции
8.Задать радиусы сферы R1=R2=0 и получить значения энергии и вид волновой функции для квантовой точки из одного атома: E= –4,8732; волновые функции совпадают с п. 4.
9.Задать радиусы сферы R1=1 R2=2 и получить значения энергии и вид волновых функций первых шести связанных состояний для квантовой точки из 18 атомов:
121
Энергии связанных состояний и волновые функции электронов (поверхности равных вероятностей) для квантовых точек сферической формы:
122

E= –7.806903
E= –6.972198, –6.972197, –6.972196
123
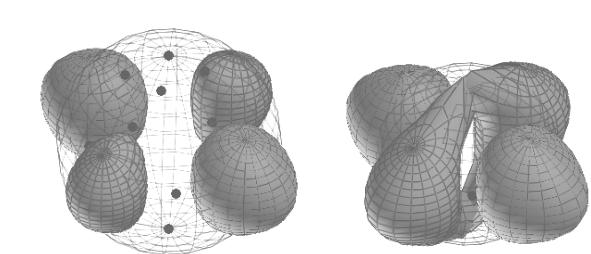
E= –5.619666, –5.619663
Расчет пирамидальной КТ
10.Установить переключатель «вид КТ» в значение «Пирамида»
11.Задавая различные значения высоты пирамиды, смотреть, как от этого меняется набор энергетических уровней и волновые функции
12.Задать высоту пирамиды H=0 и получить значения энергии и вид волновой функции для квантовой точки из одного атома: E=–4,8732; волновые функции совпадают с п. 4 и п.8.
13.Задать высоту пирамиды H=3 и получить значения энергии и вид волновых функций первых шести связанных состояний для квантовой точки из 42 атомов:
Энергии связанных состояний и волновые функции электронов (поверхности равных вероятностей) для квантовых точек пирамидальной формы:
124

E= –8.707678
E= –7.839383, –7.839382
E= –7.299672
125

E= –7.168247
E= –6.767927
126

E= –6.540472
E= –6.482579, –6.482578
127
МИНИСТЕРСТВО ОБРАЗОВ АНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Государственное образовательное учреждение высшего профессионального образования
«Санкт-Петербургский государственный электротехнический университет “ЛЭТИ” им. В.И. Ульянова (Ленина)»
(СПбГЭТУ)
ДИДАКТИЧЕСКИЕ МАТЕРИАЛЫ по дисциплине
«НАНОЭЛЕКТРОНИКА»
Для подготовки бакалавров по направлению – «Нанотехнология»
Профиль – «Нанотехнологии для систем безопасности»
Санкт – Петербург
2010
Экзаменационные вопросы по курсу "Наноэлектроника"
1.Тенденции создания нанотранзистора.
2.Основные пути развития кремниевой элементной базы.
3.Квантовое ограничение и плотность состояний в квантовых ямах, квантовых нитях и квантовых точках
4.Баллистический и квазибаллистический транспорт носителей заряда в объёмных кристаллах и структурах пониженной размерности
5.Туннелирование носителей заряда через потенциальные барьеры
6.Спиновые эффекты, туннельное магнитосопротивление и гигантское магнитосопротивление
7.Свободная поверхность и интерфейсы в наноструктурах
8.Гетероструктуры 1-го и 2-го типов (правило Андерсона)
9.Полупроводниковые сверхрешетки
10.Сверхрешётки полупроводник-диэлектрик
11.Напряжённые сверхрешётки.
12.Наноструктуры с квантовым ограничением за счет приложенного внешнего электрического поля: структуры металл-диэлектрик-полупроводник (МДПструктуры)
13.Структуры с расщепленным затвором.
14. Наноструктуры |
с |
квантовым |
ограничением |
за |
счет |
внутреннего (встроенного) электрического поля: дельта-легированные и n-i-p-i структуры
15.Модуляционно-легированные структуры
16.Квантовые ямы
17.Периодические квантовые ямы.
18.Физические явления, лежащие в основе одноэлектронного туннелирования и соответствующие наноструктуры: явление кулоновской блокады
19.Одноэлектроника
20.Однобарьерные структуры
21.Понятие о кулоновском зазоре
22.Эквивалентная схема и вольт-амперная характеристика однобарьерной структуры
23.Двухбарьерные структуры
24.Вольт-амперная характеристика двухбарьерной одноэлектронной структуры с различной прозрачностью барьеров
25.Понятие о кулоновской лестнице
129
26.Макроскопическое квантовое туннелирование (сотуннелирование)
27.Упругое и неупругое сотуннелирование.
28.Приборы на одноэлектронном туннелировании: одноэлектронный транзистор
29.Структура и эквивалентная схема одноэлектронного транзистора
30.Характеристики одноэлектронных транзисторов (кулоновские осцилляции и характеристики кулоновской блокады)
31.Одноэлектронная ловушка, профили распределения энергии в ней и её зарядовое состояние
32.Одноэлектронный турникет и генератор накачки
33.Генераторы на одноэлектронных транзисторах
34.Стандарты постоянного тока
35.Стандарты температуры
36.Управляемые напряжением логические элементы и управляемые зарядом логические элементы
37.Примеры логических элементов на одноэлектронных транзисторах
38.Одноэлектронный транзисторный параметрон
39.Основные преимущества и недостатки одноэлектронных приборов по сравнению с известными биполярными и полевыми полупроводниковыми транзисторами.
40.Резонансное туннелирование носителей заряда через потенциальные барьеры
41.Явление резонансного туннелирования
42.Энергетическая диаграмма и вольт-амперная характеристика типичной двухбарьерной структуры с квантовой ямой
43.Приборы на основе резонансного туннелирования: резонансно-туннельный диод
44.Эквивалентная схема резонансно-туннельного диода
45.Вольт-амперная и вольт-фарадная характеристики
46.Теоретические и экспериментальные данные для наиболее распространённых резонансно-туннельных диодов
47.Резонансно-туннельный биполярный транзистор и резонансно-туннельный транзистор на горячих электронах
48.Транзисторные структуры в виде управляемых затвором резонансно-туннельных диодов
49.Логические элементы на резонансно-туннельных приборах
50.Принцип работы базового резонансно-тунельного элемента, обеспечивающего переход из моностабильного в бистабильное состояние.
51.Транспорт носителей заряда вдоль потенциальных барьеров
130
52.Фазовая интерференция электронных волн: магнитный эффект Ааронова – Бома и его экспериментальное наблюдение в кольцевых тонкоплёночных структурах и углеродных нанотрубках
53.Эффект расщепления траектории движения электронов в твердом теле под действием атома примеси
54.Универсальные флуктуации проводимости.
55.Вольт-амперные характеристики низкоразмерных структур: формализм Ландауэра-Бютикера
56.Правило сложения для коэффициентов отражения и пропускания такого устройства
57.Моделирование переноса носителей заряда в реальных трехмерных системах.
58.Понятие отрицательного сопротивления изгиба: структура для измерения электрического сопротивления материала четырехзондовым методoм
59.Зависимость изменения сопротивления упомянутой структуры от напряженности магнитного поля, наложенного перпендикулярно плоскости структуры.
60.Квантовый эффект Холла (КЭХ)
61.Целочисленный квантовый эффект Холла и его сравнение с классическим эффектом
62.Дробный квантовый эффект Холла
63.Понятие об уровнях Ландау в идеальной системе, содержащей двухмерный электронный газ
64.Влияние разупорядочения энергетических зон около уровней Ландау
65.Локализованные и нелокализованные (расширенные) состояния
66.Граница подвижности
67.Фактор заполнения уровней Ландау.
68.Приборы на интерференционных эффектах: квантовый интерференционный транзистор
69.Конструкция квантового интерференционного транзистора и его численное моделирование
70.Кольцевая конструкция электронного интерференционного транзистора
71.Полевой транзистор на отраженных электронах
72.Полевой транзистор на преломлённых электронах
73.Преломляющий переключатель для баллистических электронов
74.Спин-зависимый транспорт носителей заряда:
75.Спинтроника как новое научно-техническое направление.
131
76.Гигантское магнитосопротивление: эффект гигантского магнитосопротивления в тонкопленочных структурах с протеканием тока в плоскости слоев
77.Явление осциллирующего обменного взаимодействия
78.Спин-поляризованный транспорт электронов через слоистые структуры ферромагнетик-немагнетик-ферромагнетик
79.Принцип действия спинового затвора (вентиля)
80.Псевдоспиновый затвор
81.Модель вертикального переноса носителей заряда.
82.Спин-зависимое туннелирование: эффект туннельного магнитосопротивления
83.Высокотемпературная зависимость магнитосопротивления туннельного перехода между двумя ферромагнитными тонкими пленками от направления и напряженности магнитного поля
84.Изменение магнитосопротивления туннельного перехода в зависимости от величины смещения на постоянном токе
85.Модель температурной зависимости туннельного магнитосопротивления на примере двух типичных магнитных переходов Co/Al2O3/Co/NiO и Co/Al2O3/Ni80Fe20.
86.Манипулирование спинами носителей заряда в полупроводниках: расщепление состояний носителей заряда по спинам
87.Квантовые точки в магнитном поле
88.Эффект Рашбы
89.Конкуренция спин-орбитального взаимодействие и квантового ограничения в двумерных системах
90.Механизмы переноса спин-поляризованных носителей заряда
91.Эффект Кондо: понятие о кондо-возрастании сопротивления металлов и о температуре Кондо
92.Кондо-поведение квантовых точек, управление их проводимостью.
93.Спинтронные приборы: магнитная головка воспроизведения на гигантском магнитосопротивлении
94.Энергонезависимая память на гигантском магнитосопротивлении
95.Энергонезависимая память на спин-зависимом туннелировании
96.Спин-вентильный транзистор и принцип его работы.
132
Контрольные вопросы по курсу "Наноэлектроники"
1.Что такое размерные эффекты?
2.Чем отличаются классические и квантовые размерные эффекты?
3.Каковы условия наблюдения квантовых размерных эффектов?
4.Что такое наноструктура?
5.Какие приборы можно отнести к категории наноэлектронных приборов?
6.Как выглядит энергетический спектр электрона в однородном 3D-пространстве?
7.Какие квантовые числа характеризуют стационарные состояния электрона однородном 3D-пространстве? Укажите вид его волновых функций.
8.Как изменится энергетический спектр электрона в случае ограничения его движения в одном, двух и трех направлениях?
9.Какие квантовые числа характеризуют состояния электрона в 2D-, 1D-, 0Dсистемах? Укажите примерный вид волновых функций в координатном представлении.
10.Что такое туннельный эффект?
11.Как выглядит энергетический спектр и волновые функции электрона в системе из двух туннельно-связанных квантовых ям?
12.Нарисуйте энергетический спектр системы из периодически чередующихся потенциальных ям.
13.Что такое блоховские волновые функции и как они изменяются при трансляции на произвольный вектор прямой решетки?
14.Что такое зона Бриллюэна и какие квантовые числа характеризуют состояния электрона в 1D-, 2D-, 3D-решетках?
15.Что такое резонансное туннелирование в системах с потенциальными барьерами?
16.Что такое плотность энергетических состояний и какова её размерность?
17.Изобразите плотность состояний как функцию энергии в 3D-, 2D-, 1D-, 0Dсистемах.
18.Что такое локальная плотность состояний?
19.Каков физический смысл распределения Ферми-Дирака?
20.Что такое одночастичный спектр возбуждений в многочастичной системе в приближении Хартри?
21.Изобразите возможные типы полупроводниковых гетероструктур.
22.Что такое kр-теория возмущений и эффективный kp-гамильтониан для гетероструктуры?
133
23.Как выглядит уравнение Шредингера для электрона и дырки в наногетероструктуре в приближении эффективной массы в k-представлении?
24.Как выглядит уравнение Шредингера для электрона и дырки в
наногетероструктуре в приближении эффективной массы в |
узельном |
представлении? |
|
25.Как выглядит уравнение Шредингера для электрона и дырки в наногетероструктуре в приближении эффективной массы в х-представлении?
26.Какие граничные условия накладываются на огибающую волновую функцию в х- представлении на гетерогранице?
27.Запишите выражение для локальной плотности состояний в кристалле.
28.Что такое усредненная по элементарной ячейке плотность состояний в кристалле?
29.Что такое усредненная по элементарной ячейке плотность состояний в наногетероструктуре?
30.Запишите выражение, определяющее пространственное распределение носителей заряда в наногетероструктуре.
31.Для чего необходимо самосогласованное решение уравнений Шредингера и Пуассона?
32.Как рассчитать профиль концентрации носителей заряда и распределение потенциала в наногетероструктуре, легированной донорами?
33.Как рассчитать профиль концентрации носителей заряда и распределение потенциала в наногетероструктуре, легированной акцепторами?
34.Что такое метод инвариантов?
35.Как построить эффективный гамильтониан для электронов и дырок в гетероструктуре?
36.Чем отличается kp-гамильтониан объемного полупроводника от kpгамильтониана наногетероструктуры?
37.Как определяется матричный элемент для оптических переходов в полупроводниковых гетероструктурах?
38.Напишите формулу, связывающую вероятность оптических переходов в единицу времени с матричным элементом.
39.Что такое межзонные оптические переходы?
40.Что такое внутризонные оптические переходы?
41.Что такое 2D-, 1D-, 0D-экситоны?
134
