7. Диффузионно-дрейфовая модель тока в МОПТ

7.1. Введение

Существующие простейшие модели ВАХ МОПТ основаны идеологически на формальном интегрировании выражения для омического тока, игнорируя последовательный учет диффузионного тока, что приводит к необходимости кусочного вида описания вольт-амперной характеристики отдельно для надпорогового и подпорогового участка, а также для линейного режима и режима насыщения тока транзистора (см. главу 4). Последовательное описание ВАХ с необходимостью требует решения уравнения непрерывности для тока в канале. Действительно, уравнение непрерывности для тока является неотъемлемой частью т.н. фундаментальной системы уравнений, включающей в себя также уравнение Пуассона, граничные условия и уравнения переноса носителей тока. Например, теория биполярного транзистора изначально базируется на решении уравнений непрерывности для тока неосновных носителей в базе. В этой главе описан подход, основанный на явном аналитическом решении для уравнения непрерывности тока в канале, что позволяет получить в компактном виде замкнутые выражения для тока, а также для распределения электрических полей, потенциалов и плотности носителей в канале при любом напряжении на затворе. Для этого необходимо более детально рассмотреть задачу о распределении электрохимического потенциала в канале транзистора.

7.2. Электрохимический потенциал в канале МОПТ

Хорошо известно, что разность напряжений между контактами представляется разностью электрохимических потенциалов. Электрохимический потенциал является суммой электрического и химического потенциалов и его распределение отслеживает распределение локального уровня Ферми. В частности, распределение электрохимического потенциала вдоль канала можно записать в

виде (здесь используется обозначение ζ (y)= ζ (y) > 0 )

169

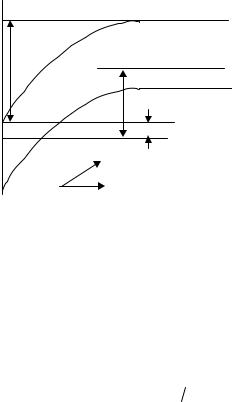
При VDS = 0 электрохимический потенциал в кремнии постоянен μ(x, y) = const. При ненулевом смещении между стоком и истоком VDS > 0 , изменение электрохимического потенциала вдоль

канала, как уже обсуждалось в главе 4, есть локальное значение обратного смещения между каналом и подложкой (рис. 7.1)

μ(y)q =VCB (y) = ϕS (y)+ζ (y).

Отметим, что в физической литературе под химическим потенциалом чаще всего подразумевают величину со знаком, противоположным знаку в выражении (7.2.1). В этом случае химический потенциал оказывается положительной величиной для вырожденных систем и отрицательной для невырожденных.

Рис. 7.1. Зонная диаграмма n-МОПТ, показывающая локальное значение электрохимического потенциала в точке y по длине канала

В этой главе мы будем рассматривать канал МОПТ в приближении невырожденного электронного газа, при котором удобнее пользоваться соглашением о знаке химического потенциала, определенного как в (7.2.1). Кроме того, следует иметь в виду, что в литературе очень часто электрохимический потенциал μ (стандарт-

ное обозначение) называют просто химическим потенциалом. Изменение поверхностного электрического потенциала характе-

ризуется изменением положения краев зон

170

а изменение химического потенциала вдоль канала характеризуется изменением объемной концентрации электронов вдоль канала

n = NC exp(−(EC (x)− EFn )kT )≡ NC exp(−ζ (y)kT ). (7.2.3)

Приложенное внешнее напряжение между стоком и истоком приводит, в общем случае, как к изменению электрического потенциала (электрических полей), так и к изменению химического потенциала (т.е. к пространственному перераспределению плотности носителей), но с выполнением условия

Хорошо известно, что величина тока определяется градиентом электрохимического потенциала μ . Поэтому в отсутствие тока оба

слагаемых не являются независимыми величинами и их пространственные изменения в точности компенсируют друг друга, как это имеет место в равновесном pn-переходе. В неравновесных условиях пространственные изменения химического и электрического потенциала в МОП транзисторах связаны между собой только условием электронейтральности и могут управляться за счет изменения напряжения на внешних электродах.

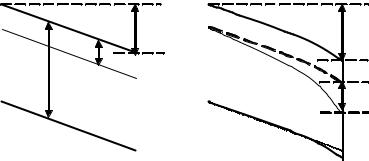
Отметим принципиальную разницу в распределении электрохимического потенциала в однородном проводнике и канале МОП транзистора, а также в большинстве других наноэлектронных структур. В однородном полупроводнике (либо в металле) концентрация носителей вдоль длины образца и, соответственно, химический потенциал остаются постоянными, поскольку приложенное напряжение никак не влияет на объемную локальную электронейтральность (рис. 7.2, а).

В приборных структурах электронейтральность обеспечивается за счет перераспределения поверхностной плотности заряда разного знака в планарных слоях. Поэтому, как мы уже отмечали выше, в канале n-МОПТ плотность электронов уменьшается по мере приближения к стоку и химический потенциал изменяется (рис. 7.2, б).

171