
- •Министерство образования и науки российской федерации
- •2011 Г.
- •Требования к оформлению контрольных работ
- •Формирование исходных данных к задачам
- •Линейная алгебра
- •Интегральное исчисление.
- •Функции нескольких переменных.
- •Двойные, тройные и криволинейные интегралы.
- •Элементы теории поля.
- •Дифференциальные уравнения.
- •Функции комплексного переменного.
- •Операционное исчисление.
- •Теория вероятностей.
- •Элементы математической статистики
- •Линейное программирование.
- •Математические методы в экономике.
- •Дискретная математика.
- •Краткое содержание (программа) курса
- •1. Линейная алгебра.
- •2. Аналитичеcкая геометрия.
- •3. Дифференциальное исчисление.
- •4. Интегральное исчисление.
- •5. Функции нескольких переменных.
- •6. Двойные, тройные и криволинейные интегралы.
- •7. Элементы теории поля.
- •8. Обыкновенные дифференциальные уравнения и их системы.
- •9. Ряды.
- •10. Функции комплексного переменного.
- •11. Операционное исчисление.
- •12. Теория вероятностей.
- •13. Математическая статистика.
- •14. Линейное программирование.
- •15. Математические методы в экономике.
- •16. Дискретная математика.
- •Список учебной литературы
Интегральное исчисление.
Неопределенный интеграл.
Найти интегралы:
а)
 ; б)
; б) ;
д)
;
д) .
.
Несобственные интегралы.
Вычислить интеграл или установить его расходимость:

Применения определенных интегралов.
Построить схематический чертеж и найти площадь фигуры, ограниченной линиями:
 ;
;
Найти объем тела, полученного при вращении вокруг оси ОХ фигуры, ограниченной линиями:
 .
.
Функции нескольких переменных.
Частные производные и дифференциал функции.
Найти частные производные
 ,
, ,
, функции
функции
 .
.Показать, что функция
 удовлетворяет уравнению
удовлетворяет уравнению .
.
Приложения частных производных.
Для функции
 в точке
в точке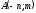 найти градиент и производную по
направлению
найти градиент и производную по
направлению .
.Найти наибольшее и наименьшее значения функции
z = 4x2 + y2 – 4mx – 2ny + m2 + n2 в области заданной неравенствами:
x
≥ 0; nx – my 0; x+ y – m – n
0; x+ y – m – n 0
0
Двойные, тройные и криволинейные интегралы.
Двойные интегралы.
Изменить порядок интегрирования:
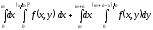 .
.
Сделать чертеж и найти объем тела, ограниченного поверхностями
 и плоскостью, проходящей через точки
и плоскостью, проходящей через точки и
и .
.Сделать чертеж и найти площадь фигуры, ограниченной линиями:
а)
 .
.
Тройные интегралы.
Найти
 ,
если телоV
ограниченно плоскостями
,
если телоV
ограниченно плоскостями
 и
и .
.Найти объем тела, ограниченного поверхностями
 .
.
Криволинейные интегралы.
Вычислить
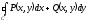 ,
где
,
где ,
, ,
а контурС
образован линиями
,
а контурС
образован линиями
 ,
, :
а) непосредственно; б) по формуле
Грина.
:
а) непосредственно; б) по формуле
Грина.Вычислить
 ,
где контурС
является одним витком винтовой линии:
,
где контурС
является одним витком винтовой линии:
 .
.
Элементы теории поля.
Дифференциальные операции.
В точке
 составить уравнение касательной
прямой и нормальной плоскости к кривой
составить уравнение касательной
прямой и нормальной плоскости к кривой
 .
.
Найти в точке
 градиент скалярного поля
градиент скалярного поля
 .
.
Найти в точке
 дивергенцию векторного поля
дивергенцию векторного поля
 .
.
Найти в точке
 ротор векторного поля
ротор векторного поля
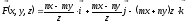 .
.
Интегралы и интегральные теоремы.
Убедиться, что поле
 потенциально, и найти его потенциал.
потенциально, и найти его потенциал.Даны поле
 и цилиндрD,
ограниченный поверхностями z=0,
z=m,
x2+y2=(n+1)2.
Найти:
и цилиндрD,
ограниченный поверхностями z=0,
z=m,
x2+y2=(n+1)2.
Найти:
а)
поток поля
 через боковую поверхность цилиндра в
направлении внешней нормали;
через боковую поверхность цилиндра в
направлении внешней нормали;
б)
поток поля
 через всю поверхность цилиндра в
направлении внешней нормали непосредственно
и с помощью теоремы Остроградского –
Гаусса.
через всю поверхность цилиндра в
направлении внешней нормали непосредственно
и с помощью теоремы Остроградского –
Гаусса.
Даны поле
 и замкнутый виток
и замкнутый виток ,
, ( обход контура происходит в направлении,
соответствующем возрастанию параметра
φ). Найти циркуляцию поля
( обход контура происходит в направлении,
соответствующем возрастанию параметра
φ). Найти циркуляцию поля вдоль контураγ
непосредственно и с помощью теоремы
Стокса.
вдоль контураγ
непосредственно и с помощью теоремы
Стокса.
Дифференциальные уравнения.
Уравнения первого порядка.
Найти общее решение уравнения:
а)
 ;
в)
;
в)
 .
.
Скорость роста банковского вклада пропорциональна с коэффициентом равным
 величине вклада. Найти закон изменения
величины вклада со временем, если
первоначальная сумма вклада составляла
величине вклада. Найти закон изменения
величины вклада со временем, если
первоначальная сумма вклада составляла миллионов рублей.
миллионов рублей.Линейные уравнения высших порядков.
Решить задачу Коши:
а)
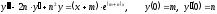
б)

Системы линейных уравнений.
Решить систему линейных уравнений
 с начальными условиями
с начальными условиями .
.
Ряды.
Числовые ряды.
Исследовать на сходимость ряды с положительными членами:
а)
 ; б)
; б)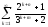 ;
;
в)
 ; г)
; г) .
.
Исследовать на условную сходимость и абсолютную сходимость знакочередующиеся ряды:
а)
 ; б)
; б) .
.
Степенные ряды.
Найти область сходимости степенного ряда:
а)
 ;
б)
;
б) .
.
Разложить функцию
 в ряд Тейлора в окрестности точки х0:
в ряд Тейлора в окрестности точки х0:
а)
 ; б)
; б)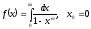 .
.
С помощью разложения в ряд вычислить приближенно с точностью 0,001 значения:
а)
 ; б)
; б) .
.
Ряды Фурье.
Разложить функцию
 в ряд Фурье в указанном интервале:
в ряд Фурье в указанном интервале:
а)

в интервале
 ;
;
б)
 в интервале
в интервале .
.
в)
 в интервале
в интервале .
.
