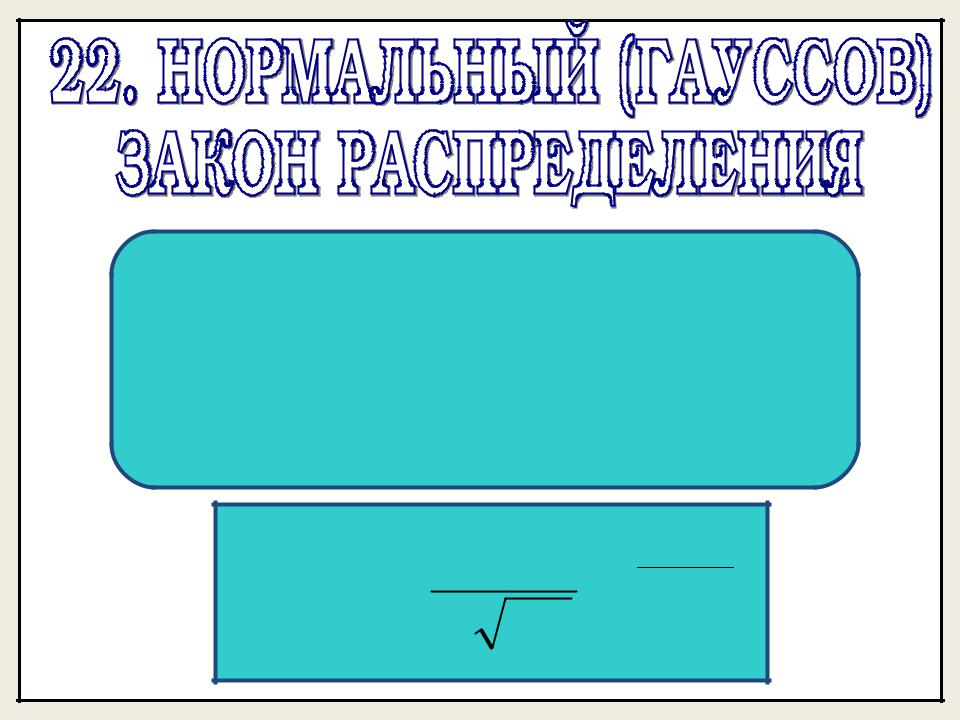
Непрерывная случайная величина Х |
|||
называется распределенной |
|||
по нормальному закону с параметрами |
|||
a, σ>0, если она имеет плотность |
|||
вероятности |
|
||
f (x) |
1 |
|
( x a)2 |
2 |
e |
2 2 |
|
|
|
||
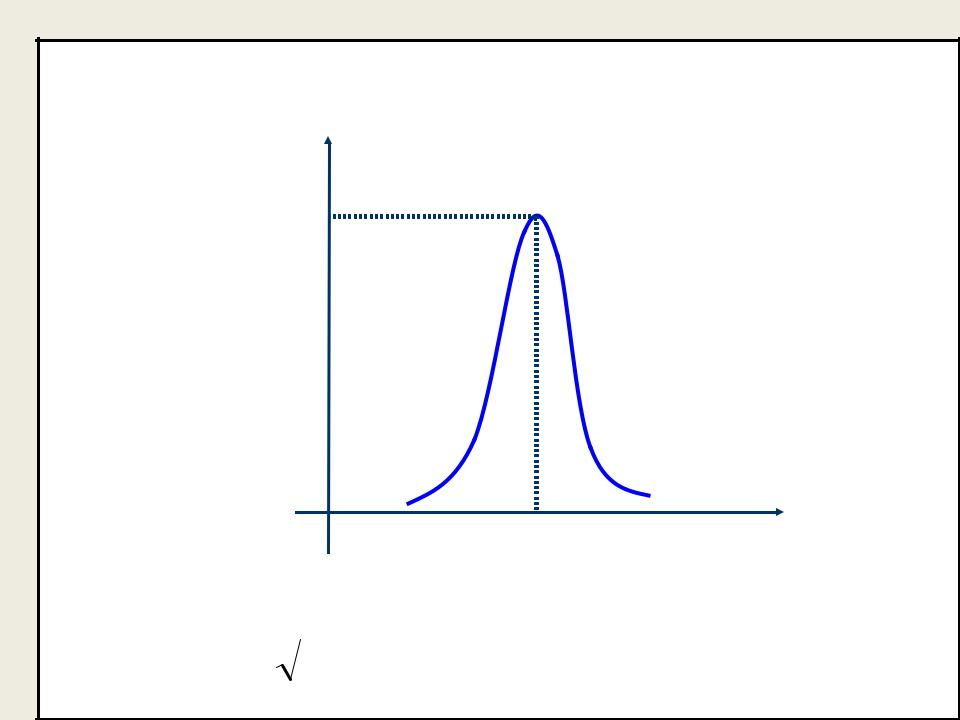
Кривая распределения имеет вид:
f (x) t
a
x
Где |
t |
|
1 |
|
|
|
|
|
|
||
|
2 |
|
|||
|
|
|
|
||
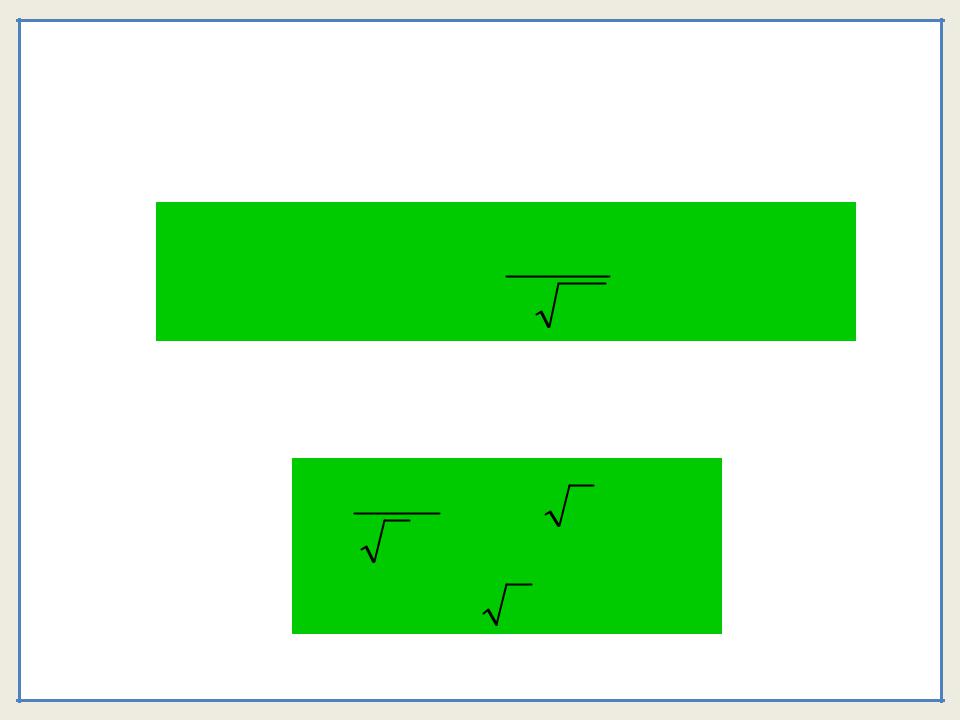
Выясним смысл параметров распределения Гаусса. |
|||||||
Для этого вычислим характеристики этого |
|||||||
распределения |
(математическое |
ожидание |
и |
||||
дисперсию). |
|
|
|
|
|
( x a)2 |
|
|
|
|
1 |
|
|
|
|
M[X ] x f (x)dx |
x e |
2 2 dx |
|
||||
|
|
|
2 |
|
|
|
|
Делаем замену переменной: |
|
|
|
|
|
||
t x a |
x 2 t a |
|
|||||
|
2 |
|
|
|
|
|
|
|
dx |
2 dt |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
t a) e t 2 |
|
|
|||||||||||
|
|
|
|
|
|
|
( |
2 |
2 |
dt |
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
( |
|
t a) e t 2 dt |
|||||||||||||||
|
|
|
|
|
|
2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Разбиваем на сумму двух интегралов: |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
2 |
a |
||||||||||||||||||
|
|
|
t e t 2 dt |
|
e t 2 dt |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Второй интеграл представляет собой интеграл Пуассона:
e t 2 dt 
В первом интеграле вносим t под знак дифференциала:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
a |
e t2 |
|
||||||||||||||
|
e t2 d(t2 ) |
a a |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
|
|||||||||||||
|
|
|
|
|
|
||||||||||||
Таким образом, параметр a представляет собой математическое ожидание случайной величины.
Теперь найдем дисперсию:
|
|
|
1 |
|
|
e |
( x a)2 |
|
D[X ] (x mx )2 |
f (x)dx |
|
|
(x a)2 |
2 2 |
|||
|
|
|
|
|||||
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||
dx
Делаем замену переменной:
|
|
|
|
|
|
|
t |
x |
|
a |
|
x a |
|
t |
|
|||||
|
|
|
|
2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
dx |
|
|
dt |
|
|||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||
|
|
1 |
|
|
|
|
|
|
dt 2 2 |
|
|
|||||||||
|
|
|
( |
|
t)2 e t 2 |
|
|
t 2 e t 2 dt |
||||||||||||
|
|
|
2 |
2 |
||||||||||||||||
|
|
|
|
|||||||||||||||||
|
|
|||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||
Этот интеграл берем по частям:
|
|
|
|
|
t u; |
2t e t2 dt dv |
|
|
|||||
|
|
|
|
|
dt du; |
v e t 2 |
|
|
|||||
|
2 |
|
t 2 |
|
|
|
|
t 2 |
|
|
|||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
( e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
t e |
|
|
|
|
|
)dt |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
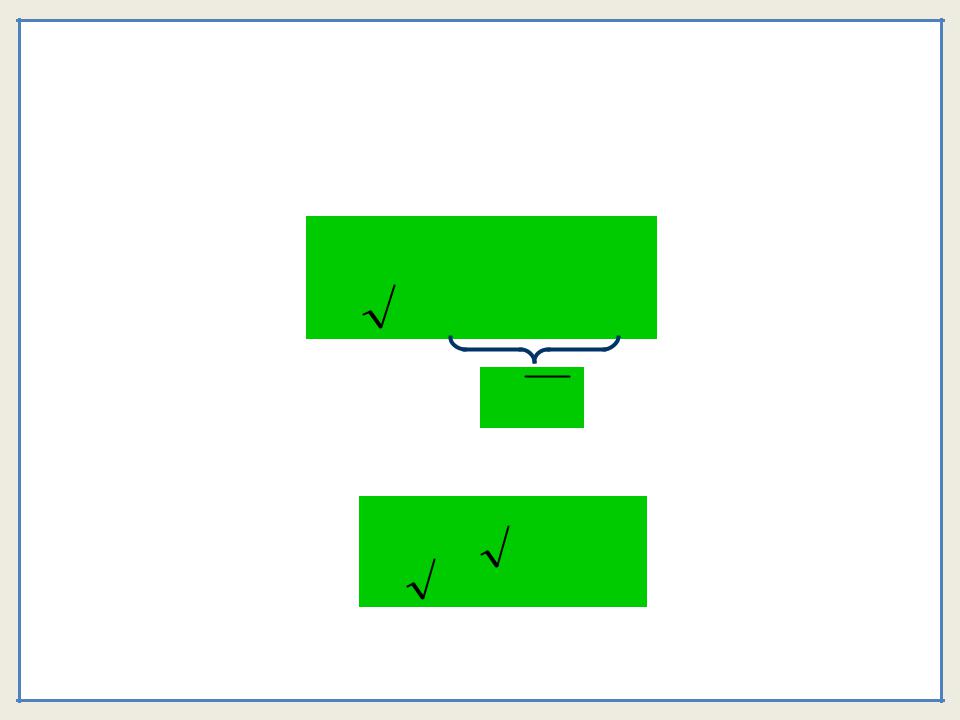
Первое слагаемое в скобках равно 0, так как экспонента в минус бесконечной степени будет стремиться к нулю быстрее, чем возрастает любая степень t.
|
|
2 |
|
|
|
|
|
|
2 |
|
|||
|
|
|
|
|
e t |
dt |
|
|
|
|
|||
|
|
|
||||
|
|
|
|
|||
Этот интеграл представляет собой интеграл
Пуассона: |
2 |
|
|
||||
|
|
|
|||||
|
2 |
||||||
|
|
|
|
||||
|
σ |
||||||
Тогда параметр |
|
представляет собой |
|||||
среднеквадратичное отклонение.
Если изменять параметр a , кривая распределения будет смещаться вдоль оси абсцисс, не изменяя при этом своей формы.
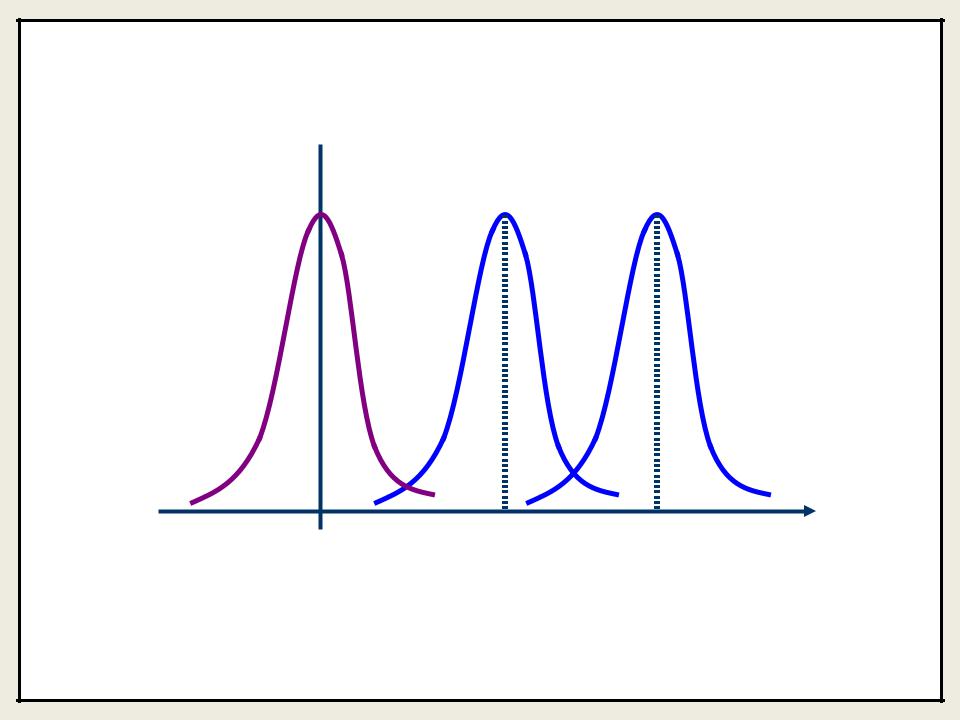
f (x) 
a 0 |
a1 |
a2 |
x |
Параметр σ характеризует не положение, а саму форму кривой распределения. При его увеличении кривая
распределения становится более плоской, и наоборот.
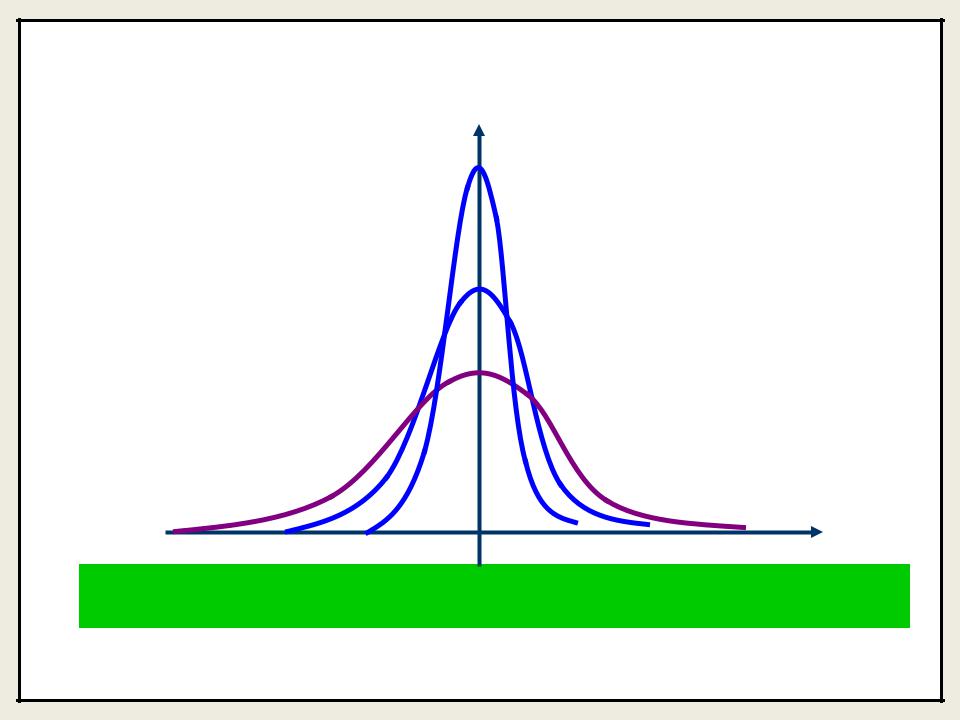
f (x)
1
2
|
3 |
σ1< σ2< σ3 |
x |
То, что случайная величина Х распределена по нормальному закону с параметрами a, σ>0 , обозначается
X N(a, )
При вычислении вероятностей такая случайная величина сводится к случайной величине
Z N (0,1)