Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Международный университет МИТСО

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Ан.геом. в пространстве

.pdf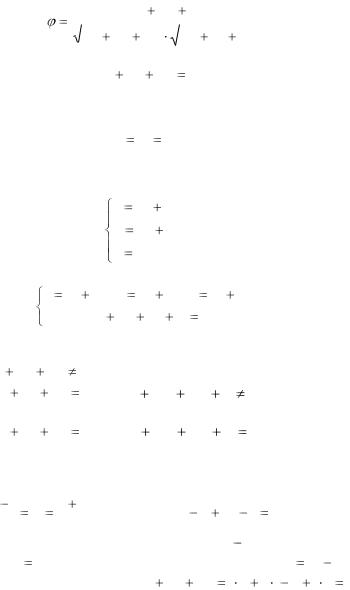

Скачиваний:

Добавлен:

15.02.2016

Размер:

783.91 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 33

sin		Am Bn	Cp	.


	A2 B2 C 2		m2 n2 p2
	A2 B2 C 2		m2 n2 p2

Условие параллельности прямой и плоскости:

Am Bn Cp 0 .

Условие перпендикулярности прямой и плоскости:

A	B	C	.
			.
m	n	p

2. Для нахождения точки пересечения прямой и плоскости удобно воспользоваться параметрическими уравнениями прямой

x x0 mt , y y0 nt, z z0 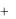pt;

координаты точки пересечения находятся из системы уравнений:

x x0 mt, y y0	nt, z z0 pt,
Ax By Cz	D 0.

3. В пространстве возможны три случая взаимного расположения

прямой и плоскости:

1) если Am

Cp 0 , то прямая пересекает плоскость;

2) если Am

Ax0

By0 Cz0

0 , то прямая па-

раллельна плоскости;

3) если Am

Ax0

By0

Cz0

0 , то прямая ле-

жит в плоскости.

Пример 4.1. Установить взаимное расположение прямой

и плоскости 2x

0 .

Решение. Прямая проходит через точку M0 (1;0; 1) ,

направляющий

вектор прямой s

(1;4;1). Нормальный вектор плоскости n

(2; 1;2).

Найдем значение

выражения

Am Bn

1 2

4 ( 1)

1 2 0.

Следовательно, данная прямая параллельна плоскости или лежит на ней.

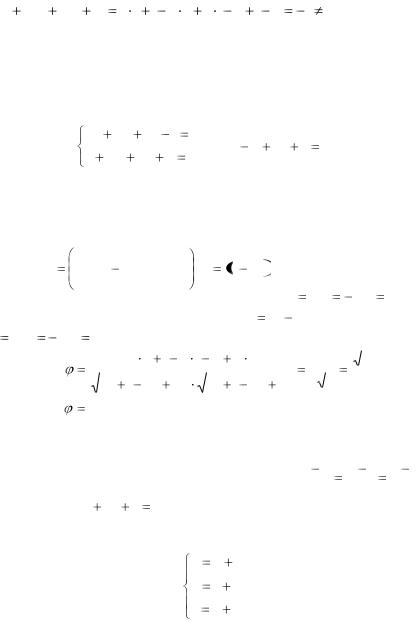
Проверим	условие	принадлежности	прямой	плоскости:
Ax0 By0 Cz0	D 2 1	( 1) 0 2 ( 1) ( 4)	4 0.	Условие не

выполняется, поэтому прямая не принадлежит плоскости. Таким образом, данные прямая и плоскость параллельны и не имеют общих точек.

Ответ: прямая и плоскость параллельны.

Пример 4.2. Найти угол между прямой и плоскостью, заданных

уравнениями:	2x	3y	3z	1	0,	и	2x y 2z 4 0.
	x	2 y	2z	5	0

Решение. В данном случае прямая задана общими уравнениями, как линия пересечения двух плоскостей. Направляющий вектор этой прямой найдем по формуле (6).

Итак,

s		3	3	;	2		3	;	2	3	, s	0; 1;1 .
		2	2		1		2		1	2				Таким образом,
													m		0, n					1, p	1.
Нормальный вектор заданной плоскости n													(2; 1;2),				т. е.
A 2, B	1,C		2.
							0		(	1)	( 1)	2 1
Тогда sin						2	0		(	1)	( 1)	2 1				3		2			и, сле-

																		2
			22		( 1)2					22	02	( 1)2	12	3 2
			22		( 1)2					22	02	( 1)2	12	3 2
довательно,			45 .
Ответ: 45 .
Пример 4.3. Найти точку пересечения прямой														x		2			y 1			z 3
Пример 4.3. Найти точку пересечения прямой														2					3			1
														2					3			1
с плоскостью 2x 3y						z	0.

Решение. Параметрические уравнения прямой имеют вид: x 2 2t,

y 1 3t, z 3 t.

Для определения точки пересечения прямой и плоскости подставим выражения для x, y, z из уравнений прямой в уравнение плоско-

сти. Получим 2 (2 2t) 3 (1 3t) 3 t 0, откуда находим t								5	.
сти. Получим 2 (2 2t) 3 (1 3t) 3 t 0, откуда находим t								7	.
								7
Следовательно, координатами точки пересечения будут x						4	,
Следовательно, координатами точки пересечения будут x						7	,
						7
y	8	, z		16	.
y	7	, z	7		.
	7		7

Итак, прямая и плоскость пересекаются в точке M 74 ; 87 ;167 .

Ответ: M 74 ; 87 ;167 .

Пример

4.4.

При

каких

значениях

прямая

y 2

лежит в плоскости 4x

0 ?

Решение.

Подставляя

уравнения

Ax0

By0

Cz0

0 соответствующие значения, получим систему

уравнений

B (

(

из

которой

определяем

4 1

B (

(

2 и D

Ответ: B 2 , D 8.

Пример 4.5. Определить уравнение плоскости Q ,

проходящей че-

рез точку

M (1;2;3)

параллельно прямым

(L )

(L ) .

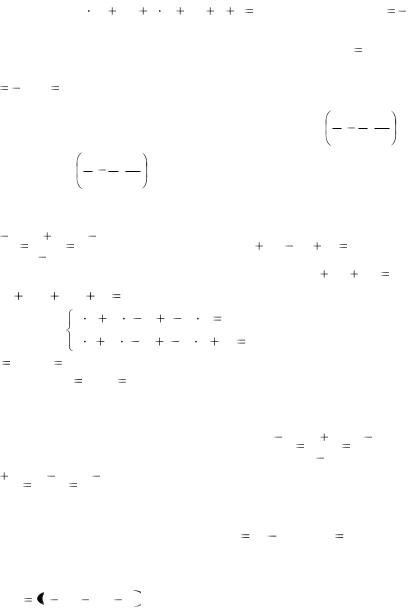
Решение.

Так как плоскость Q параллельна прямым

и L2 , то

направляющие векторы этих прямых s1

(4;

1;3) и s2

(2;4;5)

парал-

лельны плоскости Q .

Пусть M (x; y; z)

− произвольная точка плоскости Q . Тогда вектор

M1M

1; y

2; z

лежит в плоскости Q .

Условие (необходимое и достаточное) компланарности векторов

		x1	y1	z1
a1 x1; y1; z1 , a2	x2; y2 ; z2 , a3 x3; y3; z3 :	x2	y2	z2	0 .
		x3	y3	z3


Условие компланарности векторов M1M , s1											и s2 позволяет полу-
чить уравнение плоскости Q :
					x 1	y	2		z	3
					x 1	y	2		z	3
					4		1			3
					2		4			5
5 (x	1)	6 ( y	2)	16 (z	3)	2	(z	3)		12 (x	1)	20	( y 2)
17 x	14 y	18z	9	0.
Отсюда уравнение плоскости Q имеет вид: 17 x												14 y	18 z 9 0.
Ответ: 17 x			14 y	18 z	9	0.
Пример 4.6. Определить проекцию точки M (1;2;3)													на плоскость
2x 3y 4z 5 0.
Решение.		Проведем через точку						M прямую,				перпендикулярную

плоскости. Точка пересечения этой прямой и плоскости будет проекцией точки M на плоскость.

За направляющий вектор прямой s возьмем нормаль плоскости: s n 2;3; 4 .

x 1 2t,

Тогда параметрические уравнения прямой y 2 3t, z 3 4t.

Найдем точку пересечения прямой и плоскости. Выполним следующие действия:

2x 3y 4z 5 0,

2 (1 2t) 3(2 3t) 4 (3 4t) 5 0, 29t 9 0.

Отсюда t 299 .

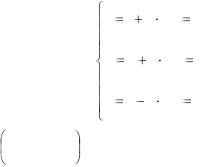
Подставив это значение параметра в уравнения прямой, получим координаты проекции точки M на плоскость:

						x	1	2	9		47			,
						x	1	2	29		29			,
									29		29
						y	2	3		9			85		,
						y	2	3	29		29				,
									29		29
						z	3	4	9			51		.
						z	3	4						.
									29		29
Ответ:	47	;	85	;	51	.
Ответ:	29	;	29	;	29	.
	29		29		29

ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ

Студент выполняет индивидуальные задания по варианту, номер которого соответствует номеру его фамилии в журнале посещаемости занятий. Работа должна быть выполнена в отдельной тетради. Условие каждого задания следует записывать полностью, а решения подробно. Студент защищает свою работу у преподавателя.

Задание 1. Определить уравнение плоскости Q , зная точку

M 0 (h; k; m) в этой плоскости и нормаль n (q; p;m) плоскости. Определить, принадлежат ли точки M1( 1;3;2) и M2 (9; 2;1) плоскости Q. Составить уравнение плоскости Q в отрезках. Привести уравнение плоскости Q к нормальному виду. Определить расстояние от точки P( n; q; p) до плоскости Q . Определить уравнение плоскости Q1 , проходящей через точку C(q; p;m) параллельно плоскости Q.

Задание 2. Известны точка A(h;k;q) на прямой и направляющий вектор s (m;n; p) этой прямой. Определить канонические и параметрические уравнения прямой. Определить канонические уравнения прямой, проходящей через точки A(h;k;q) и B(m;n; p) .

Задание 3. Определить канонические и параметрические уравнения hx ky mz 7 0,

прямой	nx qy	pz 9 0.	Определить взаимное расположение

этой прямой и плоскости из задания 1.

Задание 4. Определить синус угла между построенной прямой из

задания 2 и плоскостью Q из задания 1.

Вариант	h	k	m	n	q	p
1	9	2	6	8	2	1
2	2	1	3	6	8	7
3	6	7	1	4	4	6
4	9	3	7	3	8	3

Вариант	h	k	m	n	q	p
5	7	3	5	3	5	4
6	3	2	9	3	6	9
7	6	4	3	8	2	2
8	9	7	3	2	5	3
9	3	7	5	4	2	4
10	8	4	2	6	8	9
11	9	1	2	5	2	9
12	1	2	8	7	9	7
13	6	5	7	4	7	1
14	3	6	1	8	5	4
15	8	5	2	6	9	7
16	6	3	5	7	3	2
17	7	3	9	6	4	5
18	8	5	5	1	1	3
19	6	7	6	6	2	4
20	3	3	9	3	8	9
21	9	6	9	4	8	7
22	7	1	8	8	7	2
23	1	5	6	2	2	1
24	8	7	2	3	7	8
25	9	4	7	5	8	4
26	3	6	1	6	4	7
27	6	1	2	4	1	8
28	4	5	4	1	9	2
29	1	3	7	5	6	5
30	7	6	9	1	4	1
31	6	2	3	2	6	7
32	3	2	4	2	5	5
33	9	6	5	3	4	2
34	8	7	4	4	1	6
35	3	4	9	3	6	3
36	5	1	2	4	6	8
37	1	2	5	3	1	4
38	7	6	1	6	9	1
39	9	1	4	8	2	6
40	6	3	9	6	7	5

<<< < Предыдущая 1 23 / 33

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.02.201658.7 Кб9VED_zs_Shevchenko.docx
#
15.02.2016196.1 Кб25Voprosy_k_ekzamenu_ekonomika_organizatsii.doc
#
19.07.2019311.81 Кб5Zadaniye_SURS_AHD.doc
#
15.02.2016162.3 Кб11ZFO_Logistika_5k9sem-1.doc
#
15.02.201648.47 Кб45Адноклубова.docx
#
15.02.2016783.91 Кб15Ан.геом. в пространстве.pdf
#
15.02.2016112.64 Кб19Анализ деятельности предприятия.doc
#
15.02.201643.53 Кб12Архипова.docx
#
15.02.2016411.65 Кб41бел мова шпора.doc
#
15.02.2016617.05 Кб52Белорусский орнамент сакральное значение.docx
#
15.02.2016540.16 Кб51Билеты гаи.doc