
Ан.геом. в пространстве
.pdf
9. Плоскость P , проходящая через точку M1(x1; y1; z1) и перпендикулярная к двум (непараллельным) плоскостям Q1 , Q2 :
A1x B1 y C1z D1 0 , A2 x B2 y C2 z D2 0 ,
представляется уравнением
x x1 y y1 z z1
A1 |
B1 |
C1 0 . |
(5) |
A2 B2 C2
Замечание. В случае параллельности плоскостей Q1 , Q2 плоскость
P неопределенна. В соответствии с этим уравнение обращается в тождество.
Пример 2.1. Составить уравнение плоскости, проходящей через точку M (1; 2;3) и перпендикулярной вектору n (3; 4;5) .
Решение. Подставив координаты точки и координаты нормального вектора в уравнение плоскости (3), получим:
3 (x 1) 4
(x 1) 4  ( y 2) 5
( y 2) 5  (z 3) 0 , 3x 4 y 5z 26 0 . Ответ: 3x 4 y 5z 26 0 .
(z 3) 0 , 3x 4 y 5z 26 0 . Ответ: 3x 4 y 5z 26 0 .
Пример |
2.2. Что можно сказать о расположении плоскости |
x 3y 5 |
0 ? |
Решение. Так как в уравнении плоскости нет переменной z , а коэффициент D 5 0, то плоскость параллельна координатной оси
Oz.
Ответ: плоскость параллельна координатной оси Oz.
Пример 2.3. Из уравнения плоскости 3x 4 y 5z 9 0 получить
уравнение плоскости в отрезках.
Решение. Выполним следующую цепочку преобразований:
|
|
|
3x 4 y 5z 9 0 , 3x 4 y 5z |
|
9 , |
||||||||||||||||||||||
|
|
|
|
|
|
3x 4 y 5z |
1, |
|
|
x 4 y 5z |
1 |
, |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
9 |
|
|
3 |
9 |
9 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
y |
|
|
z |
1. |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
3 |
|
9 |
|
|
9 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
4 |
|
5 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Ответ: |
x |
y |
|
|
|
z |
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3 |
|
9 |
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
4 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
11

Пример 2.4. Составить уравнение плоскости, проходящей через точку M (3; 2;7) параллельно плоскости 2x 3z 5 0 .
Решение. Так как искомая плоскость и данная параллельны, то у них общий нормальный вектор. Таким образом, получим: через данную точку M (3; 2;7) провести плоскость, перпендикулярную данно-
му вектору n (2;0; 3) . Уравнение плоскости имеет вид (3). Подставив координаты точки и координаты нормального вектора,
получим: 2 (x |
3) |
3 (z |
7) 0 , 2x 3z 27 0 . |
Ответ: 2x |
3z |
27 |
0 . |
Пример 2.5. Уравнение плоскости 2x 6 y 3z 14 0 привести к
нормальному виду.
Решение. Умножим обе части уравнения на нормирующий множитель (перед корнем будет знак «плюс», т. к. D 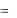 14 ):
14 ):
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
( |
6) |
2 |
2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|||||||
Получим |
|
1 |
|
(2x |
6 y |
3z |
14) |
|
1 |
|
0 , |
|
2 |
x |
|
|
6 |
y |
3 |
z 2 0 . |
|||||||||
7 |
|
|
7 |
|
|
7 |
7 |
7 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Ответ: |
2 |
x |
|
6 |
y |
|
3 |
z |
2 |
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
7 |
|
|
7 |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 2.6. Составить уравнение плоскости, проходящей через точку M (1; 2;3) и точку M1(0;2;5) , и параллельной оси Oy .
Решение. Так как плоскость параллельна оси Oy , то в уравнении
Ax By Cz D 0
ее коэффициент B |
|
0 , т. е. уравнение плоскости имеет вид: |
|
|
||||||
|
|
|
|
|
|
Ax Cz D 0 . |
|
|
|
|
Так как точки M (1; |
2;3) и M1(0;2;5) лежат на плоскости, то их коор- |
|||||||||
динаты должны удовлетворять ее уравнению, т. е. |
A 3C |
D |
0, от- |
|||||||
|
|
|
|
|
|
|
5C |
D |
0, |
|
куда A |
2 |
D ; |
C |
|
1 |
D ; следовательно, уравнение |
плоскости |
|||
5 |
5 |
|||||||||
|
|
|
|
|
|
|
||||
12

|
2 |
x |
1 |
z |
1 |
D |
0 , |
или (после сокращения на D 0 ) |
|
5 |
5 |
||||||||
|
|
|
|
|
|
||||
2x z 5 0 . |
|
|
|
||||||
Ответ: |
2x |
z |
5 |
0 . |
|||||
Пример 2.7. Составить уравнение плоскости, проходящей через две
точки |
M1(1;2;3) и M2 (2;1;1) перпендикулярно к плоскости |
3x 4 y |
z 6 0 . |
Решение. Подставив координаты точек и нормального вектора в уравнение плоскости (4), получим:
x |
1 |
y |
|
2 z 3 |
|
x 1 y 2 z 3 |
|
||
2 |
1 |
1 |
|
2 1 3 |
0 , |
1 |
1 |
2 |
0 , |
|
3 |
|
4 |
1 |
|
3 |
4 |
1 |
|
|
|
|
|
|
|
|
|
|
|
(x 1) 6  ( y 2) 4
( y 2) 4  (z 3) 3
(z 3) 3 (z 3) 8
(z 3) 8  (x 1) ( y 2) 0 , 7x 7 y 7z 14 0 , x y z 2 0 .
(x 1) ( y 2) 0 , 7x 7 y 7z 14 0 , x y z 2 0 .
Ответ: x y z 2 0 .
Пример 2.8. Составить уравнение плоскости, проходящей через точку (1;3;2) перпендикулярно к плоскостям x 2 y z 4 0 ,
2x y 3z 5 0 .
Решение. Подставив координаты точки и нормальных векторов в уравнение плоскости (5), получим:
x 1 |
y 3 |
z |
2 |
|
1 |
2 |
1 |
|
0 , |
2 |
1 |
3 |
|
|
|
|
|
|
|
6  (x 1) 2
(x 1) 2  ( y 3) z 2 4
( y 3) z 2 4  (z 2) x 1 3
(z 2) x 1 3 ( y 3) 0 , 5x y 3z 4 0 .
( y 3) 0 , 5x y 3z 4 0 .
Ответ: 5x y 3z 4 0 .
13
3.Прямая в пространстве
1.Канонические уравнения прямой, проходящей через данную точ-
ку M0 (x0; y0; z0 ) параллельно вектору s |
(m; n; p) : |
|||||
|
x x0 |
|
y y0 |
|
z z0 |
. |
|
|
|
|
|
|
|
|
m |
|
n |
p |
||
Всякий ненулевой вектор, параллельный данной прямой, называет-
ся направляющим вектором этой прямой.
Вектор s (m; n; p) − направляющий для прямой.
2. Прямую в пространстве можно задать как линию пересечения двух непараллельных плоскостей.
Общие уравнения прямой:
A1x B1 y C1z D1 0, A2 x B2 y C2 z D2 0
(коэффициенты при переменных не пропорциональны).
Направляющий вектор данной прямой находится по формуле:
s |
B1 |
C1 |
; |
|
A1 |
C1 |
; |
A1 |
B1 |
. |
(6) |
|
B2 |
C2 |
|
|
A2 |
C2 |
|
A2 |
B2 |
|
|
|
|
|
|
|
|
|
|
x |
x0 |
mt , |
|
3. Параметрические уравнения прямой: |
y |
y0 |
nt, |
|
|||||||
|
|
|
|
|
|
|
|
z |
z0 |
pt, |
|
где t − переменный параметр, t |
R . |
|
|
|
|
|
|
||||
4. Уравнения прямой, проходящей через две точки M1(x1; y1; z1) и
M2 (x2 ; y2 ; z2 ) , где x1 x2 , |
y1 |
|
y2 , z1 |
z2 , имеют вид: |
|||||
|
x |
x1 |
|
y |
y1 |
|
z |
z1 |
. |
|
|
|
|
|
|
|
|
|
|
|
x2 |
x1 |
|
y2 |
y1 |
|
z2 |
z1 |
|
5. Угол 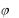 между двумя прямыми, заданными их каноническими уравнениями
между двумя прямыми, заданными их каноническими уравнениями
x x1 |
|
y y1 |
|
z z1 |
s1 |
(m1;n1; p1) , |
m1 |
|
n1 |
|
p1 |
||
|
|
|
|
14
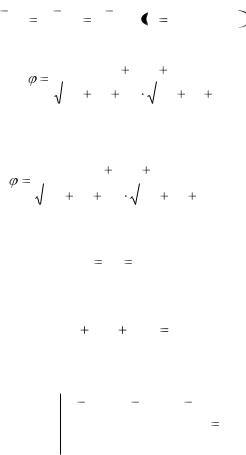
|
x x2 y |
|
y2 |
|
z z2 |
|
s2 |
(m2;n2; p2 ) |
|
||||||||
|
m2 |
|
|
n2 |
|
|
p2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
определяется из формулы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
cos |
|
|
|
m1m2 |
|
n1n2 |
p1 p2 |
|
|
. |
(7) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
m2 |
|
n2 |
p2 |
m2 |
n2 |
p2 |
|
|||||
|
|
|
|
1 |
|
1 |
|
1 |
|
2 |
2 |
2 |
|
|
|
||
Для нахождения острого угла между прямыми числитель правой части формулы следует взять по модулю:
cos |
|
|
m1m2 |
n1n2 |
p1 p2 |
|
|
|
. |
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||
|
|
m2 |
n2 |
p2 |
m2 |
n2 |
p2 |
||||
1 |
1 |
1 |
|
2 |
2 |
2 |
|
|
|||
Условие параллельности двух прямых в пространстве:
m1 |
|
n1 |
|
p1 |
. |
|
|
|
|
||
m2 |
|
n2 |
|
p2 |
|
Условие перпендикулярности двух прямых в пространстве: m1m2 n1n2 p1 p2 0 .
6.Необходимое и достаточное условие расположения двух прямых
водной плоскости (условие компланарности двух прямых):
x2 x1 |
y2 |
y1 z2 |
z1 |
|
|
m1 |
n1 |
p1 |
|
0 . |
(8) |
m2 |
n2 |
p2 |
|
|
|
Замечания:
1)если в определителе все строки пропорциональны, то прямые совпадают;
2)если пропорциональны только вторая и третья строки, то прямые параллельны;
3)если определитель равен нулю, но вторая и третья строки непро-
порциональны, то прямые пересекаются;
4)если определитель не равен нулю, то прямые скрещиваются.
15

7. |
|
|
Расстояние |
|
|
|
|
от |
|
|
|
точки |
|
|
|
|
M0 (x0 ; y0 ; z0 ) |
до |
|
|
прямой |
||||||||||||||||||||||||||||
|
x x1 |
|
y y1 |
|
|
z |
z1 |
|
вычисляется по формуле: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
m1 |
n1 |
|
|
p1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
y |
y |
0 |
|
z |
z |
0 |
|
2 |
|
|
x x |
z |
|
|
z |
0 |
|
2 |
|
|
|
|
x x |
y y |
0 |
|
2 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
0 |
1 |
|
|
|
|
|
|
|
|
1 |
0 |
1 |
|
|
|
|
|
|||||||||||||||
d |
|
|
|
n1 |
|
|
|
p1 |
|
|
|
|
|
|
|
|
|
m1 |
|
|
|
|
|
|
p1 |
|
|
|
|
|
|
|
|
m1 |
|
|
n1 |
|
|
|
|
|
. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m2 |
|
|
n2 |
|
p2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Пример 3.1. Найти направляющий вектор прямой |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x |
y |
|
z |
|
|
1 |
|
0, |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x y 3z 5 0. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Решение. Направляющий вектор находим по формуле (6): |
||||||||||||||||||||||||||||||||||||||||||||||||
Так как по условию A1 |
|
|
2, B1 |
|
1,C1 |
|
|
1, A2 |
|
2, B2 |
1,C2 |
|
|
|
3 , то |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
s |
|
|
|
|
|
|
1 |
|
; |
|
2 |
|
|
1 |
|
; |
|
2 |
|
|
1 |
|
, s |
|
2; 8; 4 . |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 3 |
|
|
2 3 |
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
Ответ: s |
2; |
8; 4 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
Пример 3.2. Составить параметрические и канонические уравнения |
||||||||||||||||||||||||||||||||||||||||||||||||
прямой, проходящей через точку M0 (2; |
|
|
4;5) параллельно прямой, |
||||||||||||||||||||||||||||||||||||||||||||||
заданной уравнениями |
|
x 1 |
|
|
y |
3 |
|
|
z |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Решение. Числа в знаменателях уравнений, |
|
описывающих задан- |
||||||||||||||||||||||||||||||||||||||||||||||
ную прямую, представляют собой координаты направляющего вектора этой прямой. Так как искомая прямая параллельна заданной, то направляющие векторы обеих прямых совпадают.
Следовательно, |
m 2, n 1, p 5 . По условию задачи имеем также: |
|
x0 2, y0 |
4, z0 |
5. |
Тогда система параметрических уравнений искомой прямой: x 2 2t,
y 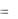 4 t, z 5 5t.
4 t, z 5 5t.
16

Аналогичным образом находим канонические уравнения прямой:
|
|
|
|
x 2 |
|
y 4 |
|
z 5 |
. |
|||||
|
|
|
2 |
|
1 |
|
5 |
|||||||
|
|
|
|
|
|
|||||||||
x 2 2t, |
|
|
|
|
|
|
|
|
|
|
|
|
||
Ответ: y |
4 |
t, |
x 2 |
|
|
y 4 |
z 5 |
. |
||||||
2 |
|
1 |
|
|
5 |
|||||||||
z |
5 |
5t, |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример 3.3. Найти уравнение прямой, проходящей через точку M1( 2;3;4) и перпендикулярной прямым:
x 2 y 1 z |
и |
x |
|
y 2 |
|
z 1 |
. |
|||||
1 |
|
1 |
|
2 |
2 |
|
1 |
|
3 |
|||
|
|
|||||||||||
Решение. Уравнение искомой прямой имеет вид:
x 2 |
|
y 3 |
z 4 |
. |
|
|
|
|
|
|
|
m |
|
n |
p |
||
Найдем m, n и p − координаты направляющего вектора s этой
прямой. Используя условие перпендикулярности прямых, можно записать:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m 1 |
n ( |
1) |
|
p 2 |
0, |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m 2 |
n 1 |
|
p 3 |
0. |
|
|
|
|||||||||||
|
|
Данную систему можно переписать в виде |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
n |
2 |
0, |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
p |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
m |
|
n |
|
3 |
0. |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
p |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Отсюда |
|
m |
|
|
|
|
|
5 |
, |
n |
1 |
, т. е. m : n : p |
5 :1: 3 , поэтому m 5t, |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
p |
|
|
|
3 |
|
p |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
n |
t, p |
|
3t, |
где t число. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Уравнения искомой прямой есть |
x |
2 |
|
|
y |
3 |
|
|
z 4 |
или |
||||||||||||||||||||||||||||||
|
|
|
|
t |
|
|
|
3t |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5t |
|
|
|
|
|
||||
|
x |
2 |
|
|
y |
3 |
|
|
|
z |
4 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
5 |
|
|
1 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Ответ: |
|
x |
2 |
|
|
|
y |
3 |
|
z 4 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
17
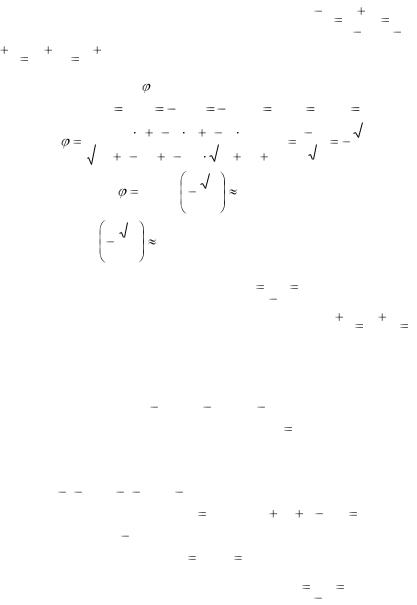
|
Пример 3.4. |
|
Найти угол между прямыми |
|
x |
1 |
|
y |
2 |
|
|
z |
и |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x 1 |
y 11 z |
6 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Решение. Найдем cos |
по формуле (7). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
В нашем случае, m1 |
2, n1 |
1, p1 |
2, |
m2 |
1, |
|
|
n2 |
|
2, p2 |
1 и |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
cos |
|
|
|
|
2 1 |
( 1) 2 |
|
|
( 2) 1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
6 |
|
, |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|||||||
|
|
|
22 |
|
( 1)2 |
( 2)2 |
|
12 |
22 |
12 |
|
|
|
3 6 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
следовательно, угол |
|
|
|
arccos |
|
6 |
|
|
106 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Ответ: arccos |
6 |
|
|
106 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Пример 3.5. В уравнениях прямой |
|
x |
|
y |
|
|
z |
|
определить пара- |
||||||||||||||||||||||||||||||||||||||
|
2 |
|
3 |
|
|
n |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
метр n так, чтобы эта прямая пересекалась с прямой |
x |
1 |
|
|
y 5 |
|
|
z |
, |
|||||||||||||||||||||||||||||||||||||||
|
3 |
|
|
|
2 |
|
|
1 |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
и найти точку их пересечения.
Решение. Для нахождения параметра n используем условие пересечения двух прямых:
|
|
|
x2 |
x1 |
y2 y1 |
z2 |
z1 |
|
|
|
|
|
|
|
|
|
|
|
m1 |
|
|
n1 |
p1 |
|
|
0. |
|
|
|
|
|
|
|
|
m2 |
|
|
n2 |
p2 |
|
|
|
|
|
|
|
|
Из (8) следует: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( 5) |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
||
|
0 ( 1) 0 |
|
|
|
|
|
|
|
|
|
|
||||
|
3 |
2 |
1 |
|
0 или 2n |
10 3 |
15n |
0 , |
|||||||
|
2 |
3 |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13n 13 , n 1 . |
|
|
|
|
|
|
|
|
|||
Следовательно, уравнения искомой прямой: |
x |
y |
z |
. |
|||||||||||
2 |
|
3 |
|
1 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
18

Для вычисления координат точки пересечения прямых выразим x
и |
y через z |
из уравнения |
x |
|
y |
|
|
z |
: x |
2z , |
y |
|
3z . |
Подставляя |
|||||||||||||
2 |
|
|
3 |
|
|
1 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
их значения в равенство |
x |
1 |
|
|
y 5 |
, имеем |
|
|
2z |
1 |
|
3z |
5 |
, отсюда |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
3 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
2 |
|
|
||||||
z |
1. Зная z , находим x и y : x |
|
2z |
|
|
|
2 , |
y |
|
|
3z |
|
|
3 . |
|
|
|||||||||||
|
Следовательно, M (2; 3;1) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Ответ: n |
1 , M (2; 3;1) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Пример 3.6. Прямая задана каноническими уравнениями |
||||||||||||||||||||||||||
|
|
|
|
x |
2 |
|
|
y |
1 |
|
z |
3 |
. |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
3 |
|
|
5 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||
Составить общие уравнения этой прямой.
Решение. Канонические уравнения прямой можно записать в виде системы двух независимых уравнений:
|
|
|
|
x |
2 |
|
y |
1 |
, |
|
|
|
|
|
|
3 |
|
|
|
5 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
x |
2 |
|
z |
3 |
, |
|
|
|
|
|
|
3 |
|
|
|
1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
отсюда |
5x |
3y 13 0, |
Получили общие уравнения прямой, которая |
|||||||||
|
x 3z 11 0. |
|
|
|
|
|
|
|
|
|
|
|
теперь |
задана пересечением 2-х |
плоскостей, |
одна |
из |
которых |
|||||||
5x 3y |
13 |
0 параллельна оси |
Oz , а другая x |
3z |
11 |
0 парал- |
||||||
лельна оси Oy .
Ответ:
5x 3y 13 0, x 3z 11 0.
Пример 3.7. Составить параметрические уравнения прямой, проведенной через точку M0 (5; 1; 4) параллельно оси Ox .
Решение. Вектор, параллельный оси Ox , имеет координаты y 0, z 0 . В качестве направляющего вектора прямой берем единич-
19
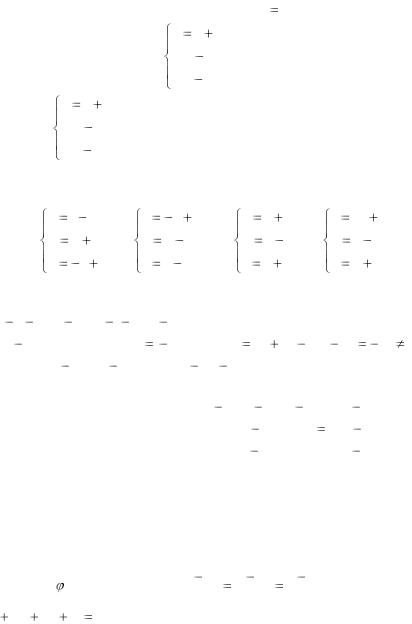
ный вектор, направленный по оси Ox , т. е. s (1;0;0) . Тогда парамет- x 5 t,
рические уравнения прямой: y 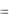 1, z
1, z 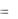 4.
4.
x 5 t,
Ответ: y 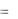 1, z
1, z 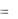 4.
4.
Пример 3.8. Исследовать взаимное расположение двух прямых в каждом из следующих случаев:
x 1 2t, |
x |
4 3t, |
x 6 2t, |
x 10 4t, |
|
1) y 2 5t, и |
y 2 t, |
2) y 5 t, и |
y 3 2t, |
||
z |
3 4t |
z 5 2t; |
z 3 2t |
z 7 4t. |
|
Решение. 1) Из необходимого и достаточного условия расположения двух прямых (8) получим:
|
4 1 |
2 |
2 |
5 ( 3) |
|
5 |
0 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
5 |
|
4 |
|
2 |
5 |
4 |
|
|
50 |
16 |
120 |
20 |
|
74 |
0 . |
||
|
3 |
1 |
2 |
|
3 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
||
Следовательно, прямые скрещиваются. |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
6 |
|
3 |
5 |
7 |
3 |
|
4 |
2 |
4 |
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
||||||||
2) Так |
как |
в |
определителе |
|
2 |
|
|
|
1 |
|
2 |
|
2 |
1 |
2 |
все |
|||
|
|
|
|
|
|
|
|
4 |
|
|
|
2 |
|
4 |
|
4 |
2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
строки пропорциональны, то прямые совпадают.
Ответ: 1) прямые скрещиваются; 2) прямые совпадают.
4. Прямая и плоскость в пространстве
1. Угол |
между прямой |
x x0 |
|
y y0 |
|
z z0 |
и плоскостью |
m |
|
n |
|
p |
|||
|
|
|
|
|
Ax By Cz D 0 определяется из соотношения:
20
