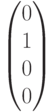- •Оглавление
- •Об информационно-библиотечной культуре
- •Информация, сведения, данные, знания
- •Появление и развитие информатики
- •Информатика и библиотековедение
- •Измерение и меры информации. Энтропия
- •Лекция 2: Документальные потоки и коммуникация Неформальные и формальные каналы коммуникации
- •Библиотеки, библиография и библиографическое описание
- •Библиотечная и информационная деятельность
- •Тенденции развития основных видов документов
- •Закономерности роста и старения
- •Оценка значимости (влиятельности) ученых и журналов
- •Закон рассеяния статей конкретной тематики по журналам
- •Лекция 3: Инструменты традиционного и сетевого информационного поиска Предыстория и сущность
- •Процедуры и понятия
- •Координатное индексирование
- •Цитирование, библиографическое сочетание, социтирование
- •Рубрикаторы информационных изданий
- •Лекция 4: Электронные ресурсы информации Электронные издания
- •Информационные ресурсы, структуры и инфраструктура
- •Информационные продукты и услуги
- •Лекция 5: Информатизация и информационное общество Основные понятия и проблемы становления информационного общества. Информатизация как процесс перехода к информационному обществу
- •Возникновение, этапы развития и технологические аспекты информатизации
- •Положительные и отрицательные последствия информатизации
- •Программы информатизации
- •Программы информатизации России
- •Электронное правительство
- •Контрольные вопросы
- •Лекция 6: Информационные технологии Представления информации Сообщение как материальная форма представления информации
- •Формы сообщений (сигналы, изображения, знаки, языковые сообщения)
- •Основные понятия теории формальных языков
- •Модели источников сообщений. Конечный вероятностный источник сообщений
- •Кодирование сообщений источника и текстов. Равномерное кодирование. Дерево кода
- •Префиксные коды
- •Необходимые и достаточные условия существования префиксного кода с заданными длинами кодовых слов. Неравенство Крафта
- •Методы построения кодов. Код Фано
- •Избыточность кодирования. Нижняя граница средней длины кодирования
- •Оптимальное кодирование, свойства оптимальных кодов, построение оптимальных кодов методом Хафмена
- •Лекция 7: Передача информации Модель процесса передачи. Двоичный симметричный канал
- •Способы повышения надежности передачи сообщений
- •Принципы обнаружения и исправления ошибок с использованием кодов
- •Расстояние Хеминга и корректирующие возможности кодов
- •Оценки верхних границ корректирующих способностей кодов
- •Особенности векторных пространств над конечным полем gf(2). Линейный групповой код
- •Построение линейного кода по заданной порождающей матрице
- •Декодирование линейного кода по синдрому
Декодирование линейного кода по синдрому
Путь ![]() -матрица размера
-матрица размера ![]() и
ранга
и
ранга![]() над
полем
над
полем![]() .
Этаматрица задает
линейное отображение
.
Этаматрица задает
линейное отображение ![]() пространства
пространства![]() впространство
впространство ![]() по формуле
по формуле ![]() .Ядро этого
линейного отображения или множество
решений уравнения
.Ядро этого
линейного отображения или множество
решений уравнения ![]() ,
образующее подпространство пространства
,
образующее подпространство пространства![]() ,
являетсялинейным
кодом.
Можно рассмотреть разбиение пространства
,
являетсялинейным
кодом.
Можно рассмотреть разбиение пространства ![]() на
классы равнообразности. В одинкласс входят
все элементы
на
классы равнообразности. В одинкласс входят
все элементы ![]() ,
которые при отображении
,
которые при отображении![]() переходят
в один и тот же элемент пространства
переходят
в один и тот же элемент пространства![]() .
Элемент пространства
.
Элемент пространства![]() ,
в который переходят все элементы одного
класса, называется
синдромом.Pис.7.8 иллюстрирует разбиение пространства
,
в который переходят все элементы одного
класса, называется
синдромом.Pис.7.8 иллюстрирует разбиение пространства ![]() на
классы равнообразности.
на
классы равнообразности.
Отображение ![]() является
отображением на всепространство
является
отображением на всепространство ![]() .
Для систематической матрицы H это
практически очевидно. Действительно,
для любого
.
Для систематической матрицы H это
практически очевидно. Действительно,
для любого![]() можно
найти (построить)
можно
найти (построить)![]() ,
такой, что
,
такой, что![]() .
.

Рис. 7.8. Разбиение пространства Bn на классы равнообразности
Произведение ![]() называется
синдромом[29], [33].
Фактически, синдромом вектора
называется
синдромом[29], [33].
Фактически, синдромом вектора ![]() является
образ этого вектора при отображении
-
является
образ этого вектора при отображении
-![]() .
Все векторы
.
Все векторы![]() ,
имеющие один синдром, образуюткласс.
Так как синдром
,
имеющие один синдром, образуюткласс.
Так как синдром ![]() имеетразмерность
имеетразмерность ![]() ,
всего существует
,
всего существует![]() классов
(если проверочнаяматрица имеетранг
классов
(если проверочнаяматрица имеетранг ![]() ,
в частности, еслиматрица
,
в частности, еслиматрица ![]() имеетсистематический вид).
Из определения линейного кода следует,
что класс,
которому соответствует нулевой синдром,
является кодом
имеетсистематический вид).
Из определения линейного кода следует,
что класс,
которому соответствует нулевой синдром,
является кодом ![]() .
Каждыйкласс
.
Каждыйкласс ![]() ,
отличный от кода, порождается
"сдвигом"
,
отличный от кода, порождается
"сдвигом"![]() кода
кода![]() на
один из векторов
на
один из векторов![]() класса
класса![]() .
Действительно, если
.
Действительно, если![]() .,
то есть
.,
то есть![]() ,
тогда
,
тогда![]() и,
следовательно,
и,
следовательно,![]() и
и![]() ,
где
,
где![]() -
кодовоеслово.
Таким образом, любой некодовый вектор,
имеющий синдром
-
кодовоеслово.
Таким образом, любой некодовый вектор,
имеющий синдром ![]() ,
можно представить в виде суммы кодового
вектора и вектора, имеющего
синдром
,
можно представить в виде суммы кодового
вектора и вектора, имеющего
синдром![]() .Представление такого
вида не является единственным.
Некодовый вектор
.Представление такого
вида не является единственным.
Некодовый вектор ![]() в
этой сумме можно рассматривать
каквектор ошибок,
произошедших в тех разрядах кодового
слова
в
этой сумме можно рассматривать
каквектор ошибок,
произошедших в тех разрядах кодового
слова ![]() ,
в которых соответствующие компоненты
вектора
,
в которых соответствующие компоненты
вектора![]() равны
1. Из всех векторов ошибок, имеющих один
синдром, наиболее вероятным
являетсявектор
равны
1. Из всех векторов ошибок, имеющих один
синдром, наиболее вероятным
являетсявектор ![]() (векторы)
с минимальным весом (числом
единичныхкомпонент).
Такой вектор (векторы)
называется лидером класса.
(векторы)
с минимальным весом (числом
единичныхкомпонент).
Такой вектор (векторы)
называется лидером класса.
Алгоритм декодирования
заключается в следующем. Если
получен вектор ![]() и
и![]() ,
считаем, что ошибкам соответствует
наиболее вероятныйвектор из
класса
,
считаем, что ошибкам соответствует
наиболее вероятныйвектор из
класса ![]() ,
то есть лидер
,
то есть лидер![]() класса
класса![]() .
Тогдадекодирование осуществляется
ввектор
.
Тогдадекодирование осуществляется
ввектор ![]() ,
получающийся из принятого вектора
удалением лидера.
,
получающийся из принятого вектора
удалением лидера.
Рассмотрим
пример построения кода по заданной
проверочной матрице и декодирования
полученного сообщения по синдрому.
Пусть дана проверочная матрица  .
Запишем уравнение для определения
кодовых векторов (слов) для данной
матрицы:
.
Запишем уравнение для определения
кодовых векторов (слов) для данной
матрицы:
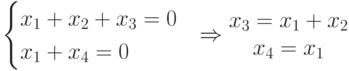
![]() и
и ![]() которые
можно рассматривать как информационные
разряды, задаются произвольно (всего 4
варианта 00, 01, 10, 11), а проверочные
разряды
которые
можно рассматривать как информационные
разряды, задаются произвольно (всего 4
варианта 00, 01, 10, 11), а проверочные
разряды![]() и
и![]() определяются
через
определяются
через![]() и
и![]() .
В итоге все кодовые слова определяются
из выражения
.
В итоге все кодовые слова определяются
из выражения

где ![]() и
и![]() -
информационные разряды, а
-
информационные разряды, а -
порождающаяматрица,
столбцами которой являются кодовые
векторы.
-
порождающаяматрица,
столбцами которой являются кодовые
векторы.
Кодовые слова, рассматриваемые как векторы-столбцы, образуют матрицу кода

Расстояние кода ![]() равно
минимальному весу ненулевого слова
равно
минимальному весу ненулевого слова![]() .
.
Найдем
смежные классы, которые состоят из
векторов пространства ![]() ,
имеющих одинаковый синдром, и выберем
в каждом классе лидера (вектор из
класса с минимальным весом).
,
имеющих одинаковый синдром, и выберем
в каждом классе лидера (вектор из
класса с минимальным весом).
Синдромом
является любое возможное значение произведения ![]() .
.
В
данном случае имеется 4 синдрома: ![]() .Каждому
синдрому соответствует смежныйкласс,
синдром
.Каждому
синдрому соответствует смежныйкласс,
синдром ![]() соответствует
коду. Смежные классы (столбцы матриц)
для каждого синдрома и выбранные лидеры
приведены в таблице.
соответствует
коду. Смежные классы (столбцы матриц)
для каждого синдрома и выбранные лидеры
приведены в таблице.
|
Синдром |
|
|
|
|
|
Класс смежности |
|
|
|
|
|
Лидер |
|
|
|
|
В третьем смежном классе - два потенциальных лидера с весом (нормой), равным 1. Один из них выбирается в качестве лидера произвольно.
Рассмотрим
на этом примере процесс декодирования
полученного вектора (слова) с использованием
синдромов. Пусть передавался
кодовый вектор  и
в процессе переачи произошла ошибка в
первом разряде. Это означает, что на
приемном конце был полученвектор
и
в процессе переачи произошла ошибка в
первом разряде. Это означает, что на
приемном конце был полученвектор  ,
полученный из переданного вектора
,
полученный из переданного вектора в
результате добавления вектора
ошибки
в
результате добавления вектора
ошибки (ошибка
в первом разряде). Определим синдром,
вычисливпроизведение
(ошибка
в первом разряде). Определим синдром,
вычисливпроизведение ![]() .
В данном случае получим
.
В данном случае получим![]() .
Это означает, что полученныйвектор
.
Это означает, что полученныйвектор ![]() водит
в четвертый смежныйкласс (см.
таблицу). Лидером этого смежного класса
является вектор
водит
в четвертый смежныйкласс (см.
таблицу). Лидером этого смежного класса
является вектор  ,
соответствующий данному синдрому.
Вычитая (добавляя) лидер к принятому
вектору, производимдекодирование
,
соответствующий данному синдрому.
Вычитая (добавляя) лидер к принятому
вектору, производимдекодирование 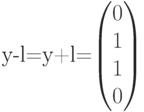 В
данном случаедекодирование выполнено
правильно.
В
данном случаедекодирование выполнено
правильно.