31.5. Дискретные случайные величины. Функция

распределения. Числовые характеристики

случайных величин

Случайной величиной (СВ), связанной с данным опытом, называется величина, которая при каждом осуществлении этого опыта принимает то или иное значение, причем заранее неизвестно, какое именно.

Случайные величины обозначают прописными буквами ла­тинского алфавита X, Y, Z, U, …, а значения, принимаемые ими, –соответствующими строчными буквамиx,y,z,u, …

Каждой случайной величине Xсоответствует некоторое множество чисел, называемое множеством значений, которые может принимать величинаX.

Любое правило, устанавливающее связь между возможными значениями случайной величины и их вероятностями, называет­ся законом распределенияслучайной величины.

Наиболее удобными для изучения являются так называемые дискретные случайные величины. Они характеризуются тем, что могут принимать лишь конечное или счетное множество значений.

Будем говорить, что задана дискретная случайная величина X, если указано конечное или счетное множество чисел

x₁,x₂,x₃,x₄,x₅, …

и каждому из этих чисел x_iпоставлено в соответствие некоторое положительное числоp_i(i  N), причем сумма всехp_iравна 1.

Числа x₁,x₂, … называютсявозможными значениямислучайной величиныX, а числаp₁,p₂, … – вероятностями этих значений:

Итак, дискретная случайная величина задается таблицей вида:

X	x1	x2	x3	…	xn
P	p1	p2	p3	…	pn

с условием, что числа p₁,p₂, … положительны и

Эту таблицу обычно называют законом распределения дискретной случайной величины X.

Если множество возможных значений случайной величины Xбесконечно (счетно), то рядp₁+p₂+ … сходится и его сумма равна единице.

Для наглядности закон распределения дискретной случай­ной величины изображают графически, для чего в прямоуголь­ной системе координат строят точки (x_i,p_i) и соединяют их по­следовательно отрезками прямых. Получающаяся при этом ло­маная линия называетсямногоугольником распределения слу­чайной величиныX.

Каждой случайной величине Xможно сопоставить функциюF, определенную на всей числовой оси. При любомx₀значениеF(x₀) задается равенством

т. е. F(x₀) есть вероятность того, что случайная величинаXпримет значение меньшее, чемx₀.

Функция Fназывается функцией распределенияслучайной величиныX.

Все значения функции распределения F(x) принадлежат отрезку [0; 1], т. е.

Функция F(x) неубывающая, т. е. если

Функция F(x) в точкеx₀непрерывна слева, т. е.

Если функция распределения F(x) задана, то вероятность событиявычисляется по формуле

Вероятность того, что случайная величина Xпримет определенное значениеx₀, выражается через функцию распределения по формуле

Характеристикой среднего значения случайной величины служит математическое ожидание.

Пусть случайная величина Xпринимает значенияx₁,x₂, …,x_nс вероятностямиp₁,p₂, …,p_nсоответственно.

Математическим ожиданиемM(X) дискретной случайной величиныXназывается сумма произведений всех возможных значений величиныXна соответствующие вероятности:

В случае, когда предполагается, что полученный числовой ряд абсолютно сходится.

Основные свойства математического ожидания

1.где

2.где

3.

4. (для независимых случайных ве­личин).

5.

Математическое ожидание не дает полной характеристики закона распределения случайной величины. Характеристиками рассеивания возможных значений случайной величины вокруг математического ожидания служат, в частности, дисперсия и среднее квадратическое отклонение.

ДисперсиейD(X) дискретной случайной величиныXназывается математическое ожидание квадрата отклонения случайной величиныXот ее математического ожидания:

Дисперсию удобно вычислять по формуле

Основные свойства дисперсии

Пусть – независимые случайные величины.

1.где

2.где

3.

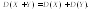
4.

Средним квадратическим отклонениемслучайной величиныXназывается корень квадратный из дисперсии:

Для более подробного описания свойств случайной величины Xрассмотрим и некоторые другие ее характеристики.

Модой M₀ дискретной случайной величиныXназывается ее наиболее вероятное значение.

Медианойслучайной величиныXназывается такое ее значениеM_e, для которого

Начальным моментом порядка случайной величиныназывается математическое ожидание случайной величиныгде– натуральное число:

Математическое ожидание и дисперсию случайной величи­ны X можно выразить через начальные моменты порядка 1 и 2:

Центральным моментом порядка случайной величиныX называется математическое ожидание величины

Пример 1. По мишени стреляют один раз с вероятностью попадания 0,6. Случайная величина X – число попаданий. Найти закон распределения этой случайной величины.

Решение. Очевидно, X может принимать только два значения: 1 и 0, причем их вероятности равны соответственно 0,6 и 0,4. Действительно, при выстреле возможны два исхода: попадание (тогда X = 1) и промах (тогда X = 0); вероятности этих событий суть 0,6 и 1 – 0,6 = 0,4. В итоге получим следующую таблицу:

X	1	0
P	0,6	0,4

Пример 2. Дискретная случайная величина X задана законом распределения:

X	1	2	4	6
P	0,2	0,1	0,5	0,2

Построить многоугольник распределения.

Решение. Построим прямоугольную систему координат, причем по оси абсцисс будем откладывать возможные значения x_i, а по оси ординат – соответствующие вероятности Построим точкиM₁(1; 0,2), M₂(2; 0,1), M₃(4; 0,5), M₄(6; 0,2). Соединив эти точки отрезками прямых, получим искомый многоугольник распределения (рис. 31.4).

Рис. 31.4

Пример 3. Найти функцию распределения дискретной случайной величины Х из примера 2. Используя функцию распределения, вычислить вероятности событий: X < 2;

Решение. Используя данные из таблицы, получим функцию распределения:

График функции F(x) представлен на рис. 31.5.

Рис. 31.5

Пример 4. В денежной лотерее разыгрывается 1 выигрыш в 1000 денежных единиц, 10 выигрышей по 100 денежных единиц и 100 выигрышей по 1 денежной единице при общем числе билетов 10 000. Найти закон распределения случайного выигрыша X для владельца одного лотерейного билета и математическое ожидание выигрыша X.

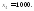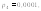
Решение. Возможные значения для X: Вероятности их будут: 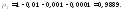Следовательно, закон распределения выигрыша X может быть задан таблицей:

X	0	1	100	1000
P	0,9889	0,01	0,001	0,0001

Найдем математическое ожидание выигрыша X. Используя полученную таблицу, имеем:

Пример 5. Случайная величина X задана законом распределения:

X	1	3	6	7	9
P	0,2	0,2	0,3	0,1	0,2

Найти D(X).

Решение. Имеем:

Таким образом, закон распределения случайной величины выразится таблицей:

(X – M(X))2	16,81	4,41	0,81	3,61	15,21
P	0,2	0,2	0,3	0,1	0,2

Отсюда получаем