33.5. Приближенное решение обыкновенных

дифференциальных уравнений

Приближенные методы решения обыкновенных дифференциальных уравнений в зависимости от формы представления решения можно разделить на две группы: 1) аналитические методы, дающие приближенное решение дифференциального уравнения в виде аналитического выражения; 2) численные методы, дающие приближенное решение в виде таблицы.

Интегрирование дифференциальных уравнений

с помощью рядов

Пусть дано дифференциальное уравнение

(33.27)

с начальным условием

Метод последовательного дифференцирования состоит в том, что решение уравнения (33.27) ищут в виде ряда Тейлора

где а производныенаходят последовательным дифференцированием уравнения (33.27) и подстановкой в результат дифферен-цирования начальных данных и всех остальных найденных значений производных. С помощью рядов Тейлора аналогично можно интегрировать уравнения высших порядков и системы обыкновенных дифференциальных уравнений.

Метод неопределенных коэффициентов состоит в том, что решение уравнения (33.27) ищут в виде степенного ряда

с неопределенными коэффициентами которые находят путем подстановки ряда в уравнение (33.27) и приравниванием коэффициентов при одинаковых степенях разностив обеих частях полученного равенства. Аналогично можно интегрировать уравнения высших порядков.

Численное интегрирование

дифференциальных уравнений

Пусть требуется решить задачу Коши:

(33.28)

где – функция, непрерывно дифференцируемая впрямоугольнике .Выбрав достаточно малый шаг интегрирования h, построим систему равноотстоящих точек (узлов) где

Суть метода Эйлера состоит в том, что за приближенное значение решения уравнения в точкеберется ординататочки пересечения прямой

(33.29)

с прямой т. е.

(33.30)

Отрезки (33.29) образуют ломаную, называемую ломаной Эйлера. Она является приближенным решением задачи Коши (33.28), аппроксимирующим искомую интегральную кривую уравнения (32.27).

Пример 1. Методом последовательного дифференцирования найти частное решение дифференциального уравнения удовлетворяющее начальным условиям

Решение. Будем искать решение данного уравнения в виде ряда Маклорена

Подставляя в уравнение начальные условия, получим

Дифференцируя исходное уравнение, последовательно находим:

……………….…………………………………………

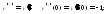
Подставляя найденные значения производных в ряд Маклорена, получаем

Следовательно, искомое частное решение уравнения имеет вид:

Пример 2. С помощью метода неопределенных коэффициентов найти первые четыре члена разложения в ряд частного решения дифференциального уравнения удовлетворяющего начальному условию

Решение. Будем искать решение уравнения в виде степенного ряда

Дифференцируем его:

Согласно начальному условию, Подставляя выражения дляy, в исходное уравнение, получим

или

Приравнивая коэффициенты при одинаковых степенях разности в обеих частях полученного равенства, имеем систему уравнений для определения коэффициентов

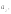
Решая эту систему, найдем Следовательно, искомое частное решение уравнения запишется в виде:

Пример 3. Методом Эйлера найти численное решение задачи Коши на отрезкеполагая

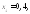
Решение. Находим последовательные значения аргумента: По формуле (33.30) вычисляем соответствующие значения искомой функции:

Таким образом, получаем следующую таблицу:

0 1 2 3 4 5	0 0,1 0,2 0,3 0,4 0,5	1 1 0,98 0,9408 0,8844 0,8136	1 0,990049… 0,960789… 0,913931… 0,852143… 0,778800…

В последнем столбце таблицы для сравнения помещены значения точного решения задачи Коши.

приложения