32.5. Элементы теории корреляции. Выборочное

уравнение регрессии, оценка регрессионных

характеристик

Пусть X,Y– случайные величины. Статистическая зависимость, при которой изменение одной величины влечет изменение среднего значения другой, называетсякорреляционной.

Условным среднимназывается среднее арифметическое значениеYприX = x.

Если каждому значению xсоответствует одно значение условной средней, то зависимость условной среднейотxявляется функцией отx.

Корреляционной зависимостьюYотXназывается функциональная зависимость условной среднейотx

(32.1)

Уравнение (32.1) называется уравнением регрессииYнаX. ФункцияназываетсярегрессиейYнаX, а ее график – линией регрессииYнаX.

Если обе линии регрессии YнаXиXнаY– прямые, то корреляцию называютлинейной.

Корреляционная зависимость между Xи Yобычно задается с помощью корреляционной таблицы.

X	Y
	y1	y2	…	yl
x1	n11	n12	…	n1l
x2	n21	n22	…	n2l
…	…	…	…	…
xk	nk1	nk2	…	nkl

Здесь, например, частота n₁₂означает, что пара (x₁,y₂)встречается n₁₂ раз, Не исключается, что некоторые частоты могут быть равны нулю. Еслиk = l и все частоты приприто имеем случайпарной корреляции.

Выборочный коэффициент корреляции определяется по формуле

где n– объем выборки;

–выборочные средние;

–выборочные средние квадратические отклонения.

Наиболее простыми и важными случаями кривых регрессий являются прямые линии.

Уравнение прямой линии регрессии YнаXимеет вид:

где – условная средняя;

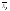
–выборочные средние признаков X и Y;

–выборочный коэффициент корреляции;

–выборочные квадратические отклонения признаков X и Y.

Уравнение прямой линии регрессии XнаYимеет вид:

Величины иназываютсялинейными коэффициентами регрессии и обозначаются соответственно и

или

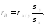
Квадрат коэффициента линейной корреляции дает коэффициент детерминации, который измеряет долю вариацииY, объясняемую влияниемX, и наоборот.

Если данные наблюдений над признаками XиYзаданы в виде корреляционной таблицы с равноотстоящими вариантами, то целесообразно перейти кусловным вариантам

где c₁, c₂ – варианты признака (обычно за условные нули c₁ и c₂ принимают варианты с наибольшими частотами);

h₁,h₂– разности между соседними вариантами признаковXиY.

В условных вариантах выборочный коэффициент корреляции

где можно вычислить по формулам:

Если распределение случайных величин XиYблизко к нормальному, то можно приближенно считать выборочный коэффициент линейной корреляцииr_Bтакже нормальной величиной с

Для коэффициента корреляции rгенеральной совокупности доверительный интервал определяется неравенством

где – доверительная вероятность, анаходится из равен­ства

Аналогичные оценки имеются и для коэффициентов регрессии.

Пусть двумерная генеральная совокупность (X,Y) распределена нормально. Из этой совокупности извлечена выборка объемаnи по ней найден выборочный коэффициент корреляцииТребуется проверить нулевую гипотезуо равенстве нулю генерального коэффициента корреляции.

Если нулевая гипотеза принимается, то это означает, что XиYнекоррелированы, в противном случае – коррелированы.

Правило.Чтобы при уровне значимостипроверить нулевую гипотезу о равенстве нулю генерального коэффициента корреляции нормальной двумерной случайной величины при конкурирующей гипотезенадо вычислить наблюдаемое значение критерия

и по таблице критических точек распределения Стьюдента (прил. 8), по заданному уровню значимости и числу степеней свободынайти критическую точкудвусторонней критической области. Если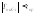– нет оснований отвергнуть нулевую гипотезу. Если– нулевую гипотезу отвергают.

Пример 1. В результате 10 независимых опытов над системой (X, Y) получены точки: (2,1; 3,0), (2,1; 2,8), (2,0; 3,0), (2,5; 2,0), (2,8; 1,8), (2,2; 2,5), (3,2; 1,5), (3,2; 1,1), (3,2; 1,0), (4,7; 1,3). Найти выборочный коэффициент корреляции.

Решение. Для удобства вычислений составим расчетную таблицу:

Номер опыта	xk	yk	xkyk
1 2 3 4 5 6 7 8 9 10	2,1 2,1 2,0 2,5 2,8 2,2 3,2 3,2 3,2 4,7	3,0 2,8 3,0 2,0 1,8 2,5 1,5 1,1 1,0 1,3	6,30 5,88 6,0 5,0 5,04 5,50 4,80 3,52 3,20 6,11	4,41 4,41 4,00 6,25 7,84 4,84 10,24 10,24 10,24 22,09	9,00 7,84 9,00 4,00 3,24 6,25 2,25 1,21 1,00 1,69
Сумма	28	20	51,35	84,56	45,48

Далее найдем:

Выборочный коэффициент корреляции найдем по формуле

Так как модуль коэффициента корреляции близок к 1, то зависимость между X и Y можно считать близкой к линейной, причем корреляция отрицательная (с возрастанием X величина Y в среднем убывает).

Пример 2. Найти выборочные уравнения регрессии Y на X и X на Y случайных величин из примера 1.

Решение. Используя результаты вычислений в примере 1, имеем:

После упрощений получаем:

Если функция f в (32.1) линейна по x, т. е.

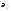то для определения параметров иудобно использовать следующую систему уравнений с двумя неизвестнымии

(32.2)

Пример 3. В книге «Основы химии» Д. И. Менделеева приводятся данные о растворимости азотнокислого натрия в зависимости от температуры воды. В 100 частях воды растворяется следующее число условных частейпри соответствующих температурах:

Температура, C	0	4	10	15	21	29	36	51	68
Количество	66,7	71,0	76,3	80,6	85,7	92,9	99,4	113,6	125,1

Предполагая, что количество (Y), которое растворяется в 100 частях воды, зависит линейно от температуры (X) раствора, найти параметры a и b в формуле по методу наименьших квадратов.

Решение. Для нахождения параметров a и b по методу наименьших квадратов необходимо решить систему уравнений (32.2), в которой в этом случае x_i – температура раствора; y_i – количество азотнокислого натрия, которое растворяется в 100 л воды при данной температуре; Коэффициенты этой системы рассчитаем по следующей схеме:

xi	yi		xiyi
0 4 10 15 21 29 36 51 68	66,7 71,0 76,3 80,6 85,7 92,9 39,4 113,6 125,1	0 16 100 225 441 841 1296 2601 4624	0 284,0 763,0 1209,0 1799,7 2694,1 3578,4 5793,6 8506,8
Сумма 234	811,3	10144	24628,6

Для определения a и b необходимо решить следующую систему двух уравнений с двумя неизвестными:

В результате вычислений получаем: Следовательно, зависимостьy от x имеет вид

Пример 4. Распределение 40 заводов области по количеству ремонтных слесарей l и числу станко-смен m представлено следующей корреляционной таблицей:

m	l							ny
	10–15	15–20	20–25	25–30	30–35	35–40
0–0,2	4						4
0,2–0,4	2	2					4
0,4–0,6			2				2
0,6–0,8		6		4	4		14
0,8–1,0					6	6	12
1,0–1,2						4	4
nx	6	8	2	4	10	10	40

Составить уравнение прямой регрессии.

Решение. За значение признаков примем середины интервалов и составим корреляционную таблицу в условных вариантах, приняв в качестве ложных нулей и(Эти варианты имеют частоту, равную 4, и находятся в середине корреляционной таблицы).

u	v							nu
	–3	–2	–1	0	1	2
–3	4						4
–2	2	2					4
–1			2				2
0		6		4	4		14
1					6	6	12
2						4	4
nv	6	8	2	4	10	10	40

Найдем искомый коэффициент корреляции:

Вычислим

Подставим полученные значения в уравнение регрессии:

Пример 5. По выборке извлеченной из двумерной нормальной генеральной совокупности (X, Y), найден выборочный коэффициент корреляции По уровню значимости 0,05 проверить нулевую гипотезу о равенстве нулю генерального коэффициента корреляции при конкурирующей гипотезе:

Решение. Найдем наблюдаемое (эмпирическое) значение критерия:

Конкурирующая гипотеза имеет вид поэтому критическая область – двусторонняя.

По таблице критических точек распределения Стьюдента (прил. 8), по уровню значимости и числу степеней свободынаходим критическую точку двусторонней критической области

Так как – отвергаем нулевую гипотезу о равенстве нулю генерального коэффициента корреляции. Другими словами, коэффициент корреляции значимо отличается от нуля. Таким образом,X и Y коррелированны.