Матем 2

Решенные задачи:

Задачи 17.25-17.32: С помощью признаков сравнения исследовать, сходится или расходится ряд:

17.25. Общий член ряда имеет вид .

_{Сравним ряд с гармоническим расходящимся рядом,}

ряд сходится по признаку сравнения, так как нет конечного предела, отличного от нуля.

17.26. Общий член ряда имеет вид .

_{Сравним ряд с гармоническим расходящимся рядом,}

ряд сходится по признаку сравнения, так как нет конечного предела, отличного от нуля.

17.27. Общий член ряда имеет вид .

_{Члены данного ряда не превосходят соответствующих членов сходящегося геометрического ряда с общим членом}

ряд сходится по признаку сравнения.

17.28. Общий член ряда имеет вид .

_{Сравним данный ряд с гармоническим. Так как при n > 1 имеем ln (n + 1) < n, то 1/ln (n + 1) > 1/(n + 1), т.е. члены данного ряда, начиная со второго, больше соответствующих членов расходящегося гармонического ряда, а поэтому данный ряд также расходится.}

17.29. Общий член ряда имеет вид .

_{Сравним ряд с гармоническим расходящимся рядом,}

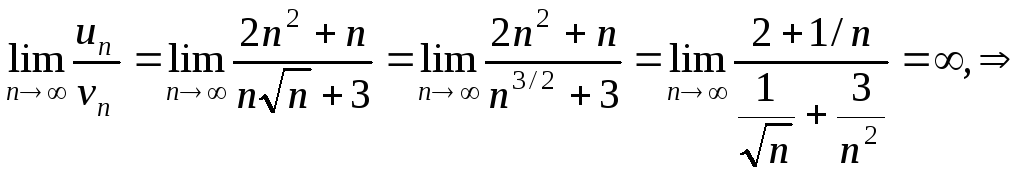ряд сходится по признаку сравнения, так как нет конечного предела, отличного от нуля.

17.30. Общий член ряда имеет вид .

_{Сравним ряд с гармоническим расходящимся рядом,}

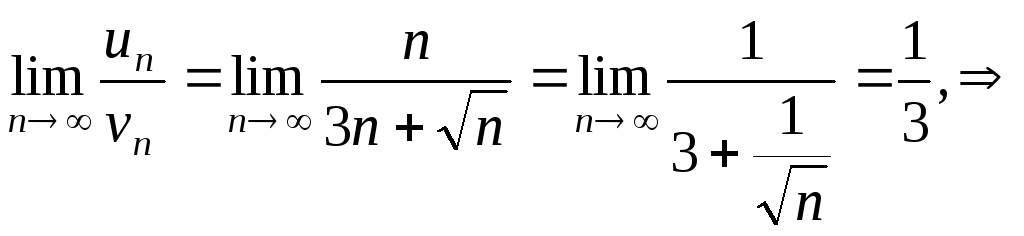ряд расходится по признаку сравнения, так как есть конечный предел, отличный от нуля.

17.31. Общий член ряда имеет вид .

_{Сравним ряд с гармоническим расходящимся рядом,}

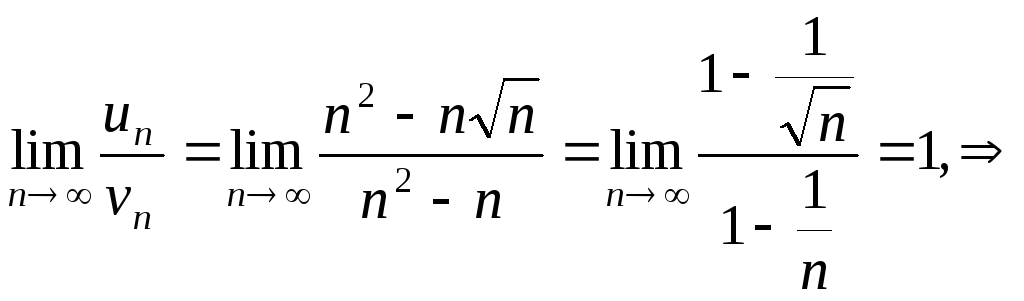ряд расходится по признаку сравнения, так как есть конечный предел, отличный от нуля.

17.32. Общий член ряда имеет вид .

_{Сравним ряд с гармоническим расходящимся рядом,}

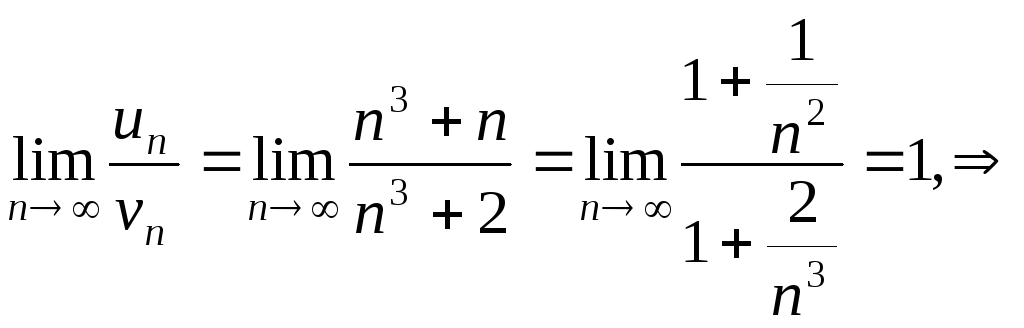ряд расходится по признаку сравнения, так как есть конечный предел, отличный от нуля.

Задачи 17.33-17.38: Исследовать сходимость ряда с помощью признака Даламбера:

17.33. Общий член ряда имеет вид .

Исследуем ряд по признаку Даламбера:

ряд сходится.

17.34. Общий член ряда имеет вид .

Исследуем ряд по признаку Даламбера:

ряд расходится.

17.35. Общий член ряда имеет вид .

Исследуем ряд по признаку Даламбера:

ряд сходится.

17.36. Общий член ряда имеет вид .

Исследуем ряд по признаку Даламбера:

ряд расходится.

17.37. Общий член ряда имеет вид .

Исследуем ряд по признаку Даламбера:

ряд сходится.

17.38. Общий член ряда имеет вид .

Исследуем ряд по признаку Даламбера:

ряд расходится.

Задачи 17.39-17.44: Исследовать по признаку Коши сходимость ряда:

17.39. Общий член ряда имеет вид .

Применим признак Коши:

_{Теперь найдем предел последней дроби:}

_{заданный ряд сходится.}

17.40. Общий член ряда имеет вид .

Применим признак Коши:

_{Теперь найдем предел последней дроби:}

_{заданный ряд расходится.}

17.41. Общий член ряда имеет вид .

Применим признак Коши:

_{Теперь найдем предел последней дроби:}

_{заданный ряд сходится.}

17.42. Общий член ряда имеет вид .

Применим признак Коши:

_{Теперь найдем предел последней дроби:}

_{заданный ряд сходится.}

17.43. Общий член ряда имеет вид .

Применим признак Коши:

_{Теперь найдем предел последней дроби:}

_{заданный ряд расходится.}

17.44. Общий член ряда имеет вид .

Применим признак Коши:

_{Теперь найдем предел последней дроби:}

_{заданный ряд сходится.}

Задачи 15.65-15.109: Найти интегралы, применив подходящие подстановки:

15.65.

15.66.

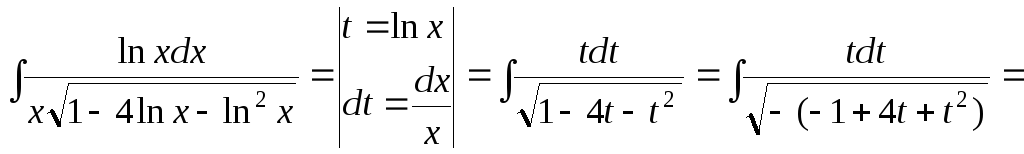
15.67.

15.68.

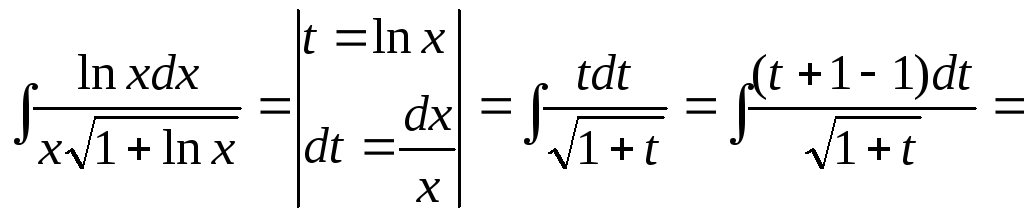
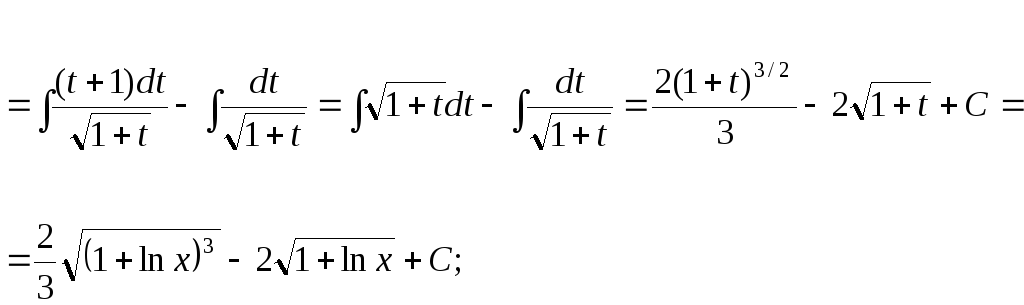
15.69.

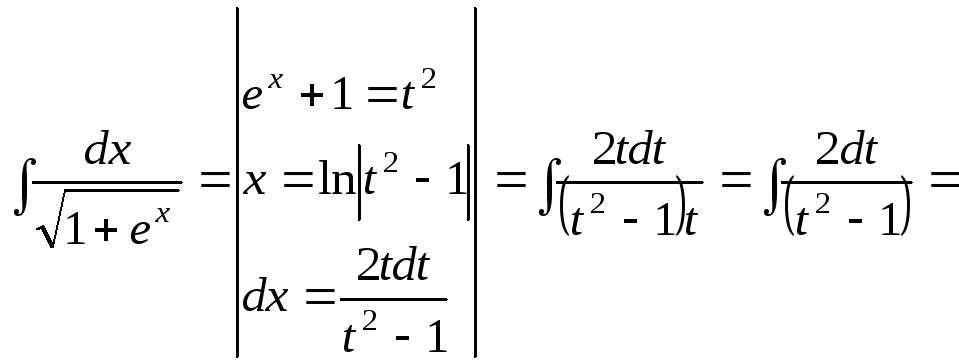
15.70.

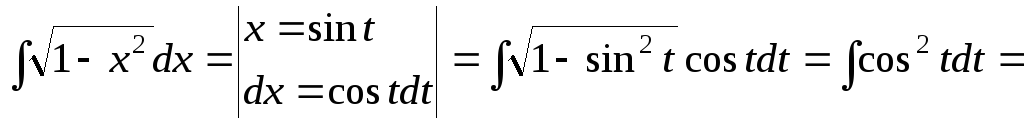
15.71

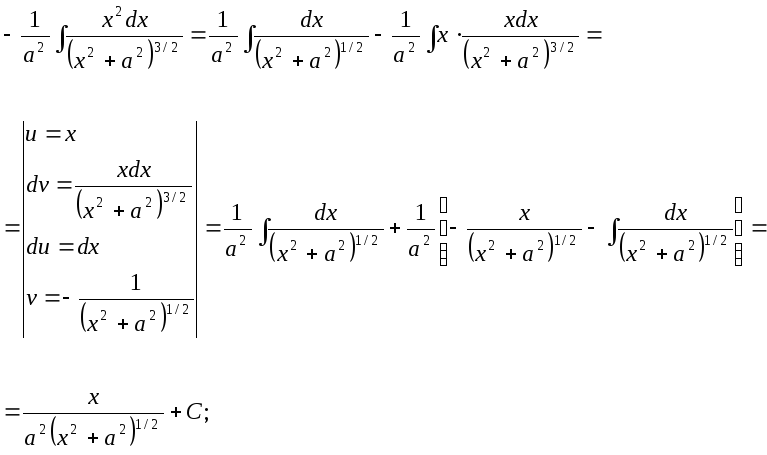
15.72.

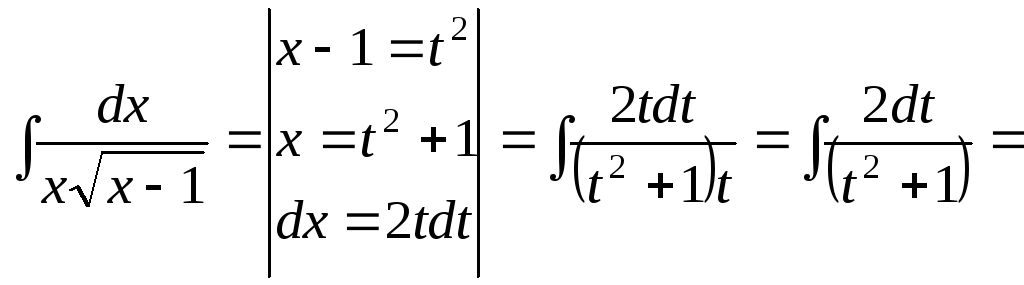
15.73.

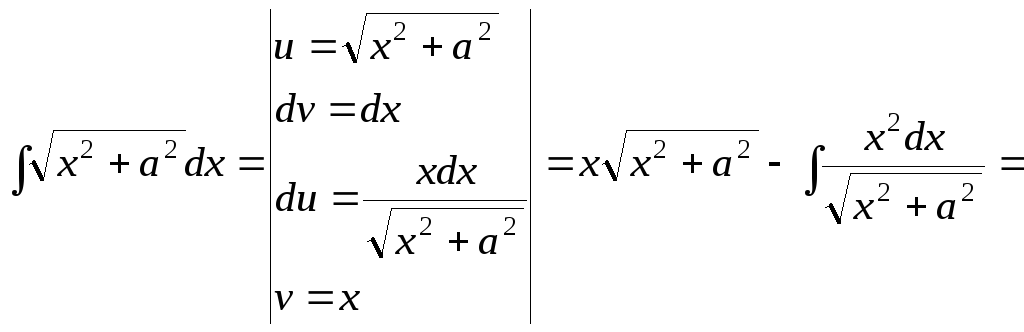
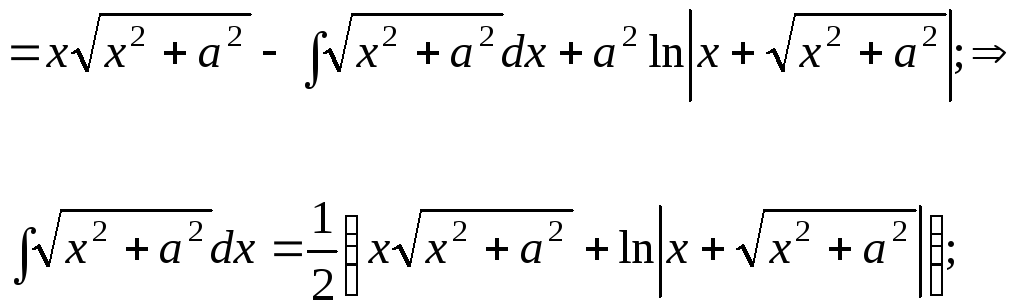
15.74.

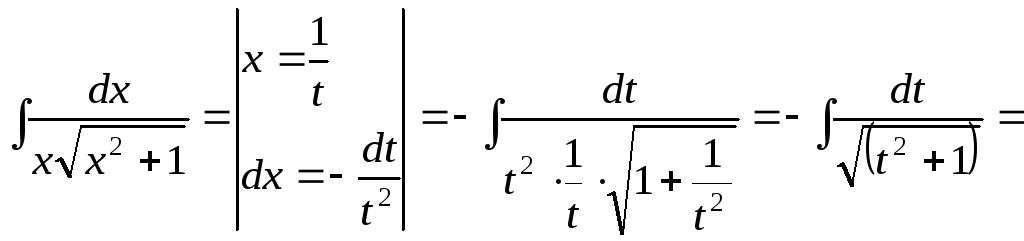
15.75.

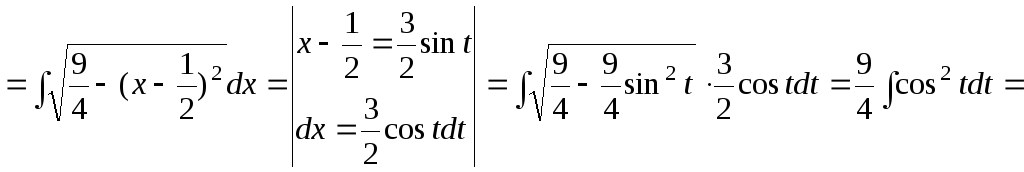
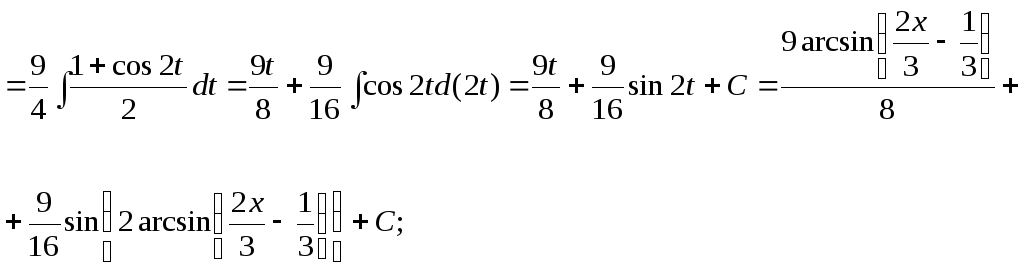
15.76.

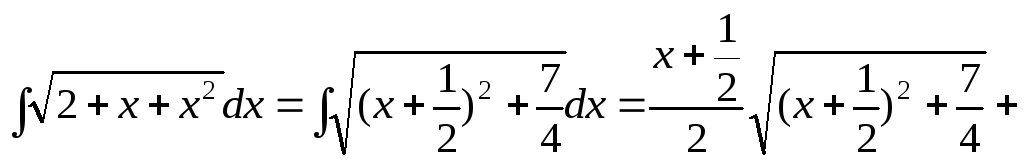
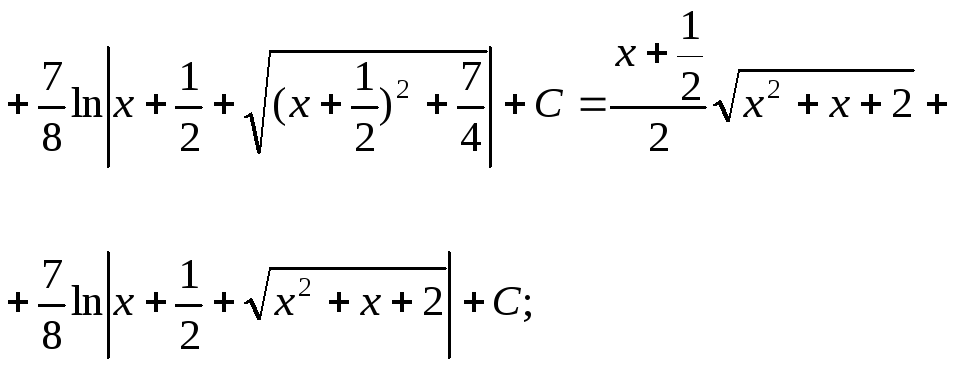
15.77.

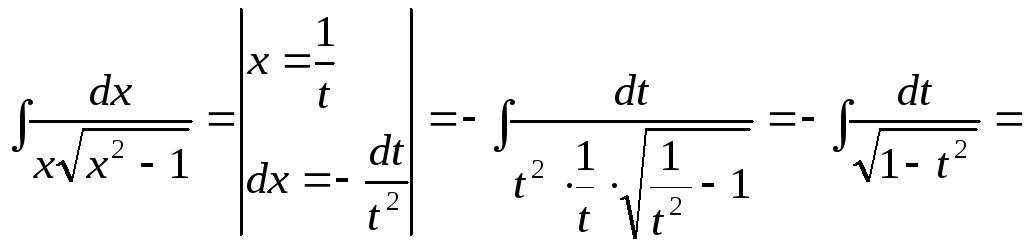
15.78.

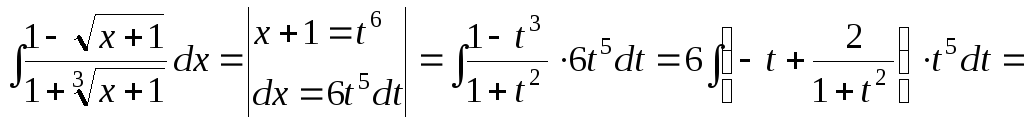
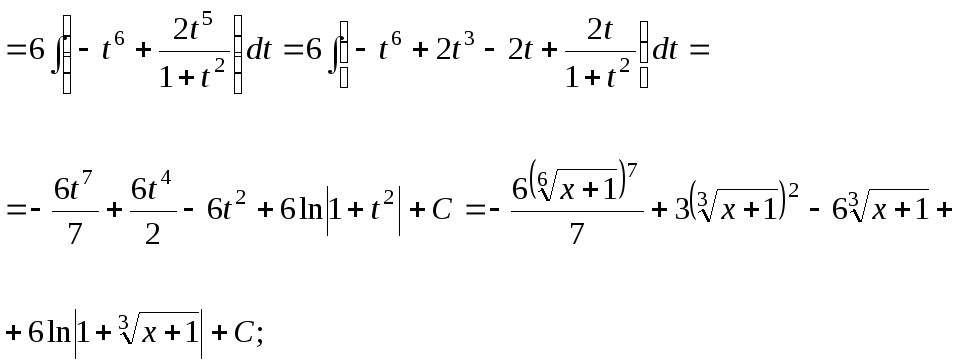
15.79.

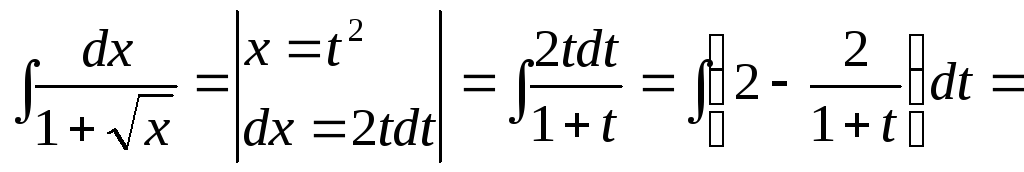
15.80.

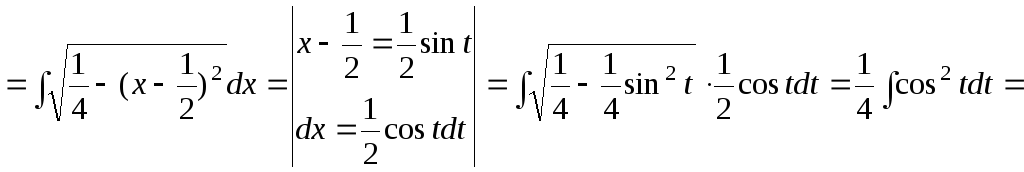
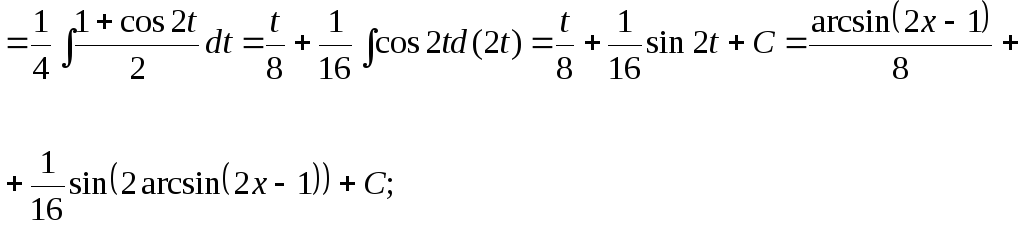
15.81.

15.82.

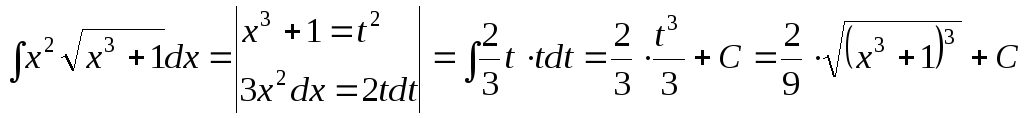
15.83.

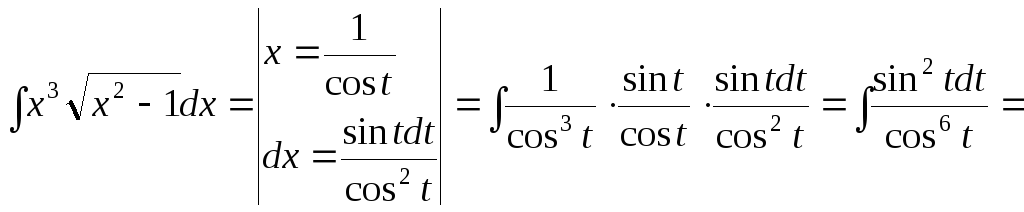
15.84.

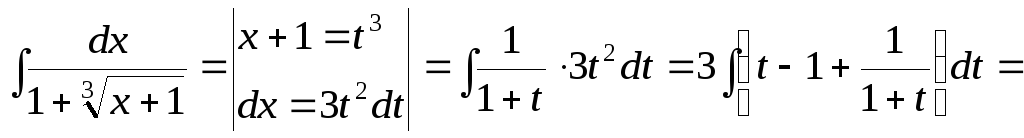
15.85.

15.86.

15.87.

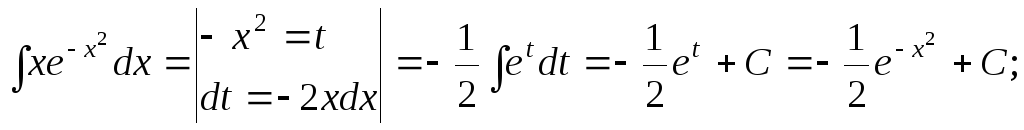
15.88.

15.89.

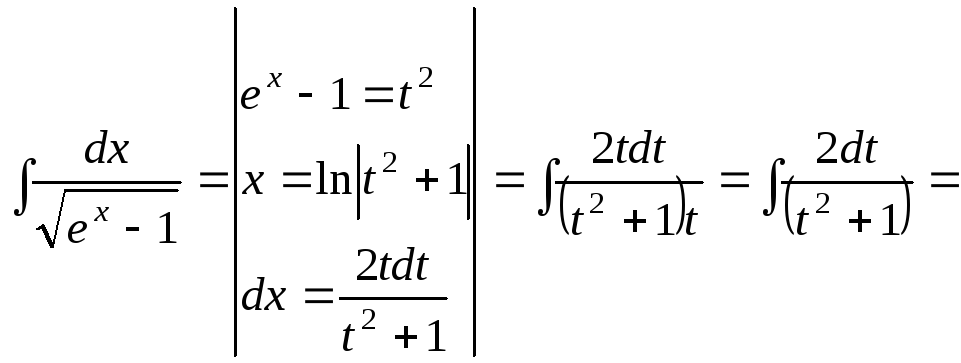
15.90.

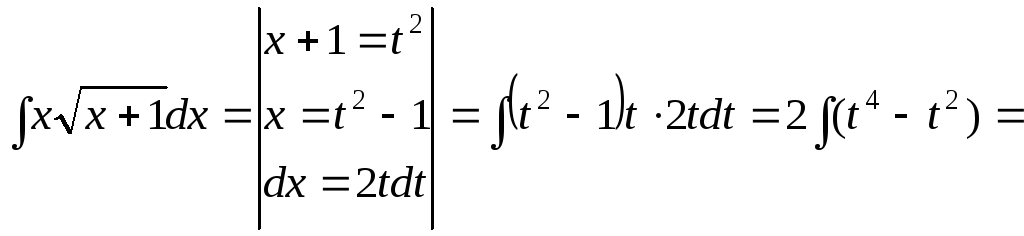
15.91.

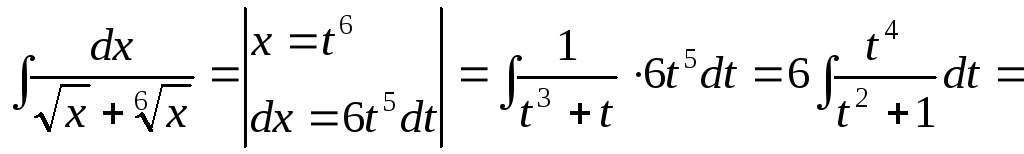
15.92.

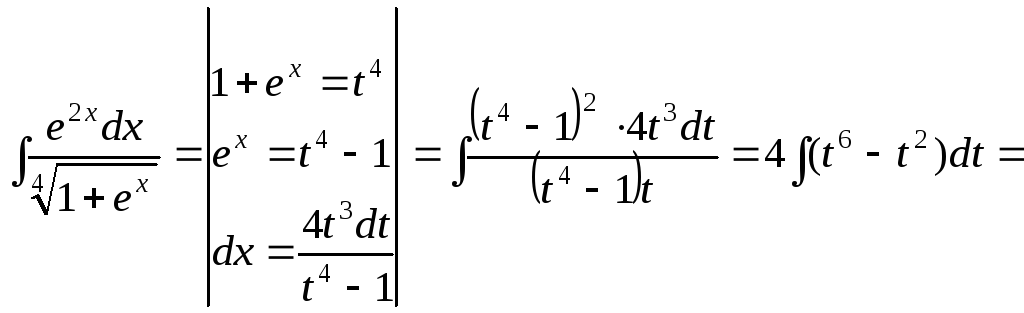
15.93.

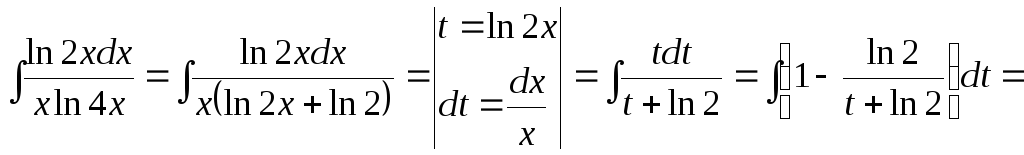
15.94.

15.95.

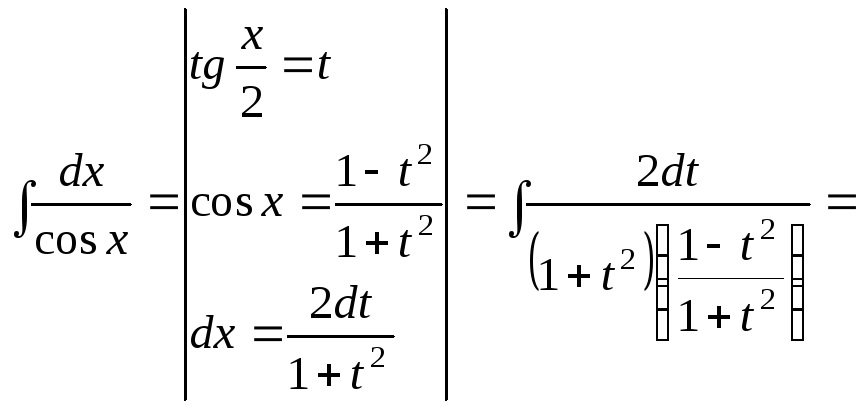
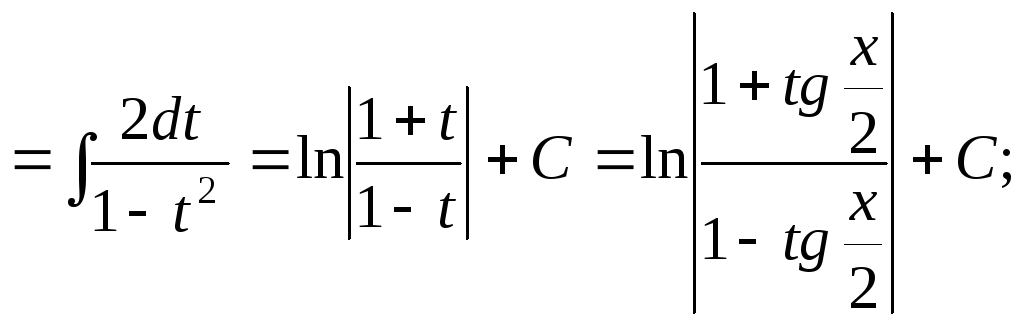
15.96.

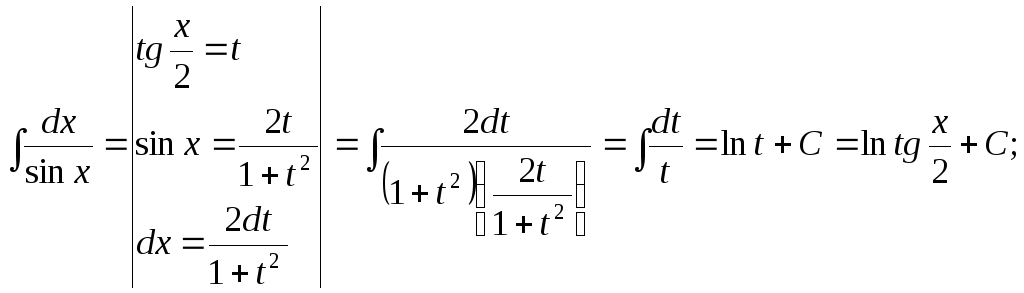
15.97.

15.98.

15.99.

15.100.

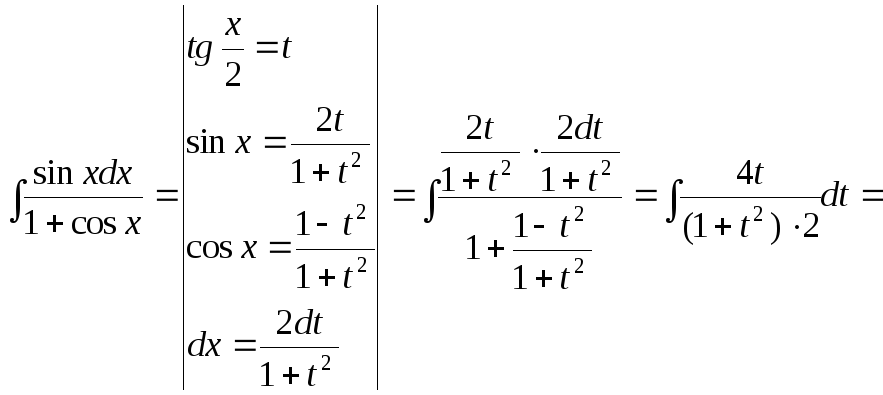
15.101.

15.102.

15.103.

15.104.

15.105.

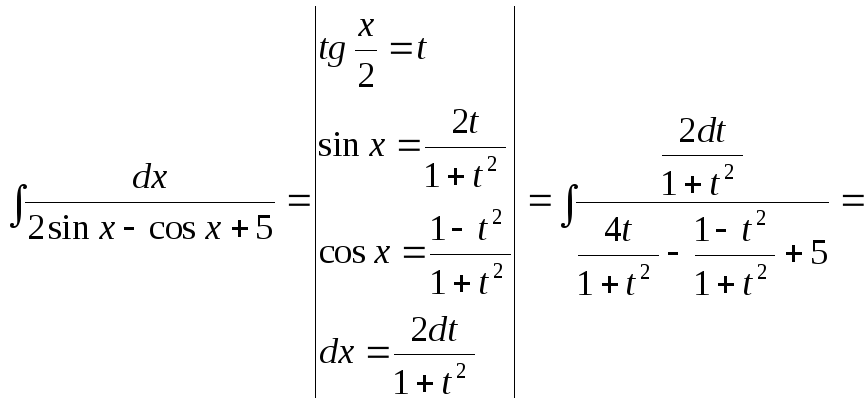
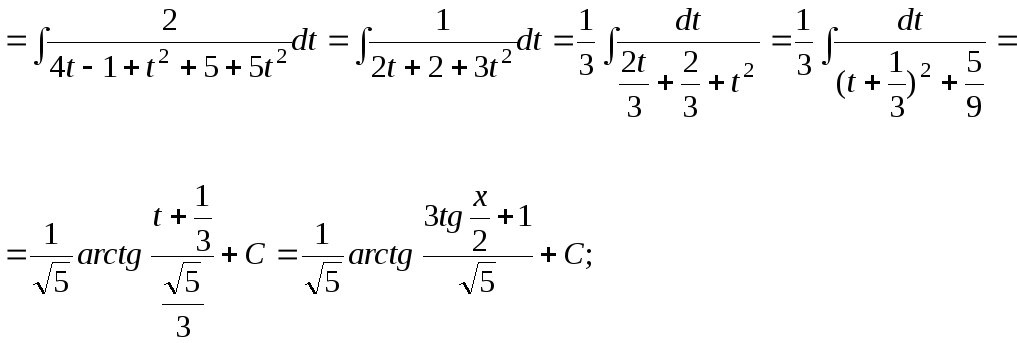
15.106.

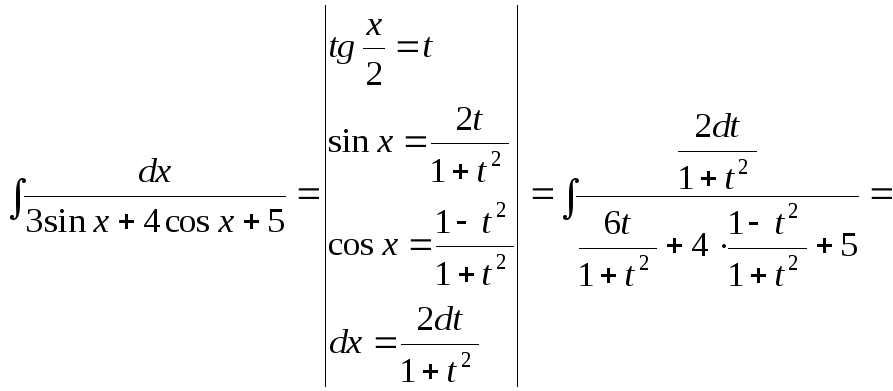
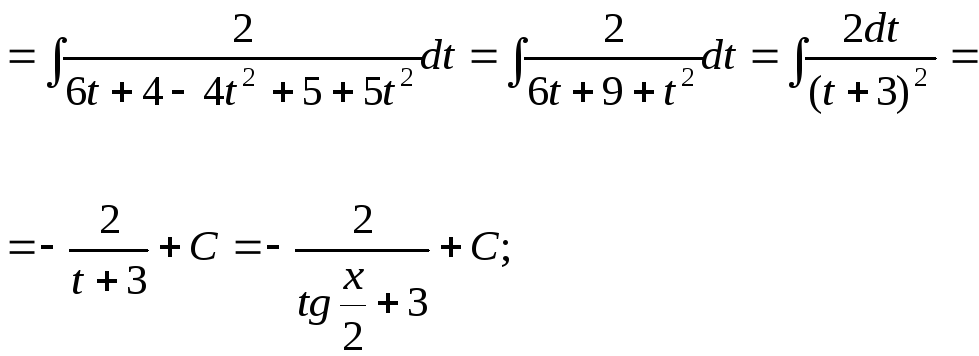
15.107.

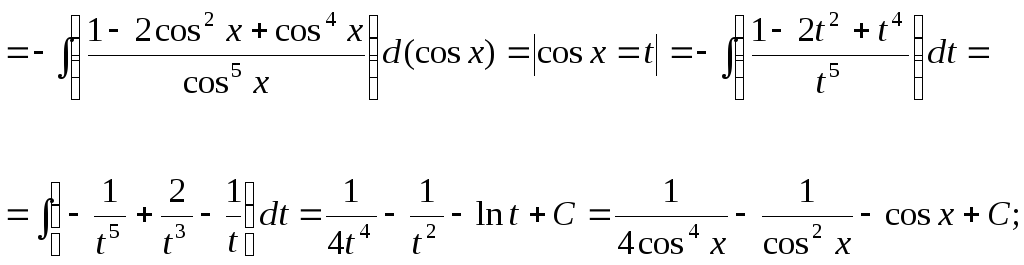
15.108.

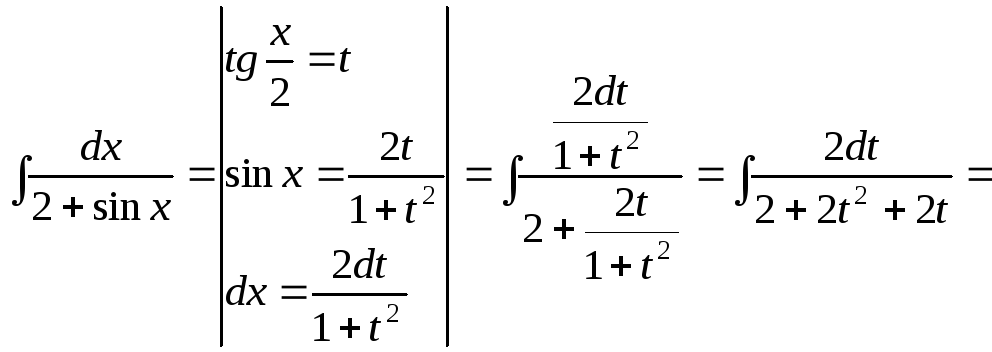
15.109.

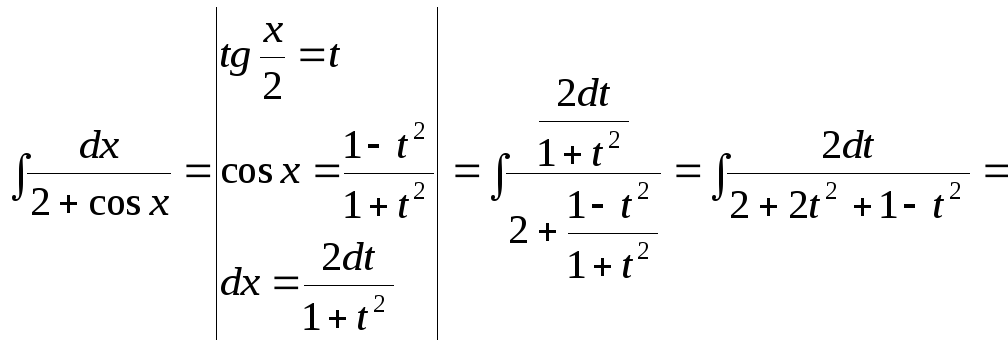
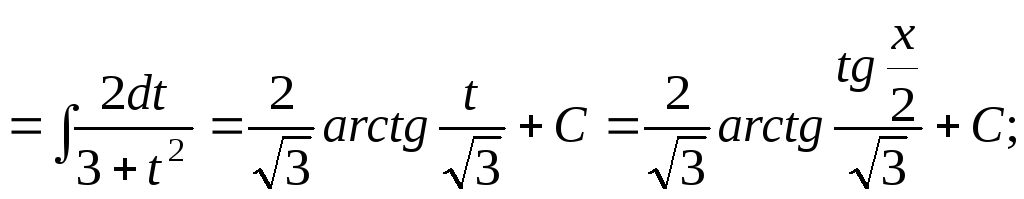
Задачи 15.110-15.129: Найти интегралы, применив метод интегрирования по частям:

15.110.

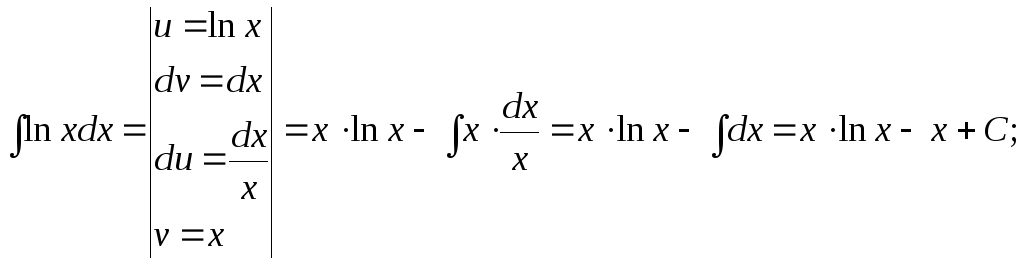
15.111.

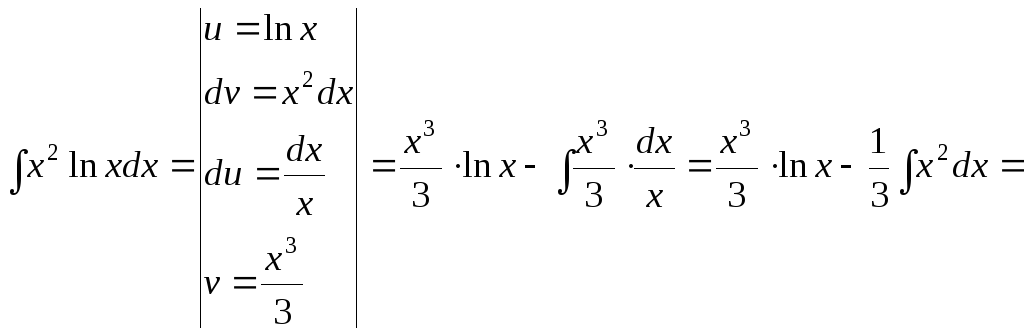
15.112.

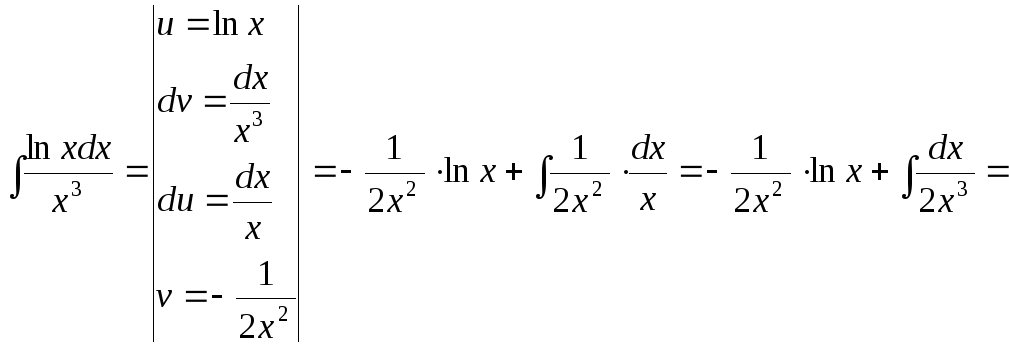
15.113.

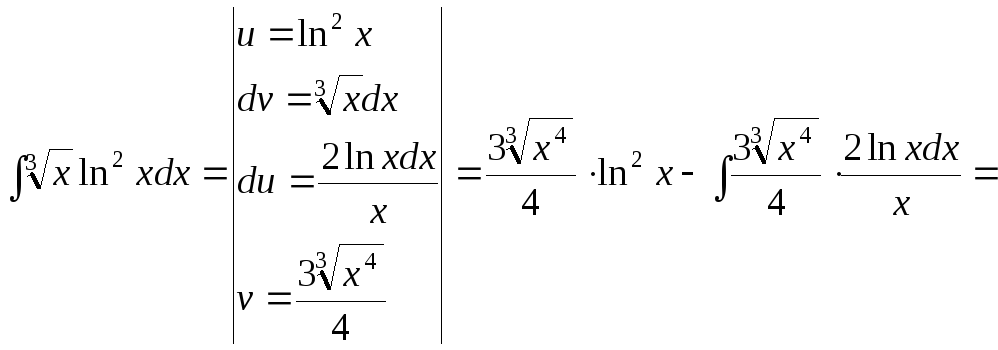
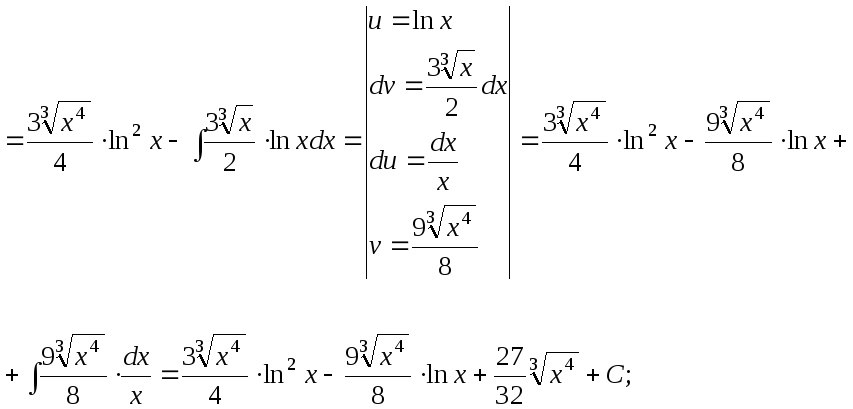
15.114.

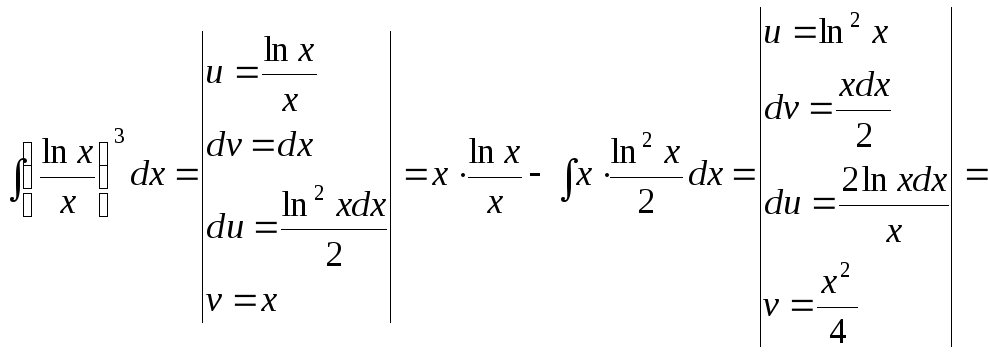
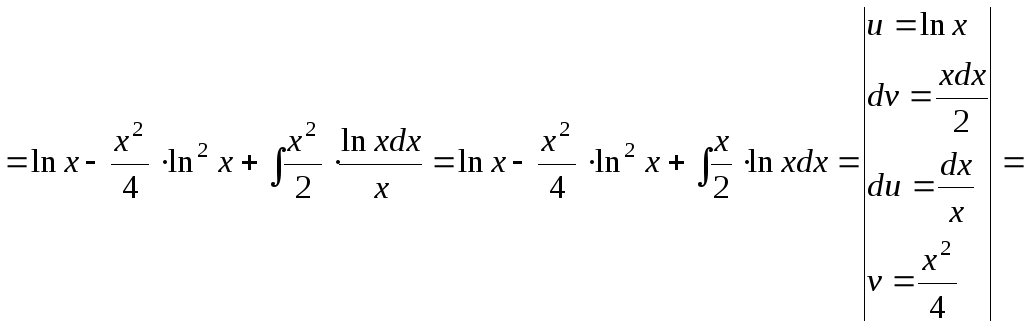
15.115.

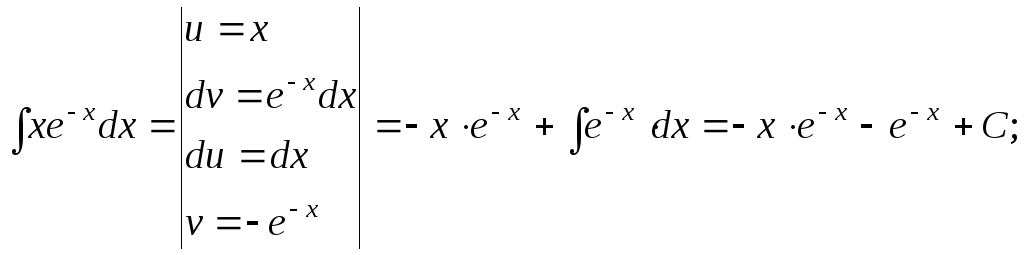
15.116.

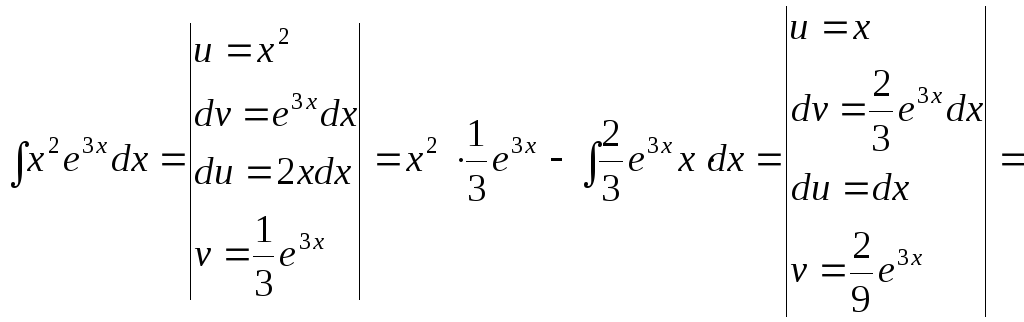
15.117.

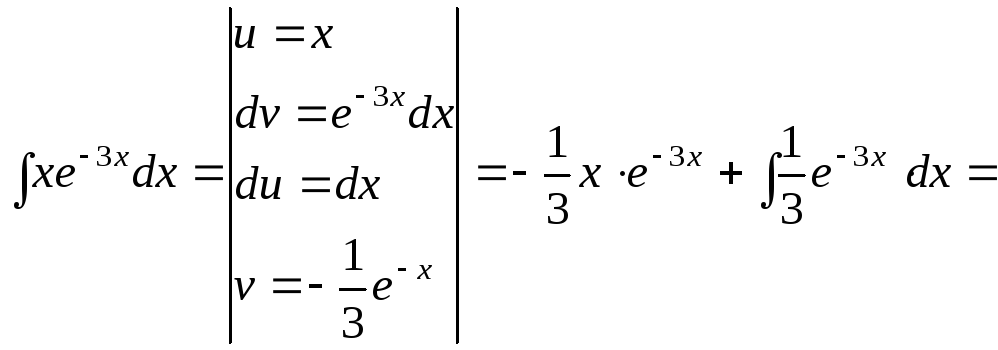
15.118.

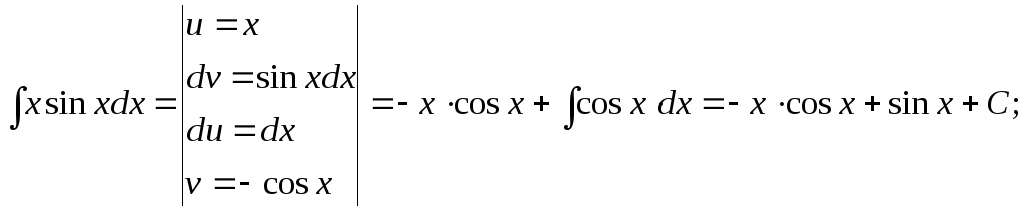
15.119.

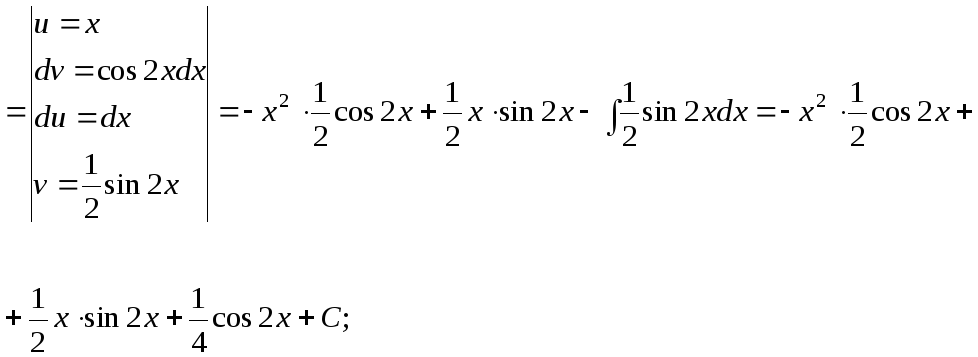
15.120.

15.121.

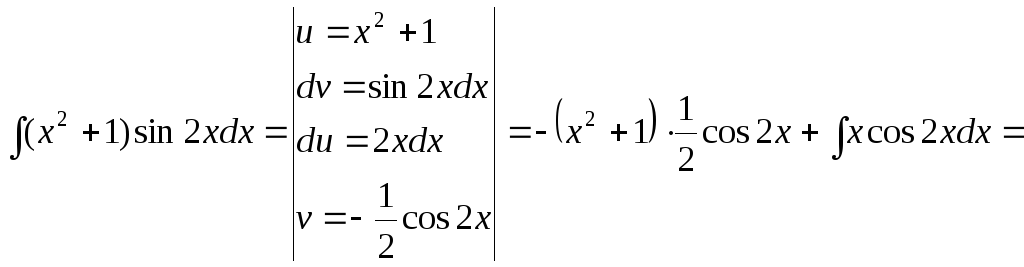
15.122.

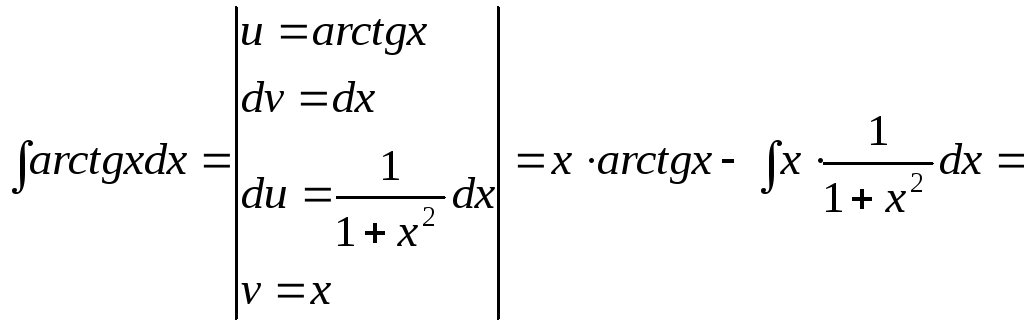
15.123.

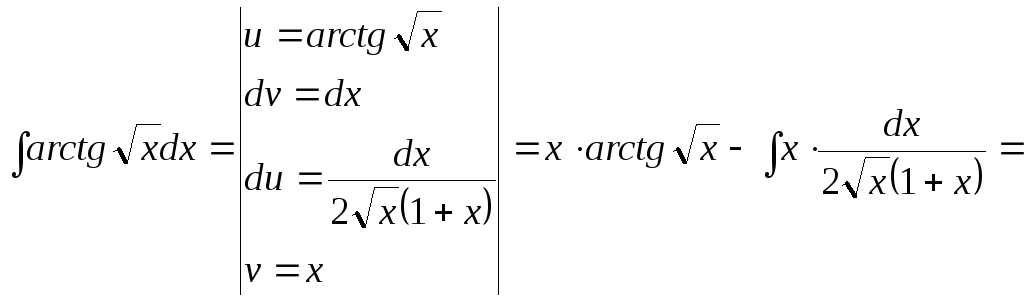
15.124.

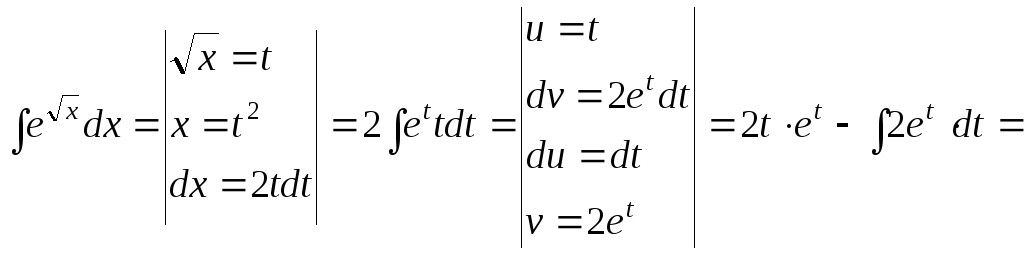
15.125.

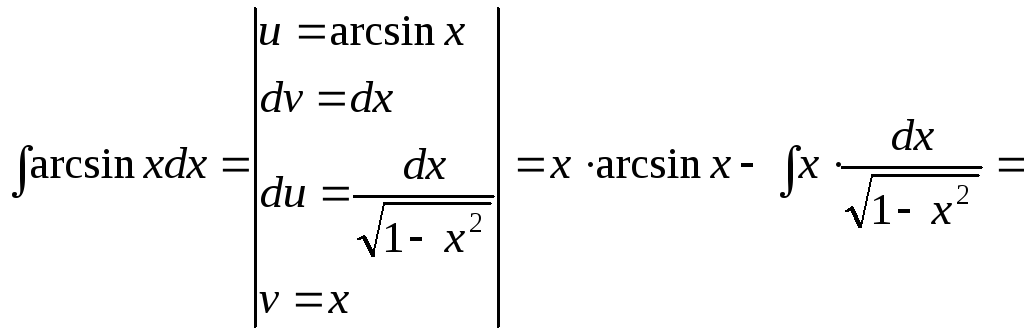
15.126.

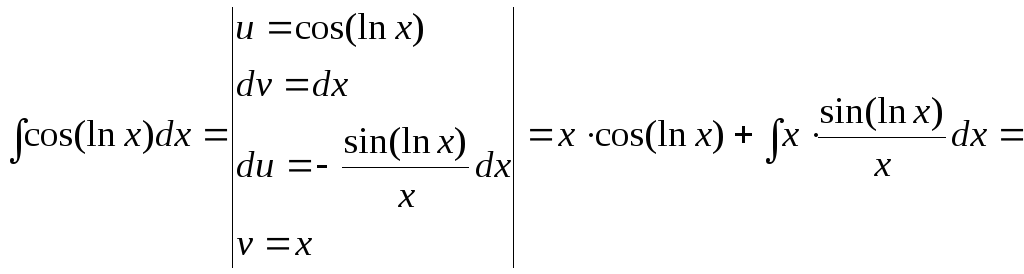
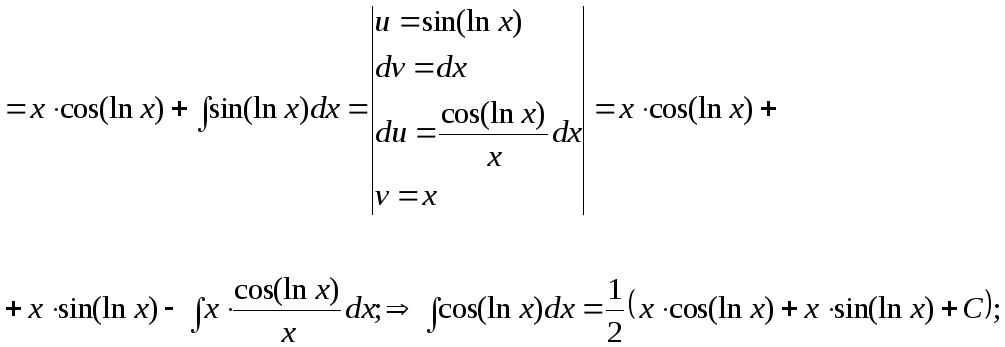
15.127.

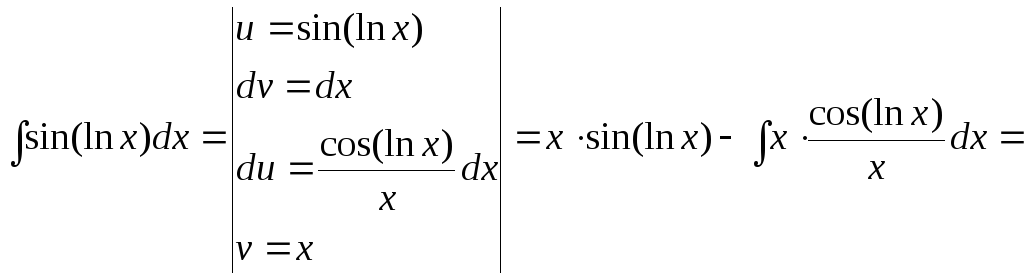
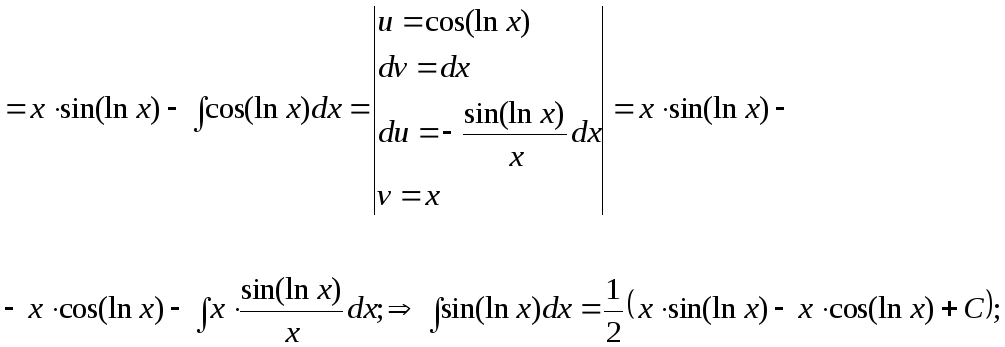
15.128.

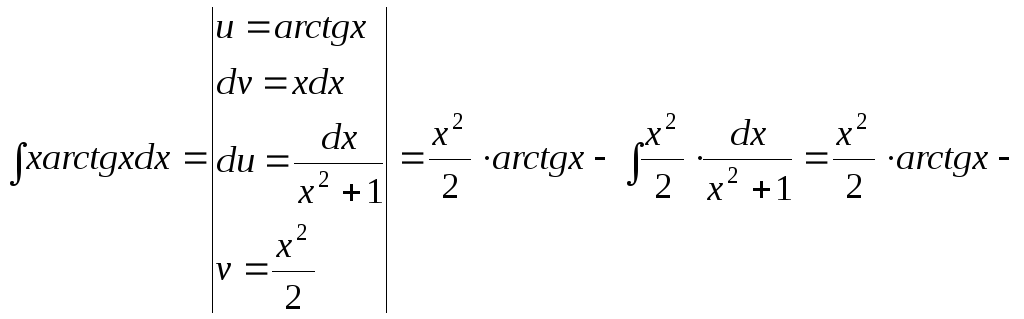
15.129.

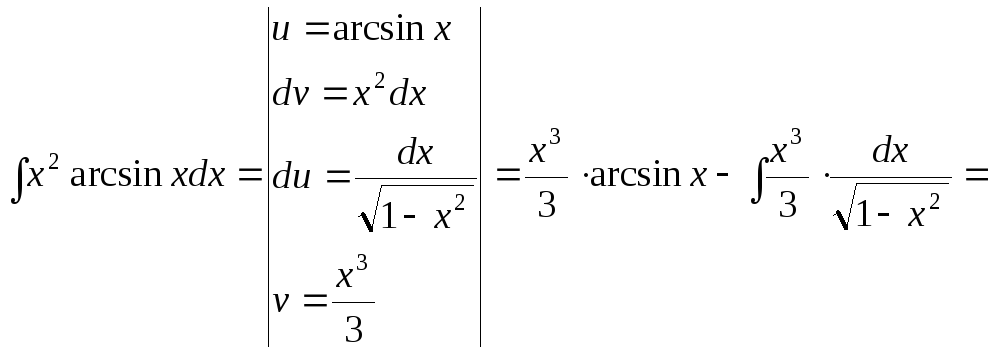
Задачи 17.13-17.18: Найти сумму ряда:

17.13. Общий член ряда имеет вид .

_{Найдем сумму ряда.}

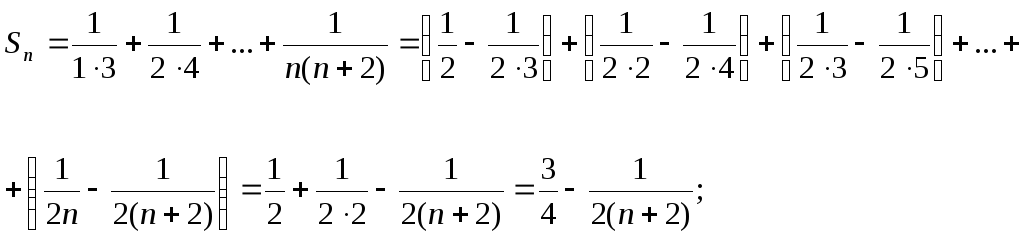
Поскольку

_{сумма ряда равна 3/4.}

17.14. Общий член ряда имеет вид .

_{Найдем сумму ряда.}

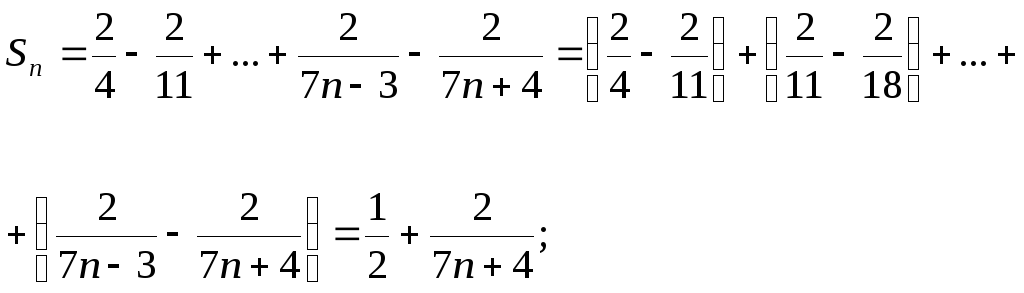
Поскольку

_{сумма ряда равна 1/2.}

17.15.Общий член ряда имеет вид .

_{Найдем сумму ряда.}

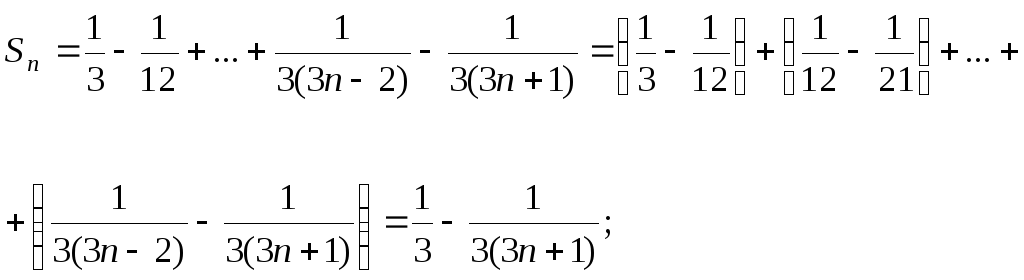
Поскольку

_{сумма ряда равна 1/3.}

17.16. Общий член ряда имеет вид .

_{Найдем сумму ряда.}

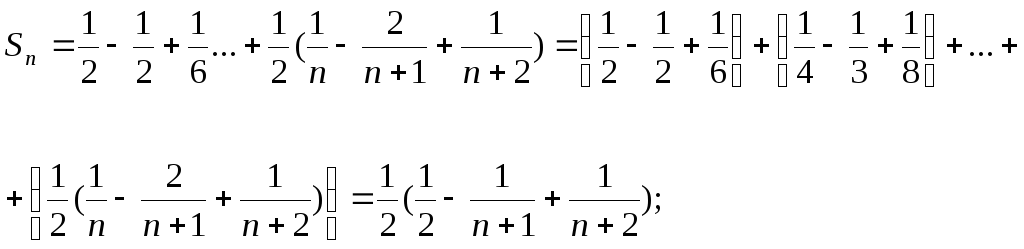
Поскольку

_{сумма ряда равна 1/4.}

17.17. Общий член ряда имеет вид .

_{Найдем сумму ряда.}

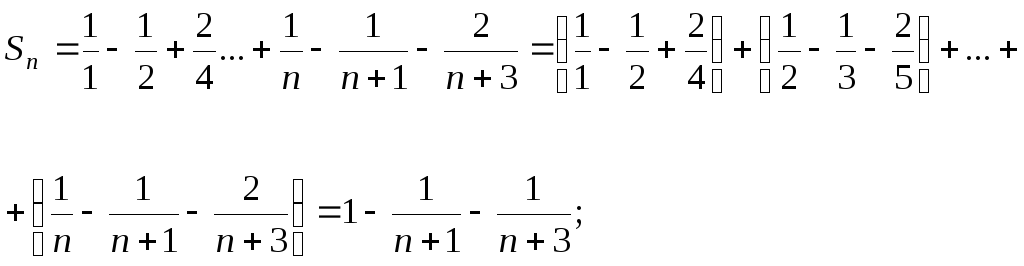
Поскольку

_{сумма ряда равна 1.}

17.18. Общий член ряда имеет вид .

_{Найдем сумму ряда.}

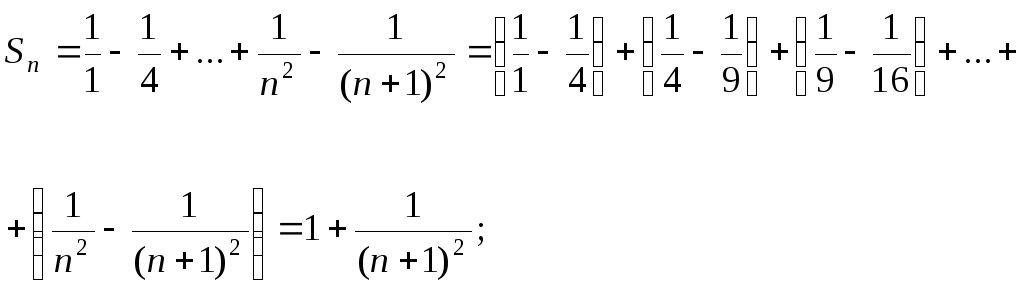
Поскольку

_{сумма ряда равна 1.}

Задачи 17.19-17.24: Исследовать сходимость ряда, используя следствие из необходимого признака сходимости:

17.19. Общий член ряда имеет вид . Данный числовой ряд расходится, так как не выполняется необходимый признак сходимости

ряд расходится.

17.20. Общий член ряда имеет вид . Данный числовой ряд расходится, так как не выполняется необходимый признак сходимости

ряд расходится.

17.21. Общий член ряда имеет вид . Данный числовой ряд сходится, так как выполняется необходимый признак сходимости

ряд сходится.

17.22. Общий член ряда имеет вид . Данный числовой ряд расходится, так как не выполняется необходимый признак сходимости

ряд расходится.

17.23. Общий член ряда имеет вид . Данный числовой ряд расходится, так как не выполняется необходимый признак сходимости

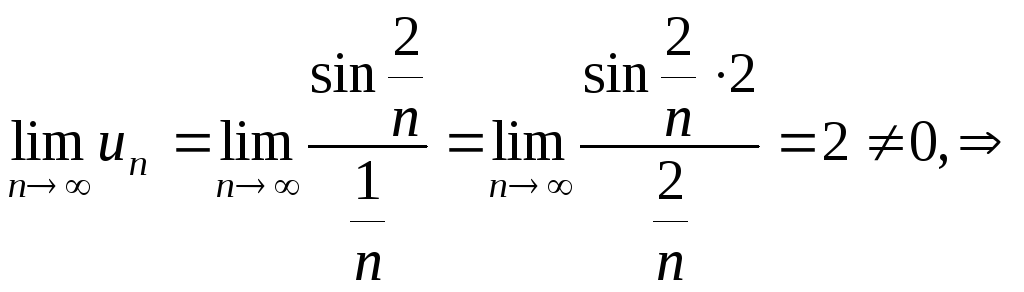ряд расходится.

17.24. Общий член ряда имеет вид . Данный числовой ряд расходится, так как не выполняется необходимый признак сходимости

ряд расходится.

Задачи 15.1-15.28: Найти интегралы:

15.1.

15.2.

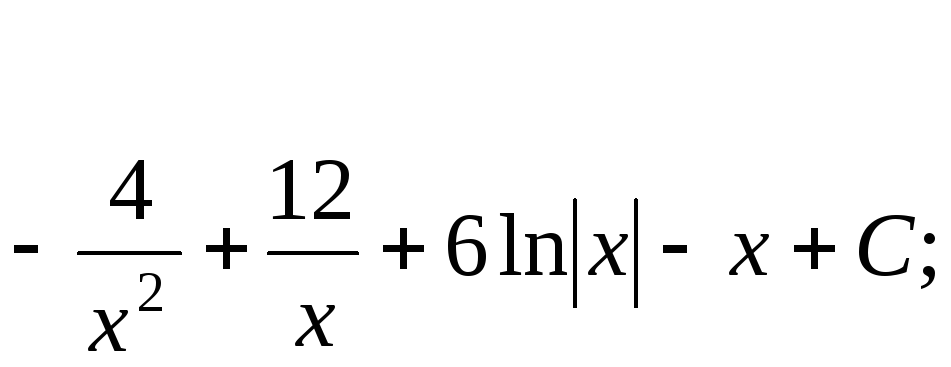
15.3.

15.4.

15.5.

15.6.

15.7

15.8.

15.9.

15.10.

15.11.

15.12.

15.13.

15.14.

15.15.

15.16.

15.17.

15.18.

15.19.

15.20.

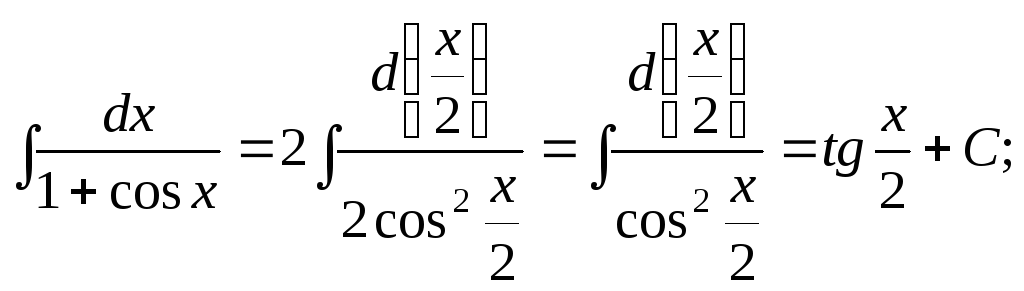
15.21.

15.22.

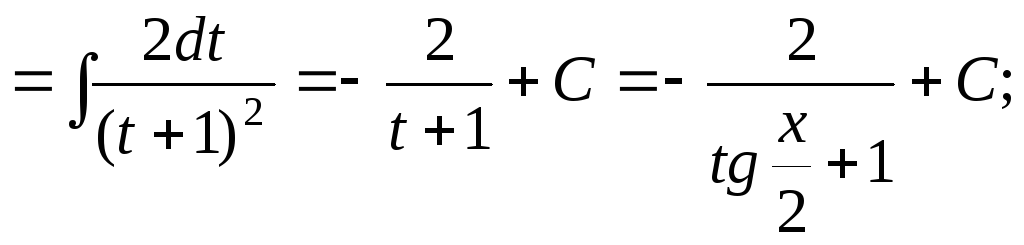
15.23.

15.24.

15.25.

15.26.

15.27.

15.28.

Задачи 16.9-16.29: Проинтегрировать уравнения, в отмеченных случаях найти частное решение:

16.9. - имеем дифференциальное уравнение с разделяющимися переменными. Решим его:

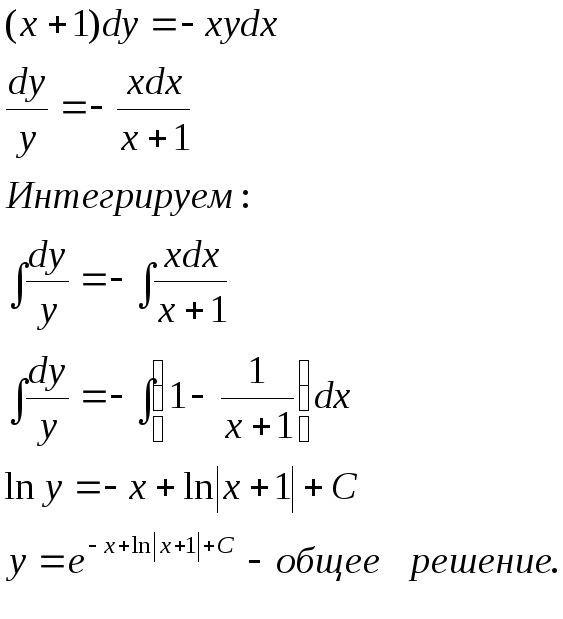
16.10. - имеем дифференциальное уравнение с разделяющимися переменными. Решим его:

16.11. - имеем дифференциальное уравнение с разделяющимися переменными. Решим его:

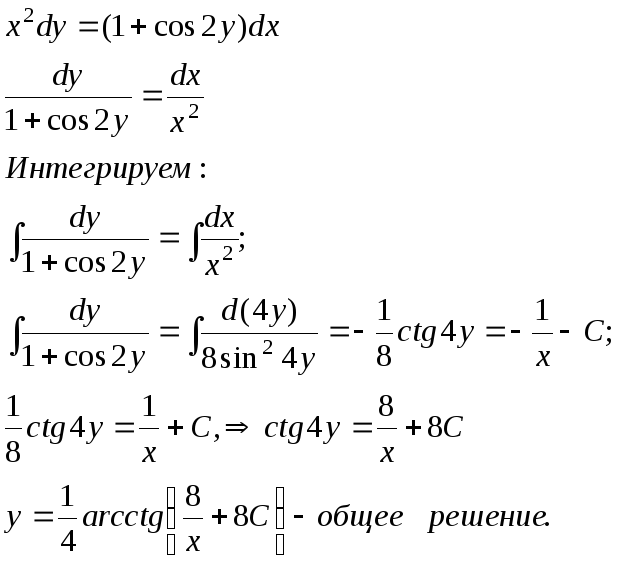
16.12. - имеем дифференциальное уравнение с разделяющимися переменными. Решим его:

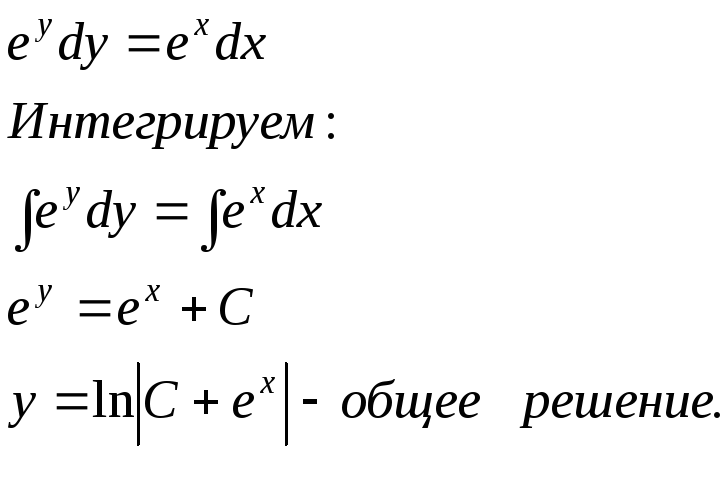
16.13. - имеем дифференциальное уравнение с разделяющимися переменными. Решим его:

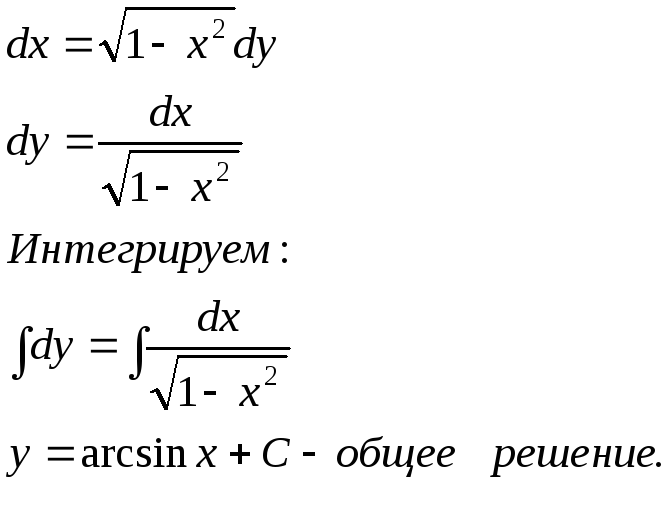
16.14. - имеем дифференциальное уравнение с разделяющимися переменными. Решим его:

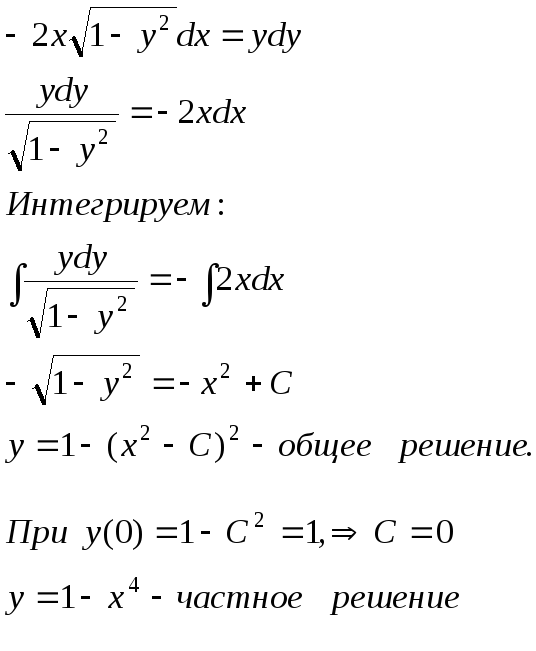
16.15. - имеем дифференциальное уравнение с разделяющимися переменными. Решим его:

16.16. - имеем дифференциальное уравнение с разделяющимися переменными. Решим его:

16.17. - имеем дифференциальное уравнение с разделяющимися переменными. Решим его:

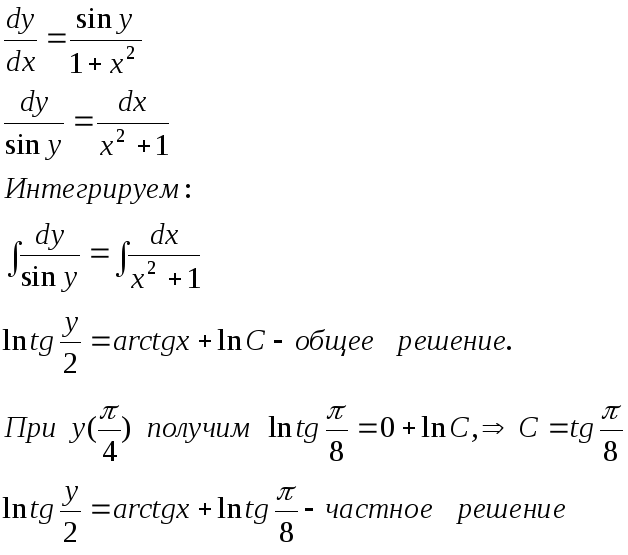
16.18. - имеем дифференциальное уравнение с разделяющимися переменными. Решим его:

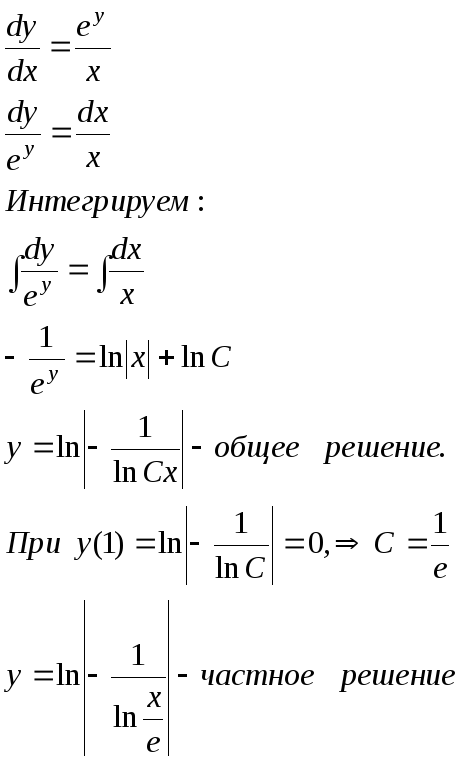
16.19. - имеем дифференциальное уравнение с разделяющимися переменными. Решим его: