
- •1. Основні властивості неперервних функцій
- •1. Поняття рівномірної неперервності функції.
- •2. Теорема Кантора про рівномірну неперервність функції.
- •3. Теорема про неперервність оберненої функції.
- •Тема 5. Диференціальне числення функції однієї змінної
- •1. Задачі, що проводять до поняття похідної
- •Після спрощення одержуємо
- •2. Означення похідної
- •3. Механічний та геометричний зміст похідної
- •4. Односторонні похідні
- •5. Нескінченні похідні
- •1. Диференційовність функції
- •2. Похідні елементарних функцій
- •3. Похідна оберненої функції.
- •1. Диференціал функції
- •2. Похідні й диференціали вищих порядків
- •3. Формула Лейбніца для п-ної похідної добутку двох функцій.
- •4. Диференціали вищих порядків.
- •Тема 5. Застосування диференціального числення до дослідження функцій
- •1. Теореми про середнє значення
- •2. Теорема Ферма
- •3. Теорема Ролля
- •4. Теорема Лагранжа
- •5. Теорема Коші
- •1. Розкриття невизначеностей. Правило Лопіталя.
- •2. Застосування правила Лопіталя при розкритті невизначеностей вигляду .
- •1. Формула Тейлора для многочлена. Розглянемо многочлен
- •6.2. Формула Тейлора для довільної функції
- •Звідси одержуємо:
- •1. Ознака монотонності функції
- •3. Необхідні й достатні умови існування екстремуми функції
- •Достатні умови існування екстремуму функції.
- •1. Опуклість та вгнутість кривої. Точки перегину
- •2. Асимптоти графіка функції
- •3. Загальна схема дослідження функцій і побудови їх графіків
- •Тема 7. Інтеграл ньютоналейбніца
- •1. Поняття первісної функції та невизначеного інтеграла
- •2. Основні властивості невизначеного інтеграла
- •3. Таблиця основних інтегралів
- •1. Подання раціональних дробів у вигляді суми найпростіших дробів
- •2. Інтегрування найпростіших раціональних дробів
- •1. Інтегрування ірраціональних функцій
- •Інтегрування деяких тригонометричних функцій
- •Приклади
ЛЕКЦІЯ 13
Основні властивості неперервних функцій.
1. Основні властивості неперервних функцій
Перша теорема Больцано-Коші (теорема
про обернення функції в нуль).Нехай
функція![]() неперервна на відрізку
неперервна на відрізку![]() і на його кінцях значення функції мають
різні знаки. Тоді існує точка
і на його кінцях значення функції мають
різні знаки. Тоді існує точка![]() така, що
така, що![]() .
.
Доведення.Нехай для визначеності![]() .
Розділимо відрізок
.
Розділимо відрізок![]() навпіл. Якщо
навпіл. Якщо ,
то теорема доведена. Якщо
,
то теорема доведена. Якщо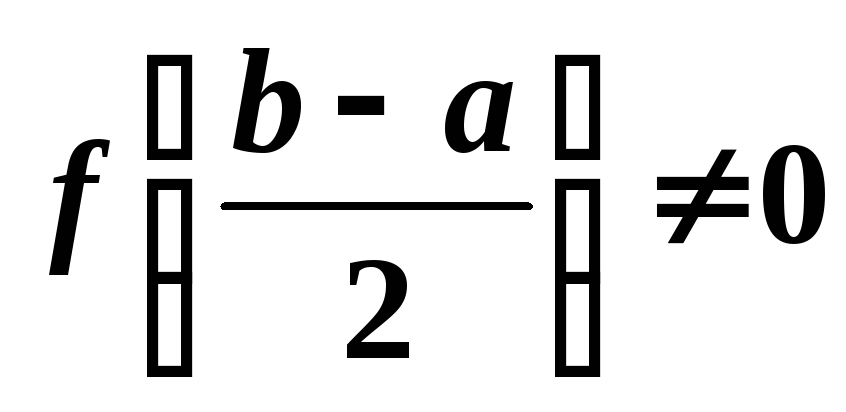 ,
то виберемо ту половину відрізка
,
то виберемо ту половину відрізка![]() ,
на кінцях якої функція
,
на кінцях якої функція![]() має значення різних знаків, і позначимо
її
має значення різних знаків, і позначимо
її![]() .
Розділимо відрізок
.
Розділимо відрізок![]() навпіл. Якщо
навпіл. Якщо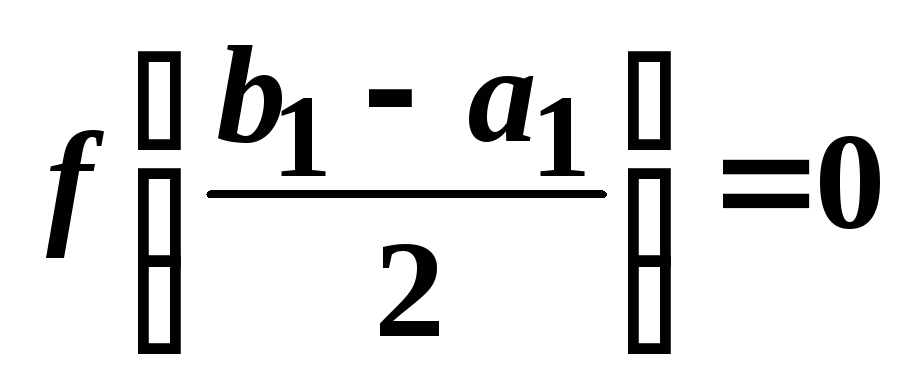 ,
то теорема доведена, в іншому випадку
виберемо ту половину відрізка
,
то теорема доведена, в іншому випадку
виберемо ту половину відрізка![]() ,
на кінцях якої функція
,
на кінцях якої функція![]() має значення різних знаків, та позначимо
її
має значення різних знаків, та позначимо
її![]() .
Якщо цей процес продовжувати необмежено,
то або на якомусь
.
Якщо цей процес продовжувати необмежено,
то або на якомусь![]() -ому
кроці значення функції в середині
відрізка
-ому
кроці значення функції в середині
відрізка![]() буде рівним нулю і тоді теорема доведена,
або одержимо послідовність укладених
відрізків
буде рівним нулю і тоді теорема доведена,
або одержимо послідовність укладених
відрізків
![]()
таких, що
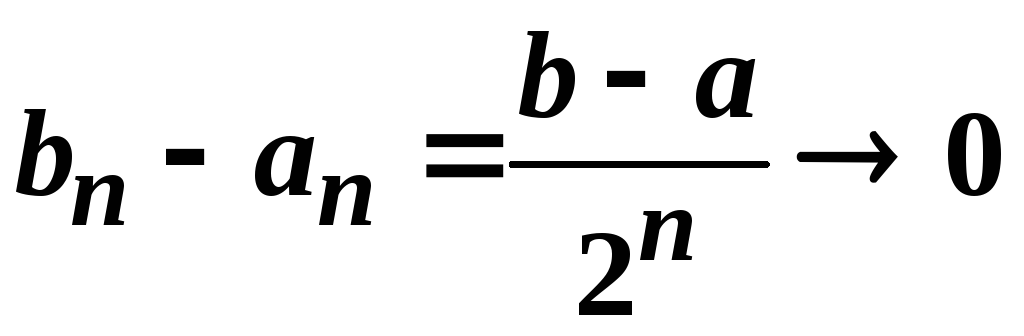 при
при![]() і на кінцях кожного з відрізків
і на кінцях кожного з відрізків![]() функція
функція![]() має значення різних знаків,
має значення різних знаків,![]() .
.
За теоремою
про вкладені відрізки існує точка
![]() ,
яка належить кожному із відрізків
,
яка належить кожному із відрізків![]() і
і![]()
![]() .
Ураховуючи неперервність функції
.
Ураховуючи неперервність функції![]() (зокрема в точці
(зокрема в точці![]() ),
маємо
),
маємо![]() .
.
Звідси
одержуємо
![]() .
.
Друга
теорема Больцано-Коші (теорема про
проміжне значення).Нехай функція![]() неперервна на відрізку
неперервна на відрізку![]() і на кінцях цього відрізка приймає
значення
і на кінцях цього відрізка приймає
значення![]() де
де![]() .
Тоді для будь-якого числа
.
Тоді для будь-якого числа![]() існує точка
існує точка![]() така, що
така, що![]() .
.
Доведення.Нехай для визначеності![]() .
Розглянемо допоміжну функцію
.
Розглянемо допоміжну функцію
![]() .
Ця функція неперервна на відрізку
.
Ця функція неперервна на відрізку![]() і
і
![]() ,
,![]() .
.
За першою
теоремою Больцано-Коші існує точка
![]() така, що
така, що![]() .
Але
.
Але![]() .
Отже,
.
Отже,![]() ,
тобто
,
тобто![]() .
.
Перша
теорема Вейєрштрасса.Якщо функція![]() неперервна на відрізку
неперервна на відрізку![]() ,
то вона обмежена на цьому відрізку.
,
то вона обмежена на цьому відрізку.
Доведення.Нехай функція![]() неперервна на відрізку
неперервна на відрізку![]() .
Припустимо, що вона на відрізку
.
Припустимо, що вона на відрізку![]() не обмежена. Поділимо відрізок
не обмежена. Поділимо відрізок![]() пополам і виберемо ту його частину, де
функція
пополам і виберемо ту його частину, де
функція![]() не обмежена. Позначимо її
не обмежена. Позначимо її![]() .
Відрізок
.
Відрізок![]() також поділимо пополам і виберемо ту
його частину, де функція
також поділимо пополам і виберемо ту
його частину, де функція![]() не обмежена. Позначимо вибрану половину
не обмежена. Позначимо вибрану половину![]() .
Продовжуючи необмежено цей процес,
одержимо послідовність укладених
відрізків
.
Продовжуючи необмежено цей процес,
одержимо послідовність укладених
відрізків
![]()
таких, що
 при
при![]() .
За теоремою про вкладені відрізки існує
точка
.
За теоремою про вкладені відрізки існує
точка![]() ,
яка належить кожному із них і
,
яка належить кожному із них і![]() .
За означенням границі послідовності
для будь-якого числа
.
За означенням границі послідовності
для будь-якого числа![]() >0
існує такий номер
>0
існує такий номер![]() ,
що при
,
що при![]() з іншого боку, існує такий номер
з іншого боку, існує такий номер![]() ,
що при
,
що при![]() .
Нехай
.
Нехай![]() .
Тоді при
.
Тоді при![]() виконуються нерівності:
виконуються нерівності:![]() , тобто всі відрізки
, тобто всі відрізки![]() ,
де
,
де![]() попадають в інтервал
попадають в інтервал![]() .
Таким чином, функція
.
Таким чином, функція![]() не обмежена в деякому
не обмежена в деякому![]() -околі
точки
-околі
точки![]() .
Але це неможливо, оскільки функція
.
Але це неможливо, оскільки функція![]() неперервна на відрізку
неперервна на відрізку![]() ,
а значить, неперервна і в точці
,
а значить, неперервна і в точці![]() ,
тобто в точці
,
тобто в точці![]() існує скінченна границя функції
існує скінченна границя функції![]() ,
а тому в околі цієї точки вона обмежена.
,
а тому в околі цієї точки вона обмежена.
Друга
теорема Вейєрштрасса.Якщо функція![]() неперервна на відрізку
неперервна на відрізку![]() ,
то вона досягає на цьому відрізку своїх
точних меж, тобто існують такі точки
,
то вона досягає на цьому відрізку своїх
точних меж, тобто існують такі точки![]() ,
що
,
що
![]() .
.
Доведення.Нехай функція![]() неперервна на відрізку
неперервна на відрізку![]() .
За першою теоремою Вейєрштрасса функція
.
За першою теоремою Вейєрштрасса функція![]() на відрізку
на відрізку![]() обмежена. Отже, вона має точну верхню
межу
обмежена. Отже, вона має точну верхню
межу
![]() і точну нижню межу
і точну нижню межу
![]() .
Покажемо, що існує точка
.
Покажемо, що існує точка![]() така, що
така, що![]() .
Припустимо, що в жодній точці відрізка
.
Припустимо, що в жодній точці відрізка![]() функція
функція![]() не приймає значення, рівного
не приймає значення, рівного![]() ,
тобто для всіх точок
,
тобто для всіх точок![]() .
Складемо допоміжну функцію
.
Складемо допоміжну функцію .
Ця функція на відрізку
.
Ця функція на відрізку![]() неперервна, а тому обмежена. Отже, існує
число
неперервна, а тому обмежена. Отже, існує
число![]() таке, що для всіх
таке, що для всіх![]()
 .
.
Із цієї
нерівності маємо:
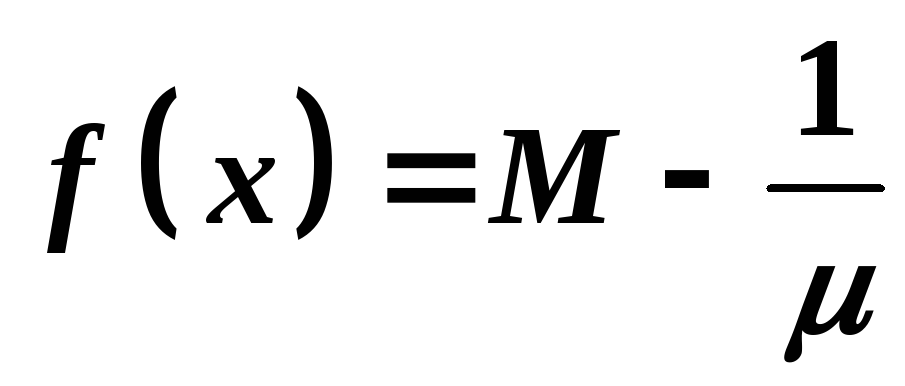 .
Таким чином,
.
Таким чином, – верхня межа функції
– верхня межа функції![]() на відрізку
на відрізку![]() .
Але це суперечить тому, що число
.
Але це суперечить тому, що число![]() точна верхня межа цієї функції на
відрізку
точна верхня межа цієї функції на
відрізку![]() .
Звідси випливає, що зроблене припущення
неправильне, тобто існує точка
.
Звідси випливає, що зроблене припущення
неправильне, тобто існує точка![]() така, що
така, що![]() .
.
Друга частина теореми доводиться аналогічно.
Зауваження.Точна верхня межа функції![]() ,
неперервної на відрізку
,
неперервної на відрізку![]() ,
називається її найбільшим (максимальним)
значенням на цьому відрізку, а точна
нижня межа – її найменшим (мінімальним)
значенням. Різниця
,
називається її найбільшим (максимальним)
значенням на цьому відрізку, а точна
нижня межа – її найменшим (мінімальним)
значенням. Різниця![]() ,
де
,
де
![]() ,
називається коливанням функції на
відрізку
,
називається коливанням функції на
відрізку![]() .
.
ЛЕКЦІЯ 14
Поняття рівномірної неперервності функції.
Теорема Кантора про рівномірну неперервність функції.
Теорема про неперервність оберненої функції.
