Властивості:

1. .

Дійсно, (x, y) = (x, y) = (x, y) = (x, y).

2. .

Дійсно, (Ax, y) = (x, A*y) = (A*y, x) = (y, (A*)^* x) = ((A*)^* x, y).

3. .

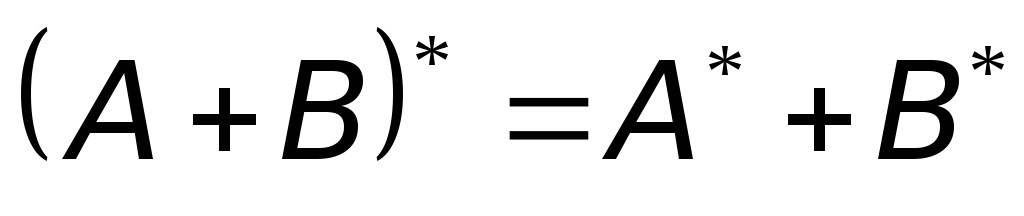Дійсно, (x, (A + B)*y) = ((A + B)x, y) = (Ax + Bx, y) = (Ax, y) + (Bx, y) =

= (x, A*y) + (x, B*y) = (x, (A^* + B*)y).

4.

Дійсно, (x, (AB)*y) = ((AB)x, y) = (A (Bx), y) = (Bx, A*y) = (x, B^*(A*)y) = (x, (B ^*A*)y).

5. Якщо 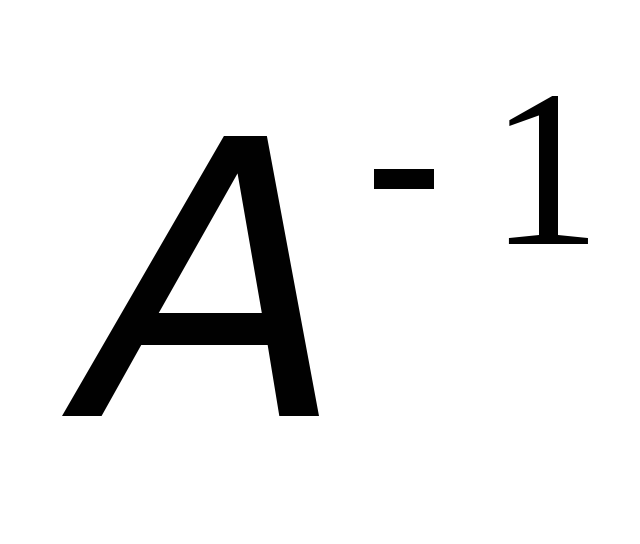існує, то.

Дійсно, .

б) Самоспряжені перетворення

Самоспряженим (симетричним) називається перетворення, яке співпадає із своїм спряженим, тобто .

Якщо A – самоспряжене перетворення, то x, y V (Ax, y)=( x, Ay).

Якщо матрицею самоспряженого перетворення A в ортонормованому базисі є A=[a_ij], тоді A' = A, тобто a_ij = a_ji. Така матриця називається симетричною.

Властивості:

1. Тотожнє перетворення є самоспряженим, оскільки .

2. Сума самоспряжених перетворень є самоспряженим перетворенням.

.

3. Перетворення, обернене до невиродженого самоспряженого перетворення, є самоспряженим перетворенням.

.

4. Добуток самоспряжених перетворень є самоспряженим перетворенням тоді і тільки тоді, коли ці перетворення переставні між собою.

а) якщо ,і, то, тобто.

б) якщо ,і, то, тобто– самоспряжене перетворення.

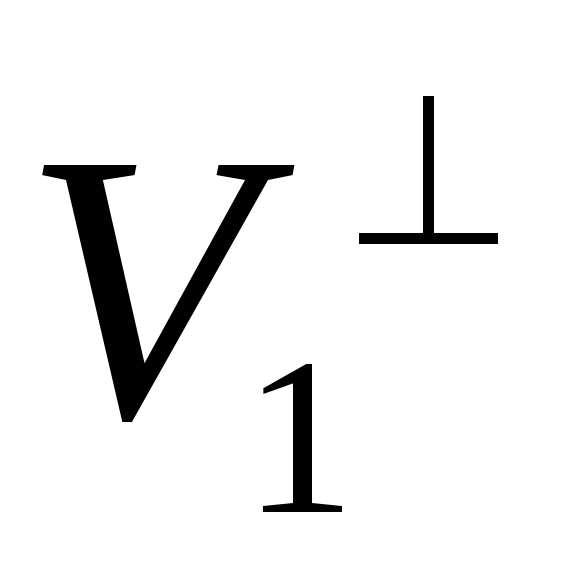5. Якщо підпростір інваріантний відносно лінійного перетворенняA, то його ортогональне доповнення інваріантне відносно спряженого доA перетворення .

Нехай х – довільний вектор із ,у – довільний вектор із . Тоді (A^*x, y) = = (x, Ay) = 0, оскільки Ay і, значить,хAy. Значить, вектор A^*x, іє інваріантним відносно.

Наслідок. Якщо A – самоспряжене перетворення і підпростір, інваріантний відносноA, то і інваріантний відносноA.

6. Всі корені характеристичного многочлена самоспряженого перетворення A дійсні (власні значення самоспряженого оператора дійсні).

(Ax, х) = (λx, х),

(x, Aх) = = (x, х).

Оскільки A – самоспряжений, то (Ax, х) = (x, Aх), значить , тобто– дійсне.

7. Власні вектори, що відповідають різним власним значенням самоспряженого оператора, ортогональні.

Нехай – власні значення самоспряженого оператора A, а х₁ та х₂ – відповідні їм власні вектори.

(Ax₁, х₂) = λ₁(x₁, х₂), (x₁, Aх₂) = λ₂ (x₁, х₂).

(Ax₁, х₂) = (x₁, Aх₂ ), бо A – самоспряжений. Тоді

(x₁, х₂) = 0 (x₁, х₂) = 0,

що й треба було довести.

8. Матриця самоспряженого оператора в деякому ортонормованому базисі зводиться до діагонального вигляду.

Нехай – одне із власних значень самоспряженого оператораA (дійсне).

Відповідний власний вектор позначимо е₁, тобто Aе₁ = λ₁е₁. Вектор е₁ можна вважати одиничним, оскільки інакше його можна замінити одиничним власним вектором з тим же власним значенням.

Позначимо через одновимірний підпростір, породжений вектором е₁. Його ортогональне доповнення буде інваріантним відносноA. Нехай – (дійсне) власне значення перетворенняA в підпросторі , відповідний (одиничний) власний вектор позначимо е₂. Тоді Aе₂ = λ₂е₂. Нехай буде (інваріантним) підпростором, породженим векторами е₁ і е₂. Тоді підпростір теж інваріантний відносноA. Продовжуючи цю побудову, ми знайдемо попарно ортогональних (значить, лінійно незалежних) одиничних власних векторів перетворенняA. В базисі, що складається із цих векторів, матриця А перетворення A зводиться до діагонального вигляду:

Aе₁ = λ₁е₁,

Aе₂ = λ₂е₂,

…………..

Aе_n = λ_nе_n,

звідки А = .

Геометрично самоспряжене лінійне перетворення зводиться до розтягів з коефіцієнтамивздовжкоординатних осей, співнапрямлених зе₁, е_2,, …, е_n відповідно.

в) Ортогональні перетворення

Лінійне перетворення Aевклідового просторуVназиваєтьсяортогональним, якщо воно зберігає скалярний добуток векторів, тобто якщоx, y V (Ax,Ay) = (x,y).

Це означає , що ортогональне перетворення зберігає довжини векторів та кути між ними (тому ортогональні перетворення іноді називають ізометричними).

Ясно, що ортогональне перетворення переводить довільний ортонормований базис в ортонормований і навпаки.