lekcii / lektion5

Лекція 5

Алгебра матриць

§1. Поняття матриці

Матрицею порядку mn називають таблицю елементів із m рядків і n стовпчиків. Позначають:

А=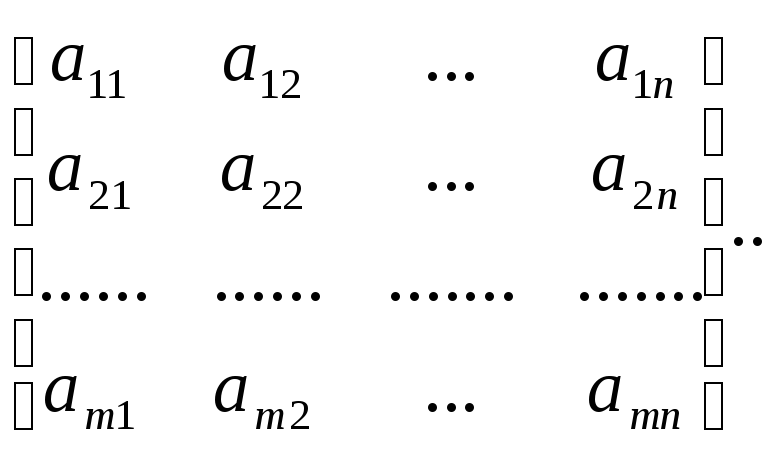=, де і=1,2,...,m, j=1,2,…,n,

або те саме в круглих дужках.

Матрицю порядку mn утворюють, наприклад, коефіцієнти при невідомих в системі m лінійних рівнянь з n невідомими:

Перші індекси біля елементів є номерами рядків, а другі - стовпчиків.

Елементи а_іі матриці A утворюють головну діагональ.

Дві матриці називають рівними, якщо співпадають їх елементи, що знаходяться на відповідних місцях. Матриця , утворена із матриці А, в якій рядки і стовпчики помінялись місцями , називається транспонованою до матриці А:

.

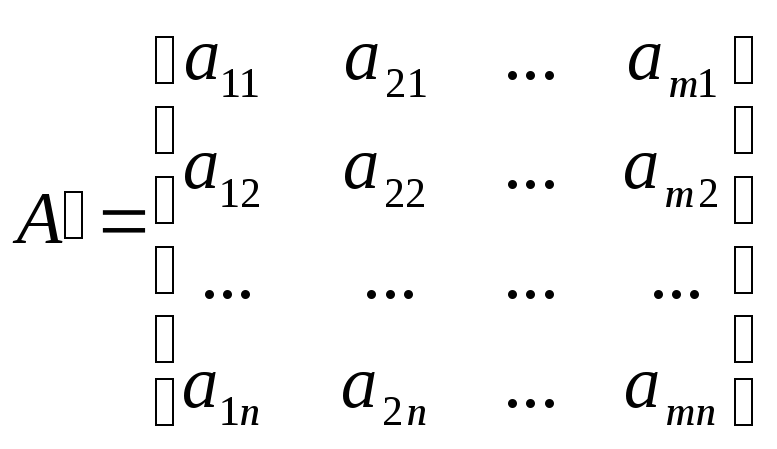Якщо всі елементи матриці рівні нулю, то матриця називається нульовою. Позначають θ.

Матрицю називають верхньою (нижньою) трикутною, якщо всі її елементи нижче (вище) головної діагоналі є рівними нулю.

Матрицю називають квадратною порядку n, якщо кількості рядків і стовпчиків співпадають і рівні n.

Квадратна матриця []порядку n називається симетричною, якщо

[a=a], і кососиметричною, якщо [= -], i j.

Матриця, у якої всі елементи, крім діагональних, рівні нулю, називається діагональною.

Якщо всі елементи діагональної матриці рівні між собою, то матрицю називають скалярною, якщо ж всі ці діагональні елементи рівні 1, то матрицю називають одиничною. Позначають Е.

Матрицю називають ступінчастою, якщо вона задовольняє такі умови:

1) якщо в і-му рядку перший ненульовий елемент знаходиться на k-му місці, то в

наступному і+1-му рядку на перших k місцях знаходяться нулі;

2) якщо кожен елемент і-того рядка рівний нулю, то й кожен елемент наступного

і+1-го рядка теж дорівнює нулю.

П

риклад.

,.

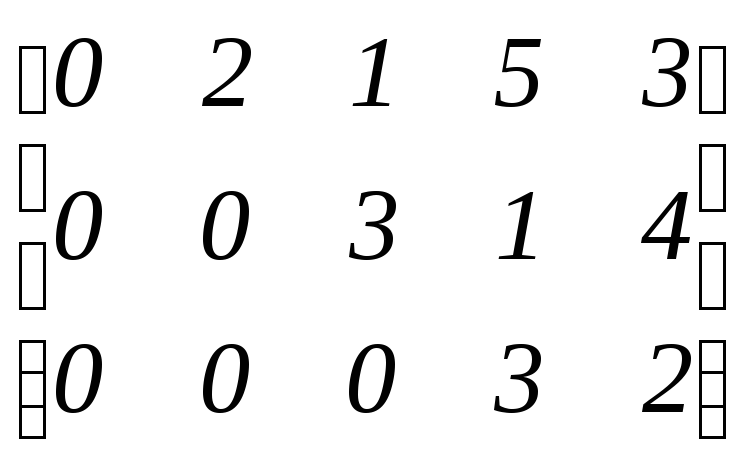Елементарними перетвореннями матриці А називають такі операції:

1. переставляння двох рядків (стовпчиків) матриці А;

2. множення рядка (стовпчика) матриці А на деяке відмінне від нуля число с;

3. додавання до одного рядка (стовпчика) матриці А іншого її рядка (стовпчика), помноженого на деяке число с.

§2.Дії над матрицями

Нехай А=і В= - довільно вибраніпрямокутні(m, n) - матриці.

Сумою матриць А та В називають матрицю S =, де

,

Записують S=A+B.

Додавання матриць зводиться до додавання всіх пар їхніх відповідних елементів.

Приклад.

+.

Ясно, що операція додавання матриць асоціативна і комутативна, оскільки вона зводиться до додавання елементів матриць. Крім того, А+ θ = θ +А = А, .

Добутком матриці А=[a_ik] на число λ називають матрицю B=[b_ik], де b_ik=λa_ik. Записують B=λA.

Множення матриці на число зводиться до множення всіх її елементів на число.

Приклад.

5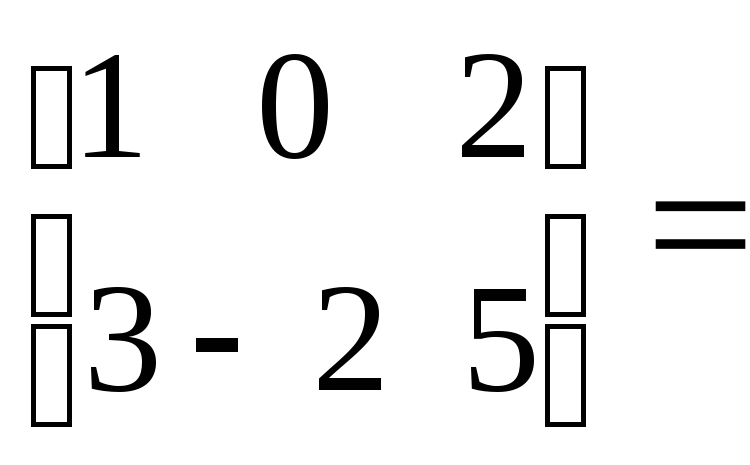

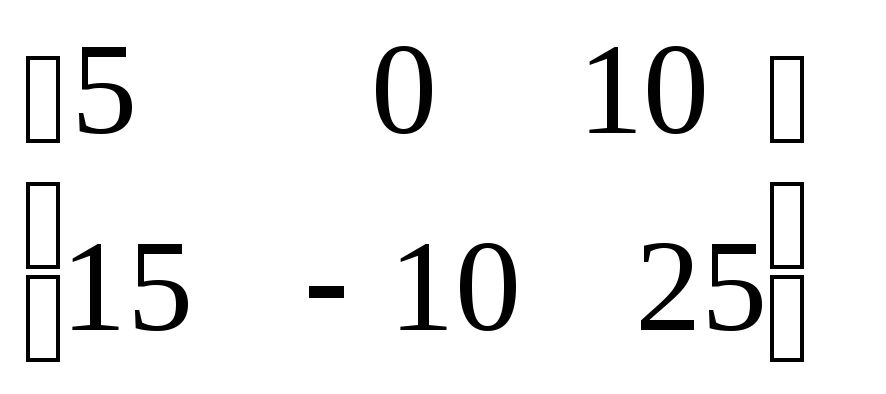
Множення матриці на число асоціативне і дистрибутивне як відносно додавання матриць, так і відносно додавання чисел:

R =;

;

.

Для означення поняття добутку матриць розглянемо питання про послідовне виконання лінійних перетворень змінних.

Нехай х₁,х₂,…,x_n - упорядкований набір змінних, значеннями яких можуть бути довільні числа,

B= _

довільно вибрана (s,n)-матриця з дійсними елементами.Утворимо такі вирази:

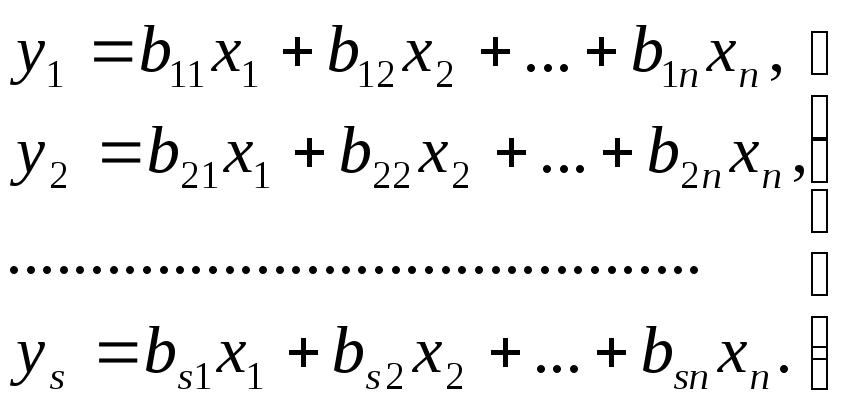
Ясно, що y₁,_,y₂,…,y_n теж є змінними, оскільки вони змінюються залежно від зміни x₁,x₂,…,x_n. Записаний перехід від системи змінних x₁,x₂,…,x_n до системи змінних y₁,y₂,…,y_n називається лінійним перетворенням змінних x₁,x₂,…,x_n у змінні y₁,y₂,…,y_n. Зрозуміло, що це лінійне перетворення повністю визначається своєю матрицею В.

Виконаємо тепер послідовно два лінійних перетворення. Нехай другим перетворенням буде лінійне перетворення змінних y₁,y₂,…,y_n в змінні z₁,z₂,…,z_n:

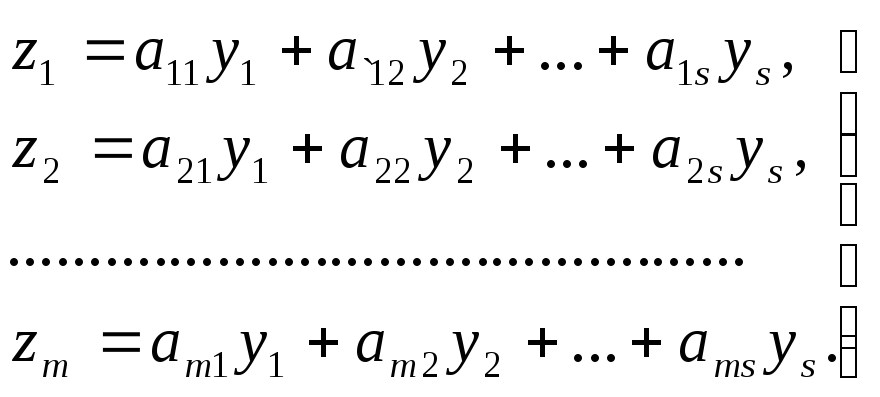
Матриця цього перетворення має вигляд : A=.

Виразимо тепер змінні z₁,z₂,…,z_m через змінні x₁,x₂,…,x_n, підставивши у другі співвідношення значення y₁,y₂,…,y_s із перших.

z₁=a₁₁(b₁₁x₁+b₁₂x₂+…+b_1nx_n)+a₁₂(b₂₁x₁+b₂₂x₂+…+b_2nx_n)+…+a_1s(b_s1x₁+b_s2x₂+…+b_snx_n)=

=(a₁₁b₁₁+a₁₂b₂₁+…+a_1sb_s1)x₁+(a₁₁b₁₂+a₁₂b₂₂+…+a_1sb_s2)x₂+…+(a₁₁b_1n+a₁₂b_2n+…+a_1sb_sn)x_n,

z₂=a₂₁(b₁₁x₁+b₁₂x₂+…+b_1nx_n)+a₂₂(b₂₁x₁+b₂₂x₂+…+b_2nx_n)+…+a_2s(b_s1x₁+b_s2x₂+…+b_snx_n)=

=(a₂₁b₁₁+a₂₂b₂₁+…+a_2sb_s1)x₁+(a₂₁b₁₂+a₂₂b₂₂+…+a_2sb_s2)x₂+…+(a₂₁b_1n+a₂₂b_2n+…+a_2sb_sn)x_n,

……………………………………………………………………………………….

z_m=a_m1(b₁₁x₁+b₁₂x_2+…+b_1nx_n)+a_m2(b₂₁x₁+b₂₂x₂+…+b_2nx_n)+…+a_ms(b_s1x₁+b_s2x₂+…+b_snx_n)=

=(a_m1b₁₁+a_m2b₂₁+…+a_msb_s1)x₁+(a_m1b₁₂+a_m2b₂₂+…+a_msb_s2)x₂+…+(a_m1b_1n+a_m2+…+a_msb_sn)x_n.

Якщо подати отримані співвідношення у вигляді

z₁=c₁₁x₁+c₁₂x₂+…+c_1nx_n

z₂=c₂₁x₁₊c₂₂x₂+…+c_2nx_n

_{………………………………………..}

z_m=c_m1x₁+c_m2x₂+…+c_mnx_nm,

то c_ik=_ijb_jk, де i=1,2,…,m; k=1,2,…,n.

Як видно, результат послідовного виконання двох лінійних перетворень змінних теж є лінійним перетворенням змінних.

Матриця С результуючого лінійного перетворення має вигляд

С =

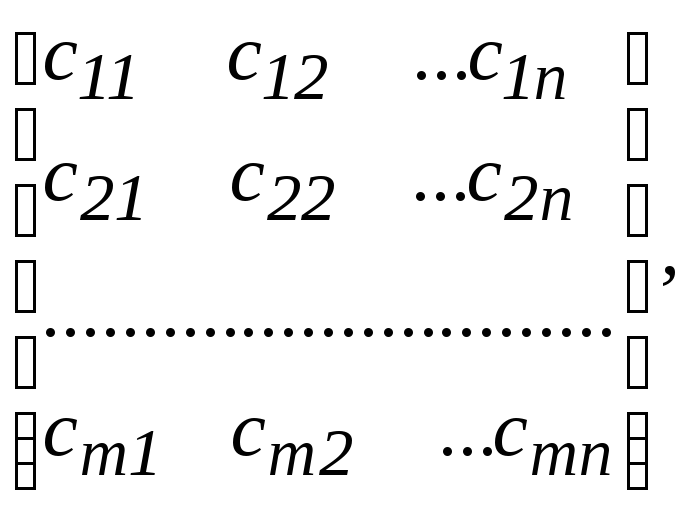
де c_sk == a_і1b_1k+ a_i2b_2k +…+ a_isb_sk (i=1,2,…,m; k=1,2,…,n).

Матрицю С і називають добутком матриці А на матрицю В. Позначають С=АВ. Зрозуміло, що множити матриці можна тільки тоді, коли кожен рядок матриці А містить стільки елементів, скільки їх у кожному стовпчику матриці В.

Приклад.

=.

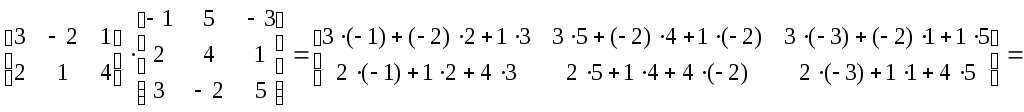Ясно, що множення матриць некомутативне. Операція множення матриць асоціативна і дистрибутивна відносно додавання:

(АВ)С=А(ВС);

(А+В)С=АС+ВС;

С(А+В)=АС+СВ.

5