Б) Операції над лінійними перетвореннями

Сумою двох лінійних перетворень А та ℬ називається таке перетворення А+В, при якому

Властивості:

1. А+В = В+А.

2. (А+В)+С = А+(В+С).

3. А+ Ơ = А.

Добутком лінійного перетворення А на число α називається таке теж лінійне перетворення αА, при якому

Властивості:

1. 1·А = А.

2. α(βА)=(αβ)А.

3. (α+β)А=αА+βА.

4. α(А+В)=αА+αВ.

Добутком лінійних перетворень А та В називається таке теж лінійне перетворення АВ, при якому

Властивості:

1. (АВ)ℂ=А(Вℂ).

2. Аℰ=А.

3. (А+В)ℂ=Аℂ+Вℂ.

4. ℂ(А+В)=ℂА+ℂВ.

Для кожного невиродженого лінійного перетворення А існує таке (обернене до А) лінійне перетворення А^-1, що

А∙А^-1=А^-1·А=ℰ.

Ясно, що добуток невироджених лінійних перетворень теж є невиродженим лінійним перетворенням.

В) Перехід до нового базису

Нехай лінійне перетворення А в базисі е=(е₁,е₂,…,е_п) має матрицю А, а в базисі - матрицю . Знайдемо зв’язок між ними.

Позначимо через С матрицю переходу від базису е до базису . Тоді

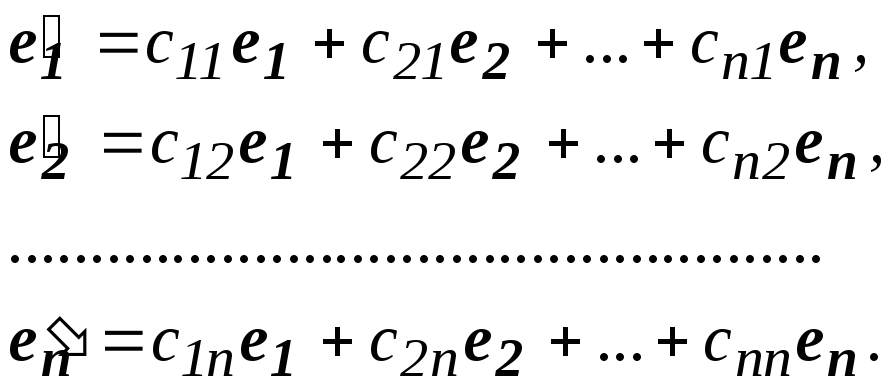
Будемо матрицю С розглядати як матрицю лінійного перетворення ℂ в базисі е. Тоді

Значить, лінійне перетворення ℂ переводить вектори базису е у вектори базису . Відомо, що визначник матриці С відмінний від нуля, значить, дляℂ існує обернене перетворення ℂ ^-1, при якому

За умовою,

.

Застосуємо до обох частин цієї рівності перетворення ℂ ^-1:

.

Підставимо в ліву частину :

,

тобто матрицею перетворення в базисіе є матриця Але, з другого боку матриця цього перетворення рівна добутку матриць відповідних перетворень в базисіе, тобто .

Ясно, що визначник матриці лінійного перетворення не залежить від базису:

Приклад.

В базисі е₁,е₂ перетворення А має матрицю

Написати матрицю цього перетворення в базисі

Розв’язування.

Матриця переходу ТодіЗвідси

Г) Ранг і дефект лінійного перетворення

Сукупність всеможливих векторів вигляду Ах, де , називаєтьсяобластю значень або образом лінійного перетворення А. Позначається ImА.

Сукупність всеможливих векторів , для якихАх=0, називається ядром лінійного перетворення А. Позначається KerА.

І образ, і ядро лінійного перетворення А є підпростором в V.

а) Якщо тох=Ах₁, у=Ау₁, де тох+у=Ах₁+Ау₁=А(х₁+у₁), де і, значить,.

αх=αАх₁=А(αх₁), де і, значить,.

Отже, ImА – підпростір простору V.

б) Якщо , тобто якщоАх=0 і Ау=0, то і

А(х+у)= Ах+Ау=0+0=0 і

А(αх)=αАх=α·0=0,

тобто і

Отже, KerА – підпростір простору V.

Розмірність образу перетворення А dim(ImА) співпадає з рангом матриці А цього перетворення і називається рангом перетворення А. Дійсно, підпростір ImА породжується векторами Ае₁, Ае₂,..., Ае_п, де е={e₁, e₂,…,e_n} – довільний базис простору V і, значить, розмірність ImА дорівнює максимальній кількості лінійно незалежних стовпчиків матриці А.

Розмірність ядра dim(KerА) називається дефектом лінійного перетворення А.

Важливим є твердження, що сума рангу і дефекту лінійного перетворення А дорівнює розмірності п простору V. Тобто,

dim(ImА)+dim(KerА)=n.

Д) Інваріантні підпростори

Нехай V₁ – підпростір векторного простору V, А – деяке лінійне перетворення простору V. Образ Ах вектора х із V₁ не обов’язково належить V₁.

Розглянемо такі підпростори, вектори яких не виводяться із них перетворенням А.

Підпростір V₁ простору V називається інваріантним відносно лінійного перетворення А, якщо образ Ах кожного вектора х із V₁ належить V₁.

Приклади.

1. Для лінійного перетворення А – повороту навколо осі Оz звичайного тривимірного простору - інваріантними підпросторами будуть, наприклад, площина хОу і вісь Оz.

2. Для лінійного перетворення А – ортогонального проектування того ж простору на площину хОу - інваріантними підпросторами будуть: площина хОу; всі площини, що проходять через вісь Оz; сама вісь Оz; всі прямі площини хОу, що проходять через початок координат.

3. В довільному просторі кожний підпростір інваріантний відносно тотожнього і нульового перетворень.

4. В довільному просторі при довільному лінійному перетворенні сам простір і його підпростір, що складається із одного нульового вектора, є інваріантними.

Теорема 1. Перетин і сума підпросторів, інваріантних відносно лінійного оператора А, інваріантні відносно А.

Доведення.

а) Якщо підпростори V₁ і V₂ інваріантні відносно А і , то і , значить, і , тобто .

б) Якщо , тоx=v₁+v₂, де ,. Тодіі, звідкиАх=Аv₁+Аv₂▲

Теорема 2. Якщо А – невироджене лінійне перетворення і V₁ – підпростір, інваріантний відносно А, то V₁ інваріантний і відносно А^-1.

Доведення.

Нехай е₁, е₂, …, е_r – базис підпростору V₁. Тоді вектори

Ае₁, Ае₂, …, Ае_r, які із інваріантності V₁ теж належать V₁, теж лінійно незалежні і, значить, теж утворюють базис V₁, тобто довільний вектор можна через цей базис виразити: