§2. Лінійні перетворення а) Основні поняття

Кажуть, що в лінійному просторі VзаданоперетворенняА, якщо кожному векторупоставлений у відповідність деякий векторА(х) (пишутьАх). ВекторАхназиваютьобразомвекторах.

Перетворення А називаєтьсялінійним, якщо для довільних двох векторівхтауізVі довільного дійсного числаαвиконуються рівності:

1. А(х+у)=Ах+Ау,

2. А(αх)=αАх.

Виберемо в просторі V довільний базисе=(е₁,е₂,…,е_п).Тоді деякий вектор в цьому базисі розкладеться так:

х=х₁е₁+х₂е₂+…+х_пе_п,

де х₁,х₂,…,х_п–компоненти векторахв даному базисі. ОскількиА– перетворення лінійне , то

Ах=А(х₁е₁+х₂е₂+…+х_пе_п)=х₁Ае₁+х₂Ае₂+…+х_пАе_п.

Оскільки Ае_і (і=1,2,…,п)– теж вектори ізV, то їх можна розкласти за вибраним базисом:

Ае₁=а₁₁е₁+а₂₁е₂+…+а_п1е_п,

Ае₂=а₁₂е₁+а₂₂е₂+…+а_п2е_п,

…………………………………

Ае_п=а_1пе₁+а_2пе₂+…+а_ппе_п,

звідки

Ах=х₁(а₁₁е₁+а₂₁е₂+…+а_п1е_п)+х₂(а₁₂е₁+а₂₂е₂+…+а_п2е_п)+…+х_п(а_1пе₁+а_2пе₂+…+а_ппе_п)=

=(а₁₁х₁+а₁₂х₂+…+а_1пх_п)е₁+(а₂₁х₁+а₂₂х₂+…+а_2пх_п)е₂+…+(а_п1х₁+а_п2х₂+…+а_ппх_п)е_п.

Якщо координатами вектора Ахв базисіеєтобто

,

то із єдиності розкладу вектора за базисом отримаємо:

а₁₁х₁+а₁₂х₂+…+а_1пх_п,

а₂₁х₁+а₂₂х₂+…+а_2пх_п,

………………………………

а_п1х₁+а_п2х₂+…+а_ппх_п.

Звідси випливає, що кожному лінійному перетворенню Ав заданому базисіевідповідає цілком певна матриця

стовпчиками якої є коефіцієнти розкладу векторів Ае_і (і=1,2,…,п) за базисом е і рядками якої є коефіцієнти розкладу вектора Ах за координатами вектора х.

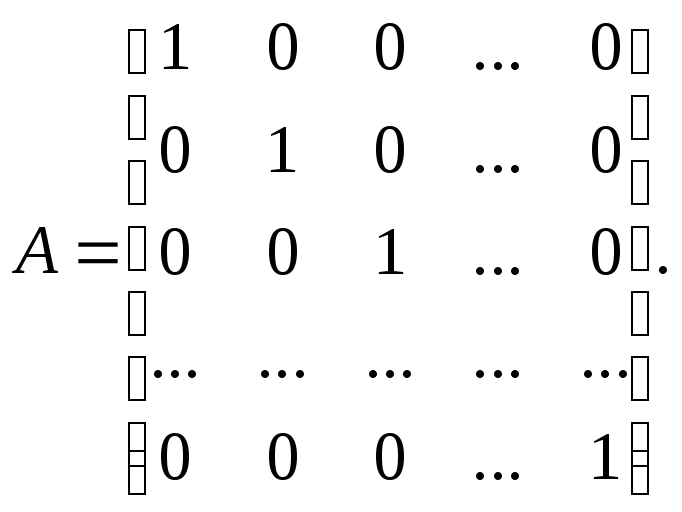
Ясно, що в п-вимірному векторному просторі V кожна квадратна матриця п-го порядку є матрицею деякого лінійного перетворення.

Матрицю А називають матрицею лінійного перетворення. Лінійне перетворення називається виродженим (невиродженим), якщо його матриця вироджена (невироджена).

При невиродженому лінійному перетворенні лінійно незалежні вектори переходять в лінійно незалежні вектори.

Дійсно, якщо вектори е₁,е₂,…,е_k лінійно незалежні і

,

то (із невиродженості А)

і α₁=α₂=…=α_k=0 (за умовою).

Отже, вектори Ае₁,Ае₂,…,Ае_k теж лінійно незалежні, що й треба довести.▲

Приклади.

1. Нехай А – поворот всіх векторів площини хОу навколо початку координат на кут φ проти годинникової стрілки. Припустимо, що базисні вектори – одиничні і взаємно ортогональні. Вектор Ае₁ – одиничний, він утворює з е₁ кут φ, з е₂ – кут . Значить,Ае₁=cosφ·е₁+sinφ·e₂. Вектор Ае₂ – теж одиничний, він утворює з е₁ кут зе₂ – φ. Значить, Ае₂=sinφ·e₁+cosφ·e₂. Отже,

2. Нехай А – ортогональне проектування на площину хОу. Це перетворення лінійне, оскільки проекція суми векторів дорівнює сумі проекцій доданків, проекція добутку вектора на число дорівнює добутку проекції вектора на це число. Якщо в ролі базису вибрано одиничні вектори е₁,е₂,е₃ прямокутної декартової системи координат, то Ае₁=е₁, Ае₂=е₂, Ае₃=0, і, значить,

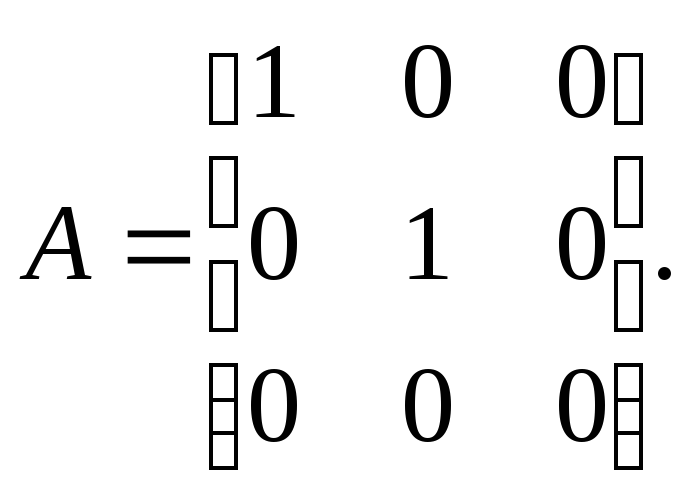
3. Нехай ℰ – тотожнє перетворення векторного простору V, яке визначається рівністю ℰх=х для всіх Тодіℰе_і=е_і для всіх і=1,2,…,п, і, значить,

4. Нехай Ơ – так зване нульове перетворення векторного простору V, яке визначається рівністю Ơх=0 для всіх . Матриця цього перетворення є нульовою і

Перетворення 1 і 3 – невироджені, 2 і 4 – вироджені.