Вакарчук І.О. Квантова механіка

Рис. 55. Надтонке розщеплення для основного стану атома водню.

Експериментальне значення вiдповiдної частоти випромiнювання при розщепленнi рiвня енерґiї для основного стану атома водню (n = 1, l = 0, m = 0):

ν = /2π~ = 1420405751.768 ± 0.002 Гц,

а довжина хвилi

λ 21 см.

Електричнi квадрупольнi переходи (0′–0-переходи) мiж цими рiвнями є

забороненими, тому це магнiтне дипольне випромiнювання. У виразi для вiдповiдної ймовiрностi переходу при врахуваннi спiну електрона необхiдно зро-

бити замiну ˆ на ˆ + 2ˆ .

L L se

“Лiнiя 21 см” вiдiграє важливу роль у радiоастрономiї, оскiльки за нею визначають розподiл атомарного водню у Всесвiтi. Цiкаво також, що саме на цiй довжинi хвилi проводять пошук iнших позаземних цивiлiзацiй6.

6“Лiнiю 21 см” у радiоспектрi Галактики вперше передбачив у 1944 роцi

тодi нiкому невiдомий голландський студент Гендрик ван де Гюлст у Лейденi. Весною 1951 року її експериментально виявили Гарольд Юен i Едвард Парсел у США, а за кiлька тижнiв в Австралiї та Голландiї. У голландцiв, якi мали розрахунки ван де Гюлста, перед початком спостережень виникла пожежа i частина апаратури згорiла. Потративши час на її вiдновлення, вони прийняли випромiнювання на три мiсяцi пiзнiше за американцiв.

531

§ 64. Час життя збуджених станiв атомiв. Природна

ширина спектральних лiнiй

Знайденi вирази для iнтенсивностей випромiнювання та поглинання свiтла атомними системами говорять про те, що спектральнi лiнiї є безмежно вузькими i мають дельтаподiбний характер. Тобто атом випромiнює на певнiй фiксованiй частотi ω = (E2 − E1)/~, що вiдповiдає квантовим переходам мiж станами |1i та |2i, якi ми вважаємо стацiонарними. Iншими словами, ми при-

пускали, що електрон, рухаючись в атомi, у деякому зв’язаному станi може перебувати безмежно довго. Насправдi, стацiонарним станом є лише основний стан атомної системи. Усi збудженi стани є квазiстацiонарними через певний час атом спонтанно переходить iз збуджених станiв у стани з нижчою енерґiєю i, врештiрешт, в основний стан, якому вiдповiдає найменше значення енерґiї. Час перебування атома в збудженому станi називають часом життя цього квазiстацiонарного стану. Причиною спонтанних переходiв є взаємодiя атомної системи з нульовими коливаннями електромагнiтного поля. Мовою класичної електродинамiки, причиною спонтанних переходiв є взаємодiя заряду з полем, яке вiн сам випромiнює, так звана реакцiя випромiнювання. Квазiстацiонарнiсть збуджених станiв приводить до того, що спектральнi лiнiї iзольованої атомної системи є не безмежно вузькими, а мають деяку ширину, яку називають природною шириною спектральної лiнiї. Мiжатомна взаємодiя та тепловi рухи атомiв спричинюють подальше розширення спектральних лiнiй.

Теорiя природної ширини спектральних лiнiй є тонким i аж нiяк не простим питанням. Почнемо з класичного розгляду. На рухомий заряд, що випромiнює, дiє сила Лоренца, створена електромагнiтним полем самого заряду. Вираз для цiєї сили можна знайти прямим обчисленням, використовуючи запiзнюючi потенцiали Лiєнара–Вiхерта для електромагнiтного поля точкового заряду e. Вираз, який отримуємо для сили, що дiє на заряд, можна розкласти в ряд за степенями 1/c (див., наприклад, В. Гайтлер.

Квантовая теория излучения. М.: ИЛ, 1956):

532

де ε0 власна електростатична енерґiя заряду, v його швид-

кiсть, а крапками над лiтерами позначенi похiднi за часом. Слiд зазначити, що цей розклад є асимптотичним.

Запишемо рiвняння руху для заряду маси m0, ураховуючи силу реакцiї випромiнювання та зовнiшню силу f:

Множник бiля прискорення

4 ε0 m = m0 + 3 c2

має змiст спостережувальної маси заряду. Внутрiшня неузгодженiсть класичної електродинамiки проявляється в тому, що електромагнiтна частина маси 4ε0/3c2 для точкового заряду є величиною безмежною ε0 c2/r0, r0 → 0. Уважається, що ця безме-

жнiсть компенсується безмежнiстю, яка формується силами неелектромагнiтного походження в m0 (наприклад, сили Казимира), i в результатi ми спостерiгаємо скiнченну величину m.

Другий доданок у виразi для fL приводить до гальмування

руху випромiнюючого заряду. Наприклад, для квазiпружної зовнiшньої сили f = −mω02r розв’язок рiвняння руху дає загасаючi

коливання7

r(t) = r0 cos(ωt + δ) e−γt/2

з частотою ω = ω0 − 5γ2/8ω0 i сталою загасання

2e2ω2

γ= 3 mc30 .

Урезультатi iнтенсивнiсть поглинання енерґiї таким осцилятором

не матиме дельтаподiбного характеру в околi частоти ω0, а буде функцiєю частоти з гострим максимумом у точцi ω0.

Перейдемо до квантового опису. Рiвняння Шрединґера для хвильової функцiї ψ(q, t) описує, як ми знаємо, явища зворотнi в часi: замiна t на (−t) приводить до рiвняння для комплексно

7Див. вiдступ наприкiнцi цього параграфа.

533

спряженої хвильової функцiї ψ (q, t). Здавалось би, що воно та-

ким чином не спроможне пояснити скiнченний час життя атома в збудженому станi, а тим самим i природну ширину спектральних лiнiй. Однак це можливо зробити, якщо вiдбирати потрiбнi нам розв’язки. Почнемо з простих феноменологiчних мiркувань.

Хвильову функцiю атома ψ = ψ(q, t) розкладаємо в ряд за

повною системою функцiй, що описує стацiонарнi стани:

ψ(q, t) = X Cne− ~i Entψn(q),

n

де, згiдно з принципом суперпозицiї, коефiцiєнт |Cn|2 дорiвнює ймовiрностi знаходження атома в станi ψn.

Для простоти розгляньмо дворiвневий атом зi станами: основним |1i = ψ1 i збудженим |2i = ψ2. У системi, що складається iз сукупностi N таких атомiв, маємо

N2 = N|C2|2

атомiв у збудженому станi. Унаслiдок висвiчування кiлькiсть атомiв у збудженому станi зменшується за законом, який природно записати так:

−dNdt2 = N2w2→1,

де w2→1 iмовiрнiсть квантового переходу за одиницю часу атома зi збудженого стану |2i в основний стан |1i. Тобто ми вважаємо,

що швидкiсть зменшення числа атомiв у збудженому станi пропорцiйна їхнiй кiлькостi в цьому станi.

Це рiвняння вже є незворотним у часi й дає

N2 = Ne−γt,

де стала загасання γ = w2→1. Звiдси випливає, що

|C2|2 e−γt

i коефiцiєнти розкладу залежать вiд часу:

C2 e−γt/2.

534

У загальному випадку врахування спонтанних переходiв, коли Cn e−γnt/2, як бачимо, приводить до того, що стацiонарних ста-

нiв

ψn(q, t) = e− ~i Entψn(q)

не iснує, а маємо квазiстацiонарнi стани:

ψn(q) = e− ~i Ent− γ2n t,

множник з γn дає їх загасання.

Причому декремент загасання γn можна пiдрахувати як iмовiрнiсть переходу зi стану n у стани, що є нижчими, тобто мають

меншi значення енерґiї. Час життя атома у збудженому станi

τn = 1/γn.

Оскiльки γn визначається як iмовiрнiсть переходу, що пропорцiйна до “числа фотонiв плюс одиниця”, то час життя τn залежить

ще й вiд iнтенсивностi електромагнiтного поля. Коли фотони вiдсутнi, то маємо лише спонтаннi переходи на нижчi рiвнi внаслiдок взаємодiї з нульовими коливаннями поля. Очевидно, що для основного стану, як стану з найменшою енерґiєю, величина γ0 = 0, а τ0 = ∞ стацiонарний стан. Цiкаво, що врахування квазiста-

цiонарностi квантових станiв формально можна здiйснити, якщо енерґiю вважати комплексною величиною: En → En − i~γn/2.

Iнтенсивнiсть випромiнювання без урахування квазiстацiонарностi станiв була пропорцiйною до дельта-функцiї δ(Ef −Ei), яка у виразi для ймовiрностi переходу за одиницю часу wi→f забезпечує

виконання закону збереження енерґiї. Тепер, якщо при виведеннi

535

γ = γf + γi.

Отже, таке розмивання δ-функцiї приводить до того, що спе-

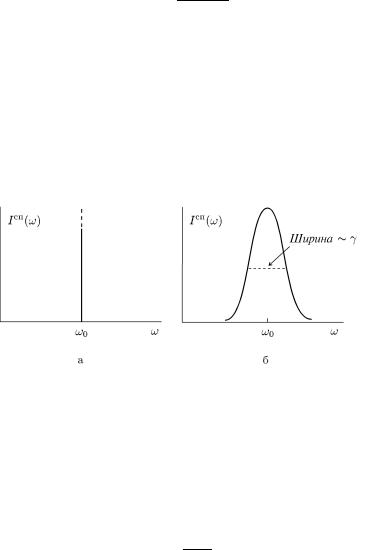
ктральнi лiнiї мають скiнченну ширину: дельтаподiбний профiль замiнюється профiлем, який називають контуром Лоренца (див. рис. 56). Ця ширина має назву “природна ширина спектральної лiнiї”. Отже, наслiдком квазiстацiонарностi атомних станiв є те, що атом випромiнює не на певнiй частотi ω0, а в iнтервалi частот в околi ω0.

Рис. 56. Профiлi атомної спектральної лiнiї: а δ-подiбний; б з урахуванням квазiстацiонарностi станiв.

Для оцiнки γ у випадку дворiвневого атома скористаймось ви-

разом для iнтенсивностi спонтанного випромiнювання (див. §61), який iз точнiстю до множника ~ω дорiвнює величинi w2→1, пiд-

сумованiй за хвильовим вектором i поляризацiєю фотона, а отже, дорiвнює величинi γ:

I(ω) γ = ~ω ,

536

γ= 4 ω3 |d12|2.

3 c3~

Зробимо чисельну прикидку. Матричний елемент дипольного моменту атома d12 ea, де “розмiри” атома a aB = ~2/me2, тому

Отже,

γ

ω

де стала тонкої структури α 1/137. Таким чином, вiдношення

ωγ 10−7.

Коли характернi частоти ω 1015 сек−1, то час життя атома в збудженому станi τ 10−8 сек.

Якщо дипольнi переходи забороненi, то час життя збiльшується в (λ/a)2 разiв. Атом у збудженому станi живе протягом10−2 сек i бiльше. Такi стани, як ми вже говорили, називають

метастабiльними.

Перейдемо тепер до побудови строгої теорiї природної ширини спектральної лiнiї. Для розрахунку спектральної густини енерґiї нам уже недостатньо звичайної теорiї збурень, як це робилось ранiше при вивченнi процесiв поглинання й випромiнювання свiтла. Необхiдно переформулювати теорiю збурень так, щоб розв’язок рiвняння Шрединґера мав вигляд e−γt/2, який ми встановили

“феноменологiчним” шляхом.

Пригадаємо загальнi формули нестацiонарної теорiї збурень:

X

ψ(q, t) =

m

~ ˙

X

i Cm =

n

537

Конкретизуємо задачу: нехай ми маємо дворiвневий атом плюс електромагнiтне поле. “Нульова” задача це атом i поле, якi не взаємодiють. Нехай у початковий момент часу t = 0 атом знаходиться в станi |2i з енерґiєю E2, а фотони вiдсутнi, тобто стан поля описується хвильовою функцiєю вакууму |0, . . . , 0i. Кiнцевий стан: атом знаходиться на нижньому рiвнi |1i з енерґiєю E1, i поле характеризується хвильовою функцiєю |0, . . . , 0, 1k,α, 0, . . . , 0i з наявнiстю одного фотона з хвильовим вектором k та поляризацiєю α.

Отже, початкова хвильова функцiя

|ii = |2i|0, . . . , 0i,

а кiнцева

|fi = |1i|0, . . . , 0, 1k,α, 0, . . . , 0i.

Нагадаймо також, що оператор збурення

а при t → ∞ величина Ci → 0. Виберемо розв’язок для Ci в

такому виглядi:

Ci = e− 2 t,

де невiдома величина, яку необхiдно знайти. З наших загаль-

них формул маємо

538

Причому пiдсумовування за промiжними iндексами n це пiдсумовування за k та α. Випишемо також рiвняння для Cf i отрима-

ємо таку систему:

i~Cf = CiVfi.

Не враховуючи в другому рiвняннi переходи “вверх” (тобто поглинання фотона), ми тим самим вiдбираємо розв’язки рiвняння Шрединґера, якi описують еволюцiю лише прямого переходу, тобто вносимо в цей процес незворотнiсть у часi. Виправданням цього може бути лише те, що взаємодiя фотона й атома з переходом атома в збуджений стан вiдбувається за дуже великий час (порiвняно з атомним часом). Образно кажучи, фотон iз дуже малою ймовiрнiстю зустрiне знову “свiй” атом. Хоча, урештi-решт, мандруючи Всесвiтом, вiн i провзаємодiє з цим атомом. Приклад таких блукаючих фотонiв ми маємо це релiктовi фотони (релiктове випромiнювання)8.

Iнтеґруємо друге рiвняння з урахуванням вибраної форми роз- в’язку для Ci:

1e− 2 t+iωfit − 1

=i~Vfi iωfi − /2 ,

де частота

8Релiктове електромагнiтне випромiнювання випадково виявили в 1965 ро-

цi американськi радiоастрономи А. А. Пензiас i Р. В. Вiльсон (Нобелiвська премiя 1978 року). Вони конструювали антени з якомога меншими власними шумами й дiйшли до певної межi, якої не могли понизити. Виявилось, що цей докучливий шум i є релiктовими фотонами.

539

ωfi = ωk − ω0.

Повернемось тепер до першого рiвняння системи:

Оскiльки Ci = e− 2 t, то з нього випливає рiвняння для невiдомої величини :

(як швидкоосцилююча функцiя вона не дає внеску) . Далi вико-

9“Коли Бог створив час, то Вiн створив його досить” iрландське прислiв’я. Ми часто використовуємо граничний перехiд t → ∞ як математичну операцiю. Фiзично ця безмежнiсть означає, що величина t, тобто час дiї збу-

рення, є набагато бiльшою, нiж деякий характерний для конкретної задачi масштаб часу, наприклад, обернена частота переходу мiж квантовими станами атома. Отже, ми кожного разу припускаємо, що часу є досить, щоб забезпечити цей граничний перехiд, i що квантова система живе довше, нiж величина характерного масштабу часу. Однак ситуацiя може бути й зовсiм iншою, якщо мова йде про фемтосекундну (10−15 сек) чи аттосекундну (10−18 сек)

спектроскопiю, коли час тривання лазерного iмпульсу збурення є меншим, нiж перiод коливань електромагнiтної хвилi.

540