Таким чином, згідно з Основною теоремою

,

де – довільні сталі, є загальним розв’язком рівняння (2).

Випадок 2. Всі характеристичні числа різні, але серед них є ком­плексні. Нехай – комплексне характеристичне число рівняння (5).

,

Таким чином, якщо всі характеристичні числа рівняння (5) різні, але серед них є комплексні, то кожному дійсному числу відповідає розв’язок , а кожній парі комплексно-спряжених чисел від­по­­відають два дійсні лінійно незалежні частинні розв’язки і . Всього одержуємо n дійсних частин­них розв’язків вигляду

, , , (6)

Метод Ейлера побудови ФСР і загального розв’язку одно­рід­ного лінійного рів­няння у випадку кратних характе­ристичних чисел. Нехай – характеристичне число рів­нян­ня (5) (дійсне або комплекс­не) кратності s.

Це означає, що функції

(9)

є розв’язками рівняння (2).

Якщо характеристичне рівняння (5) має комплексний корінь кратності s, то воно має спряжений комплексний корінь тієї ж кратності. Згідно з (9), кореню відповідають s розв’язків

.

Ці розв’язки комплексні. Відокремлюючи в них дійсні та уявні частини, одержуємо 2s дійсних розв’язків:

7. Лінійні неоднорідні рівняння.Розглянемо лінійне неоднорідне рівняння

(1)

і відповідне йому однорідне рівняння . (2)

Теорема 1. Загальний розв’язок неоднорідного рівняння (1) дорівнює сумі будь-якого частинного розв’язку цього рівняння та загального розв’язку відповідного однорідного рівняння (2).

Теорема 2. Нехай права частина неоднорідного рівняння (1) є сумою двох доданків, тобто це рівняння має вигляд .(6).Якщо – частинний розв’язок рівняння , а – частинний розв’язок рівняння , то сума є частинним розв’язком рівняння (6).

Метод варіації довільних сталих (метод Лагранжа).

Нехай маємо загальний розв’язок однорідного рівняння (2):, (7),де – деяка ФСР рівняння (2), а – довільні сталі.Частинний розв’язок р-я (1) шукаємо у вигляді (7), але розглядаємо як деякі ф-ї змінної x: (8)

Таким чином, шукані функції задовольняють систему

Маємо неоднорідну систему n лінійних алгебраїчних рівнянь з n невідомими . Оскільки її визначником є вронскіан , то ця система має єдиний розв’язок . Інте­груючи, знаходимо функції , після чого їх залишиться підста­вити у формулу (8).

Метод невизначених коефіцієнтів. Розглянемо неодно­рідне лінійне рівняння n-го порядку зі сталими коефіцієнтами:

(10)

де – сталі дійсні числа, функція неперервна на .

Розглянемо деякі випадки, пов’язані у виглядом функції .

Випадок 1. Права частина рівняння (10) є добутком многочлена на показникову функцію, тобто:

(11)

де

(12)

є многочленом з дійсними або комплексними коефіцієнтами (він може бути й сталою), – стале дійсне або комплексне число.

Випадок 1.1. Число не є коренем характеристичного рівнян­ня, тобто ( – характеристичний многочлен (лекція 12)). Тоді частин­ний розв’язок Y шукаємо у вигляді

, (13)

де – многочлен m-го степеня з невизначеними коефіцієнтами.

Скоротимо на і прирівняємо коефіцієнти біля однакових степенів x:

(16)

Оскільки , то з системи (16) послідовно визначаються всі коефіцієнти , і причому однозначно.

Випадок 1.2. Число є коренем кратності k характеристичного рівняння, тобто

, але . (17)

У цьому випадку частинний розв’язок Y у вигляді (13) не побудувати, бо . Тепер шукатимемо його у вигляді

, (18)

де 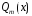– многочлен m-го степеня з невизначеними коефіцієнтами, які визначаються так само, як і випадку 1.1.

Прирівнюючи коефіцієнти біля однакових степенів x, одержуємо:

Оскільки , то з цих рівностей можна послідовно визначити всі коефіцієнти .