1. Однорідні рівняння та звідні до них.

Функцію називають однорідною виміру m, якщо для довільних 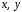і t справджується тотожність

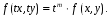
Якщо (12) виконується лише для , то функцію називають додатно однорідною. Якщо диференціальне рівняння першого порядку записане у вигляді

, (14)

то воно буде однорідним, якщо функції і однорідні одного і того ж виміру m (m може бути довільним дійсним числом).

Однорідне рівняння зводиться до рівняння з відокремлюваними змінними. Для цього зробимо заміну ,де – нова шукана функція. Тоді

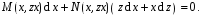(15)

. (16)

,

(17)

.

Замінивши в (17) z на частку , одержуємо загальний інтеграл однорідного рівняння (14) у вигляді

.

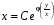Відокремлюючи змінні у рівнянні (16), можна втратити розв’язки вигляду 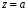, де a – корінь рівняння .

Підставляючи ці значення z у формулу 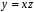, одержуємо, що півпрямі 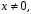які примикають до початку координат, є розв’язками однорідного рівняння. Ці розв’язки можуть бути особливими. Особливими розв’язками також можуть бути півосі : 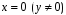. Інших особливих розв’язків немає.

Рівняння, звідні до однорідних.

Розглянемо рівняння , (1)

де – деякі числа. Будемо вважати, що , тобто хоч одне з чисел не дорів­нює нулю, бо інакше права частина рівняння (1) буде одно­рідною функцією виміру 0, а самė рівняння – однорідним

Розглянемо два випадки.

Випадок 1. Нехай 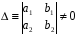.Зробимо заміну змінних , (2)де – нові змінні, – поки що довільні сталі.

,

. (3)

Виберемо тепер сталі так, щоб вони були розв’язком неодно­рідної системи лінійних алгебраїчних рівнянь

Оскільки за припущенням , то ця система має єдиний розв’язок, який можна знайти, н-д, за формулами Крамера. Тоді з (3) одержуємо ДР (4),яке є однорідним. Зінтегрувавши рівняння (4) за допомогою заміни 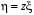,де 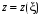– нова функція, і повернувшись до змінних x і y за формулами , які випливають з (2), знайдемо загальний інтеграл рівняння (1).

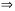
Випадок 2. Нехай . Тоді .Якщо позначити , то , а тому рівняння (1) запишеться у вигляді (5)Рівняння (5) – це рівняння вигляду інтегрується за допомогою заміни .

2. Лінійні рівняння та звідні до них

Диференціальне рівняння вигляду 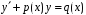(6)

називають лінійним. Будемо вважати, що функції , неперервні на деякому інтервалі .

Якщо в (6) для всіх , то воно має вигляд

(7)

і його називають лінійним однорідним Рівняння (6), в якому тотожно не дорів­нює нулю, нази­вають лінійним неоднорідним.

Для цього використаємо метод варіації довільної сталої (метод Лагранжа¹⁾). Зінте­груємо спочатку лінійне однорідне рівняння (7). Відокрем­люючи у ньому змінні, одержуємо:

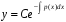, (8)

де С – довільна стала. Формула (8) описує всі розв’язки рівняння (7), бо розв’язок , який міг бути втраченим при відокремленні змінних, міститься в загальному розв’язку (8) (якщо ).

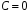. (9)

Для знаходження функції С(x) підставимо (9) у (6). Тоді

.

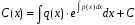Підставляючи знайдене значення С(x) в формулу (9), одержуємо формулу для загаль­ного розв’язку лінійного рівняння:

. (10)

Рівняння Бернуллі. Рівняння вигляду

, (11)

називають рівнянням Бернуллі. Випадки та не розгля­да­­ємо, бо для цих значень m рівняння (11) є лінійним. Вважатимемо, що функції і 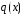неперервні на деякому інтервалі .

Рівняння Бернуллі завжди може бути зведене до лінійного рівняння. Для цього, так само, як і для лінійного рівняння, викорис­таємо метод варіації довільної сталої.

Зінтегруємо спочатку рівняння . Його загальний роз­в’язок задається форму­лою

.

Розв’язок рівняння Бернуллі шукатимемо у вигляді

, (12)

де 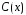– деяка функція. Підставляючи (12) у (11), одер­жуємо:

.

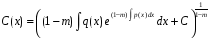Підставляючи знайдену функцію у (12), одержуємо загальний розв’язок рівняння Бернуллі:

.

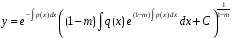При цьому міг бути втрачений розв’язок , якщо 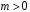. Якщо ж , то цей розв’язок буде особливим, а якщо , то частинним. Для функція 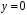не є розв’язком рівняння (11).

3. Рівняння у повних диференціалах. Рівняння вигляду (1),називають рівнянням у повних диференціалах, якщо його ліва части­на є пов­ним диференціалом деякої функції , тобто якщо .(2).З (1), (2) випливає, що рівняння у повних диференціалах можна записати у вигляді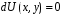,а тому його загальним інтегралом є 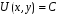. Особливих розв’язків рівняння у повних диференціалах, очевидно, не має. Припустимо, що функції M, N мають неперервні похідні . .(4). Умова (4) є необхідною для того, щоб ліва частина рівняння (1) була повним диференціалом. Таким чином, загальний інтеграл рівняння (1) можна записати у вигляді (7).Якщо, будуючи функцію , взяти за вихідну другу з рівностей (3), то одержимо інший вираз для загального інтеграла рівняння (1), а саме (8)

Інтегрувальний множник. Функцію називають інтегрувальним множником рівняння (1), якщо рівняння (10),в області G є рівнянням у повних диференціалах. Умови на функції і 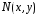: вони неперервні разом з частинними похідними і 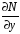в деякій однозв’язній області G і у жодній точці цієї області одночасно не перетворюються в нуль. Від інтегрувального множника вимагатимемо, щоб від не перетворювався в нуль і мав неперервні частинні похідні першого порядку.(11).

Для знаходження функції одержали рівняння (11), задача інтегрування якого є досить складною. Однак у деяких випадках рівняння (11) вдається легко розв’язати.

Випадок 1. Нехай – інтегрувальний множник рівняння (1). .,де, наприклад, можна покласти Випадок 2. Нехай – інтегрувальний множник рівняння (1). _, Знаючи інтегрувальний множник, можна знайти не тільки загальний інтеграл рівняння, але й всі його особливі розв’язки.