
- •1. Множина дійсних чисел. Упорядкованість, щільність, повнота множини дійсних чисел.
- •2. Числова послідовність. Види числових послідовностей. Границя послідовності. Властивості збіжних послідовностей.
- •3.Неск-но малі і неск-но великі посл-ті, спів. Між ними. Леми про нескінченно малі.
- •4. Відповідність. Відоброження, функція. Способи задання. Види функції.
- •5.Границя функції в розумінні Гейне та Коші. Еквівалентність означень. Визначні границі: .
- •6.Неперервність функції в точці. Різні означення. Одностороння неперервність і її зв’язок з неперервністю в точці.
- •8.Задачі, які приводять до поняття похідної. Означення похідної. Таблиця похідних. Геометричний та механічний зміст. Правила відшукання похідних. Похідна композиції функцій.
- •9.Застосування похідної до дослідження функції на сталість, монотонність.
- •10. Локальний екстремум функції. Необхідна умова. Достатні умови. Знаходження найбільшого і найменшого значення функції на сегменті
- •11. Напрям опуклості графіка функції. Достатні умови. Точка перегину. Необхідна умова перегину. Достатні умови.
- •12.Первісна функція (неозначений інтеграл). Таблиця основних інтегралів. Інтегрування підстановкою, частинами.
- •13.Інтеграл Рімана. Необхідна умова. Необхідна і достатня умова інтегрованості. Класи інтегрованих функцій. Теорема Ньютона-Лейбніца.
- •16. Частинні похідні, диференційованість функції багатьох змінних. Достатня умова диференційованості. Диференціал функції. Правила диференціювання.
16. Частинні похідні, диференційованість функції багатьох змінних. Достатня умова диференційованості. Диференціал функції. Правила диференціювання.
Нехай
функція
 визначена в деякому околі точки
визначена в деякому околі точки .
Надамо змінній х
приросту
.
Надамо змінній х
приросту
 ,
залишаючи змінну
,
залишаючи змінну
 незмінною, так, щоб точка
незмінною, так, щоб точка належала заданому околу. Величина
належала заданому околу. Величина називаєтьсячастинним
приростом
функції
називаєтьсячастинним
приростом
функції по змінній х. Аналогічно вводиться
частинний приріст
по змінній х. Аналогічно вводиться
частинний приріст функції по змінній
функції по змінній :
: Якщо
існує границя
Якщо
існує границя
 то
вона називаєтьсячастинною
похідною функції
то
вона називаєтьсячастинною
похідною функції
 в точці
в точці по
змінній
по
змінній і позначається
одним із таких символів:
і позначається
одним із таких символів:
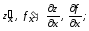
 – частинні похідні по
– частинні похідні по в точці
в точці .Аналогічночастинна
похідна функції
.Аналогічночастинна
похідна функції
 по
по визначається як границя
визначається як границя і
позначається одним із символів:
і
позначається одним із символів: Згідно
з означенням, при знаходженні частинної
похідної
Згідно
з означенням, при знаходженні частинної
похідної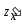 обчислюють
звичайну похідну функції однієї змінної
обчислюють
звичайну похідну функції однієї змінної
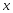 ,
вважаючи змінну
,
вважаючи змінну
 сталою, а при знаходженні похідної
сталою, а при знаходженні похідної сталою вважається змінна
сталою вважається змінна .
Тому частинні похідні знаходять за
формулами і правилами обчислення
похідних функцій однієї змінної. Частинна
похідна
.
Тому частинні похідні знаходять за
формулами і правилами обчислення
похідних функцій однієї змінної. Частинна
похідна (або
(або )
характеризує швидкість зміни функції
в напрямі осі
)
характеризує швидкість зміни функції
в напрямі осі
 (або
(або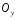 ).
З'ясуємо
геометричний зміст частинних похідних
функції двох змінних. Графіком функції
).
З'ясуємо
геометричний зміст частинних похідних
функції двох змінних. Графіком функції
 є
деяка поверхня. Графіком функції
є
деяка поверхня. Графіком функції
 є лінія перетину цієї поверхні з площиною
є лінія перетину цієї поверхні з площиною .
Виходячи з геометричного змісту похідної
для функції однієї змінної, дістанемо,
що
.
Виходячи з геометричного змісту похідної
для функції однієї змінної, дістанемо,
що
 ,
де
,
де – кут між віссю
– кут між віссю і дотичною, проведеною до кривої
і дотичною, проведеною до кривої в точці
в точці .
Аналогічно
.
Аналогічно .
Для функції
.
Для функції
 змінних можна знайти
змінних можна знайти частинних
похідних:
частинних
похідних:
 де
де
 ,
, .
.
Щоб
знайти частинну похідну
 треба взяти звичайну похідну функції
треба взяти звичайну похідну функції по змінній
по змінній ,
вважаючи решту змінних сталими. Якщо
функція
,
вважаючи решту змінних сталими. Якщо
функція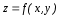 задана в області
задана в області і має частинні похідні
і має частинні похідні в усіх точках
в усіх точках ,
то ці похідні можна розглядати як нові
функції, задані в області
,
то ці похідні можна розглядати як нові
функції, задані в області .
Тому має сенс питання про існування
частинних похідних від цих функцій по
якій-небудь змінній в точці
.
Тому має сенс питання про існування
частинних похідних від цих функцій по
якій-небудь змінній в точці .Якщо
існує частинна похідна по
.Якщо
існує частинна похідна по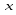 від функції
від функції ,
то її називаютьчастинною
похідною другого
порядку від функції
,
то її називаютьчастинною
похідною другого
порядку від функції
 по змінній
по змінній і позначають
і позначають
 або
або .
Таким
чином, за означенням
.
Таким
чином, за означенням
 або
або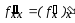 Якщо існує частинна похідна по
Якщо існує частинна похідна по від функції
від функції ,
то її називаютьчастинною
похідною другого порядку від функції
,
то її називаютьчастинною
похідною другого порядку від функції
 по змінній
по змінній і позначають
і позначають
 або
або .
Отже, за означенням
.
Отже, за означенням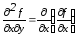 або
або
Для
функції двох змінних
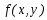 можна розглядати чотири похідні другого
порядку:
можна розглядати чотири похідні другого
порядку:
 .
Якщо
існують частинні похідні від частинних
похідних другого порядку, то їх називають
частинними
похідними третього порядку функції
.
Якщо
існують частинні похідні від частинних
похідних другого порядку, то їх називають
частинними
похідними третього порядку функції
 ,
їх вісім:
,
їх вісім:

 .
.
Числові ряди. Збіжні числові ряди. Необхідна умова збіжності. Необхідна і достатня умова збіжності. Ознаки збіжності додатних рядів.
Нехай дано числову послідовність{un}. Вираз вигляду
а1+а2+…+аn+… (1)
або, те
саме, вигляду
 називаєтьсячисловим
рядом.
Числа u1,u2,…,un,...називаються
членами ряду. З кожним рядом вигляду
(1) будемо ставити у відповідність суми
називаєтьсячисловим
рядом.
Числа u1,u2,…,un,...називаються
членами ряду. З кожним рядом вигляду
(1) будемо ставити у відповідність суми
S1=u1,
S2=u1+u2,
S3=u1+u2+u3 ,
………………. (2)
Sn =u1+u2+…+un ,
………………
які
називаються частинними або частковими
сумами. Частинні суми ряду утв. деяку
числову послідовність{Sn}. Ряд(1) наз.
збіжним, якщо збігається послідовність
його частинних сум{Sn},
тобто якщо існує скінчена границя
 .
Число S- сума ряду. Якщо послід. немає
границі або =
.
Число S- сума ряду. Якщо послід. немає
границі або = ,то
такий ряд наз. розбіжним(ряд не має
суми). Кожній послід. Можна поставити у
відповідність ряд сумS1
,...,Sп,
S1+(
S2
–S1)+(S3-
S2)+...+(Sп-
Sп-1)+...
,то
такий ряд наз. розбіжним(ряд не має
суми). Кожній послід. Можна поставити у
відповідність ряд сумS1
,...,Sп,
S1+(
S2
–S1)+(S3-
S2)+...+(Sп-
Sп-1)+...
Теорема(необхідна
умова збіжності ряду):
Якщо ряд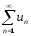 збігається,
то його п- тий член прямує до нуля при
збігається,
то його п- тий член прямує до нуля при :
:
Доведення.
Нехай
 ,тоді
,тоді (3). За умовою теореми, ряд
(3). За умовою теореми, ряд збігається, а це означає, що існує
скінчена границя
збігається, а це означає, що існує
скінчена границя .
Звідси і з (3) випливає правильність
рівності
.
Звідси і з (3) випливає правильність
рівності .
.
Теорема доведена.
Розгл.
критерій Коші для послідовності для
доведення не достатності умови теореми.
Нехай дано 1)
 ;
2)
;
2) ,тоді
для
,тоді
для >0
>0 ,що
при n>N,m>N
,що
при n>N,m>N
Щоб ряд
1) був збіжн. необх. і дост ,щоб
 ,
р- довіл.
,
р- довіл.
З цього
випливає , що якщо ряд збіжний , то його
n-тий член прямує до 0 при
 (це
є необх умова збіжн.)
(це
є необх умова збіжн.)
При р=1

 .
Це озн. не буде дост. для
.
Це озн. не буде дост. для ряду.Необхідна
і достатня ознака збіжності ряду.
ряду.Необхідна
і достатня ознака збіжності ряду.
Теорема:
Дано ряд
 Щоб ряд був збіжний необх. і достат.,
щоб послідовність його частинних сум
була обмежена , тобто
Щоб ряд був збіжний необх. і достат.,
щоб послідовність його частинних сум
була обмежена , тобто
Довед.
Необх.
Якщо ряд збіжний ,то
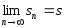 .Оск. послідовність
.Оск. послідовність має границю, то ця послід. обмежена.
має границю, то ця послід. обмежена.
Дост.
Дано, що послідовність обмежена
 ,
причому
,
причому .
Оскільки послідовність монотонно
зростає і є обмеженою , то вона має
границю.Теорему
доведено.
.
Оскільки послідовність монотонно
зростає і є обмеженою , то вона має
границю.Теорему
доведено.
Ознаки збіжності додатніх рядів
Ряд
 ,
де
,
де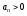 – називається додатнім. Додатній ряд
завжди має суму; ця сума буде скінченною
(і, відповідно, ряд – збіжним), якщо
частинні суми ряду обмежені зверху, і
нескінченною (а ряд –розбіжним)
в протилежному випадку.
– називається додатнім. Додатній ряд
завжди має суму; ця сума буде скінченною
(і, відповідно, ряд – збіжним), якщо
частинні суми ряду обмежені зверху, і
нескінченною (а ряд –розбіжним)
в протилежному випадку.
. I
Якщо маємо (1) (2)
(2)
 і
починаючи з деякого номера
і
починаючи з деякого номера для всіх
для всіх
 ,
і для всіх
,
і для всіх ,
то із збіжності ряду (2) слідує збіж. ряду
(1), а із розбіж. (1) – розбіж. (2).
II
Якщо
,
то із збіжності ряду (2) слідує збіж. ряду
(1), а із розбіж. (1) – розбіж. (2).
II
Якщо

 то 1) при
то 1) при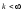 із збіжності ряду (2) слідує збіж. (1); 2)
при
із збіжності ряду (2) слідує збіж. (1); 2)
при із
розбіж. (1) слідує розбіж (2); 3)Якщо
із
розбіж. (1) слідує розбіж (2); 3)Якщо ряди одночасно збіжні або розбіжні.
ряди одночасно збіжні або розбіжні.
Гранична озн.
Раабе. Якщо
 то
ряд (1)
то
ряд (1)
 збіжний. Якщо
збіжний. Якщо
 то
ряд (1)
то
ряд (1)
 розбіжний.
розбіжний.
Інтегральна
ознака Маклорена. Якщо
ряд (1) такий, що по
 можна знайти
функцію
можна знайти
функцію
 таку,
що
таку,
що
 ,
, і
спадна, тоді
і
спадна, тоді
 іряд
)
іряд
) одночасно
збіжні або розбіжні.
одночасно
збіжні або розбіжні.
. 2. Нехай
 збіжний. Існує
збіжний. Існує збіж.
збіж. границя скінченна і ряд (1) збіжний.3.
Нехай (1) розбіжний. Це означає, що
границя скінченна і ряд (1) збіжний.3.
Нехай (1) розбіжний. Це означає, що
 ,
тому
,
тому ,
,

 .
Отже, ряд розбіжний.
.
Отже, ряд розбіжний.
Нехай
 розбіжний,
то
розбіжний,
то .
За означенням,
.
За означенням, тому і ряд
розбіжний. Ознака доведна.
тому і ряд
розбіжний. Ознака доведна.
III.
Якщо
починаючи з деякого номера
 для
всіх номерів
для
всіх номерів
 виконується нерівність
виконується нерівність ,
то із збіжності ряду (2) слідує збіж. (1),
із розбіж. (1) – розбіж. (2).
,
то із збіжності ряду (2) слідує збіж. (1),
із розбіж. (1) – розбіж. (2).
Ознака Даламбера.
Якщо починаючи
з деякого номера
 для всіх
номерів
для всіх
номерів

 то ряд (1)
то ряд (1) збіжн. Якщо починаючи з деякого номера
збіжн. Якщо починаючи з деякого номера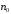 для всіх
номерів
для всіх
номерів
 то ряд розбіжний.
то ряд розбіжний.
Озн. Коші.
Розгул. варіанта Коші
 .Якщо,
починаючи з деякого номера
.Якщо,
починаючи з деякого номера


 то ряд(1)
то ряд(1) збігається.
Якщо, починаючи з деякого номера
збігається.
Якщо, починаючи з деякого номера



 ,
то ряд(1)
,
то ряд(1) розбіжний.
розбіжний.
Гранична ознака
Коші. Якщо
 ,
то ряд (1)
,
то ряд (1) збігається. Якщо
збігається. Якщо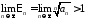 ,
то ряд(1)
,
то ряд(1) розбіжний.
Якщо
розбіжний.
Якщо
 ,
то про збіжність чи розбіжність не
можна судити за цією ознакою.
,
то про збіжність чи розбіжність не
можна судити за цією ознакою.
Ознака Раабе.
Розгл. Варіанта Раабе
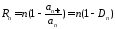 .
Якщо, починаючи з деякого номера
.
Якщо, починаючи з деякого номера

 ,
то ряд(1)
,
то ряд(1) збіжний.
Якщо
збіжний.
Якщо
 ,
то ряд розбіжний.
,
то ряд розбіжний.
