
- •1. Множина дійсних чисел. Упорядкованість, щільність, повнота множини дійсних чисел.
- •2. Числова послідовність. Види числових послідовностей. Границя послідовності. Властивості збіжних послідовностей.
- •3.Неск-но малі і неск-но великі посл-ті, спів. Між ними. Леми про нескінченно малі.
- •4. Відповідність. Відоброження, функція. Способи задання. Види функції.
- •5.Границя функції в розумінні Гейне та Коші. Еквівалентність означень. Визначні границі: .
- •6.Неперервність функції в точці. Різні означення. Одностороння неперервність і її зв’язок з неперервністю в точці.
- •8.Задачі, які приводять до поняття похідної. Означення похідної. Таблиця похідних. Геометричний та механічний зміст. Правила відшукання похідних. Похідна композиції функцій.
- •9.Застосування похідної до дослідження функції на сталість, монотонність.
- •10. Локальний екстремум функції. Необхідна умова. Достатні умови. Знаходження найбільшого і найменшого значення функції на сегменті
- •11. Напрям опуклості графіка функції. Достатні умови. Точка перегину. Необхідна умова перегину. Достатні умови.
- •12.Первісна функція (неозначений інтеграл). Таблиця основних інтегралів. Інтегрування підстановкою, частинами.
- •13.Інтеграл Рімана. Необхідна умова. Необхідна і достатня умова інтегрованості. Класи інтегрованих функцій. Теорема Ньютона-Лейбніца.
- •16. Частинні похідні, диференційованість функції багатьох змінних. Достатня умова диференційованості. Диференціал функції. Правила диференціювання.
5.Границя функції в розумінні Гейне та Коші. Еквівалентність означень. Визначні границі: .
Точка а називається точкою згущення числової множини Х={x}, якщо в будь-якому її околі містяться відмінні від а значення хєХ. Нехай задана функція f(x) в області визначення X , і задана точка a, яка може і не належати до області визначення.
Означення 1 "за Гейне". Число A називається границею функції f(x) в точці x=a, якщо для всякої послідовності x1, x2,…,xn, що збігається до a, відповідна послідовність значень функції f(x1), f(x2),…, f(xn) збіжна до A.
Означення 2 "за
Коші". Число
A
називається границею
функції
f(x)
в точці x=a,
якщо для всякого
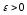 існує таке
існує таке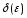 ,
що з нерівності
,
що з нерівності слідує нерівність
слідує нерівність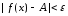 .
.
Еквівалентність означень.
Нехай виконується
означення 2, тобто для всякого
 існує таке
існує таке ,
що з нерівності
,
що з нерівності слідує нерівність
слідує нерівність .
Оберемо з області значень функціїf(x)
послідовність x1,
x2,…,xn–>a.
За означенням границі послідовності
це означає, що для всякого δ>0 існує
N(δ),
що з того що n>N
слідує
.
Оберемо з області значень функціїf(x)
послідовність x1,
x2,…,xn–>a.
За означенням границі послідовності
це означає, що для всякого δ>0 існує
N(δ),
що з того що n>N
слідує
 ,
а згідно нашого припущення, буде вірною
і така нерівність
,
а згідно нашого припущення, буде вірною
і така нерівність ,
а це й означає, що
,
а це й означає, що
Нехай виконується
означення 1, тобто для всякої послідовності
x1,
x2,…,xn,
що збігається до a,
відповідна послідовність значень
функції f(x1),
f(x2),…,
f(xn)
збіжна до A.
Припустимо, що означення 2 не виконується,
тоді існує таке
 ,
що
,
що
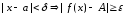 .
Виберемо такі δ1,
δ2…
що:
.
Виберемо такі δ1,
δ2…
що:

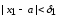


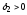



…………………………




Нехай
 ,
тоді
,
тоді ,
а оскільки виконується означення 1, то
це означає, що
,
а оскільки виконується означення 1, то
це означає, що ,
а це протирічить тому, що
,
а це протирічить тому, що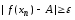 .
Отже, наше припущення невірне.
.
Отже, наше припущення невірне.
Число A
називається границею
функції
f(x)
в точці x=a
зліва (лівосторонньою),
якщо для всякого
 існує таке δ1,
що з нерівності
існує таке δ1,
що з нерівності
 слідує нерівність
слідує нерівність .
.
Число A
називається границею
функції
f(x)
в точці x=a
справа (правосторонньою),
якщо для всякого
 існує таке δ2,
що з нерівності
існує таке δ2,
що з нерівності
 слідує нерівність
слідує нерівність .
.
Теорема. Критерій Коші. Для того щоб функція f(x) мала скінчену границю в точці а необхідно і достатньо щоб:
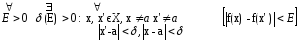
Визначні границі:
 ;
;
 .
.
1. Розглянемо послідовність
Розглянемо послідовність 1…n,
і покажемо ,що вона строго зростає і
обмежена зверху та має скінченну границю.
Застосувавши формулу біному
Ньютона,отримаємо
1…n,
і покажемо ,що вона строго зростає і
обмежена зверху та має скінченну границю.
Застосувавши формулу біному
Ньютона,отримаємо


Із виразу
,який знаходиться у правій частині
рівності ,видно,що при переході від n
до n+1
число доданків у написаній сумі зростає
на одиницю і кожен доданок ,починаючи
з третього,збільшується,так як стає
більшим вираз, який стоїть в кожній
круглій дужці,так як
 Це означає строге зростання послідовності
Це означає строге зростання послідовності Далі , оскільки
Далі , оскільки

2.Доведемо,що
 Розглянемо в координатній площині коло
радіуса R
з центром в початку координат .Якщо
OA=R,
Розглянемо в координатній площині коло
радіуса R
з центром в початку координат .Якщо
OA=R,
 AOB=x,
0<x<
AOB=x,
0<x< \2
,
\2
, ,то
площа
,то
площа
 ,
тобто
,
тобто
 звідси
звідси ,
або
,
або .
В
силу парності функцій
.
В
силу парності функцій
 і
і ця нерівність справедлива і для
ця нерівність справедлива і для .
Переходячи в цій рівності до границі
при
.
Переходячи в цій рівності до границі
при
 і маючи на увазі ,що в силу неперервності
функціїcos
x
при x=0
має місце рівність
і маючи на увазі ,що в силу неперервності
функціїcos
x
при x=0
має місце рівність
 .Отримаємо ,що
.Отримаємо ,що
6.Неперервність функції в точці. Різні означення. Одностороння неперервність і її зв’язок з неперервністю в точці.
Означення 1. Функція називається неперервною в точці x0, якщо вона в цій точці існує, існує границя функції в цій точці і має місце рівність
 .
.
Функція
f(x)
називається неперервною в точці x=x0,
якщо для всякого

 існує таке
існує таке , яке залежить від
, яке залежить від ,
що з нерівності
,
що з нерівності слідує
слідує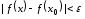 .
.
Щоб функція була неперервною в точці необхідно щоб вона мала границю в цій точці.
Означення. Функція f(x) в точці x0 називається неперервною зліва (справа), якщо лівостороння (правостороння) границя дорівнює значенню функції в цій точці.
 ,
,
Якщо функція неперервна зліва і справа, то вона неперервна в цій точці.
Теорема 1. Якщо функції f(x) i g(x) визначені в одному і тому проміжку Х і неперервні в точці х0, то в цій точці будуть неперервними і функції:
f(x)±g(x), f(x)·g(x), f(x)/g(x) (g(x)≠0).

…………………………………………….
Теорема 2. Нехай функція φ(y) визначена на проміжку уєУ, а функція y=f(x) – хєХ. Причому коли хєХ то уєУ.
Якщо функція f(x) неперервна в точці х0, а функція φ(х) неперервна – у0=f(x), то складна функція φ(f(x)) теж буде неперервною в точці х0.

Що й буде свідчити про неперервність складної функції в точці х0. ■
Якщо функція в точці x0 не неперервна, то ця точка називається точкою розриву функції. Розриви функції поділяються на розриви першого і другого роду.
Якщо в точці x0 існують границі зліва і справа, але не рівні, або навіть рівні, але не дорівнюють значенню функції в цій точці, то це розрив першого роду.
Якщо не існує хоч одна з односторонніх границь або рівні ∞, то це розрив другого роду.
Серед розривів першого роду виділяють усувний розрив – це розрив, коли обидві границі існують і рівні, але не рівні значення функції в цій точці (найчастіше тому, що вона в цій точці не існує). Щоб усунути розрив треба доозначити або переозначити значення функції в цій точці.
7. Властивості неперервної функції на сегменті. Теореми Больцано-Коші, Веєрштраса, Кантора.
Озн. Функція f(x) називається неперервною в т. х0 якщо нескінченно малому приросту аргументу відповідає нескінченно малий приріст ф-ції.
Озн.
Функція f(x)
наз-ся неп-ою
зліва, якщо
 і неп-ю з права, якщо
і неп-ю з права, якщо
Якщо ф-ція неперервна в т. х0 , то вона неперервна в ній і справа, і зліва, і навпаки з неперервності ф-ції f(x) в т. х0 справа і зліва випливає її неперервність у заданій точці.
Т.(І теорема Больцано-Коші)Якщо функція f(x) визначена і неперервна в замкненому проміжку ab і на кінцях цих проміжків приймає значення різних знаків, то між a і b знайдеться точка с в, якій f(x) перетв-ся в 0.
f(x), x
є
[а,b]
 ;
f(c)=0,
f(a)<0,
f(b)>0
;
f(c)=0,
f(a)<0,
f(b)>0
Д:.
Припустимо,
що f(a)<0,
f(b)>0
. Поділимо
[а,b]
пополам
[а;(a+b)/2]
[(a+b)/2;b]
f((a+b)/2)=0.
З двох
отриманих відрізків принаймні на одному
ф-ія на кінцях набуватиме різних значень.
[а1,b1]
– відрізок
на якому функція на кінцях набуватиме
різних значень. [а1,b1]
, f(a1)<0,
f(b1)>0.
Відрізок
[а1,b1]
ділимо пополам [а1;(a1+b1)/2]
[(a1+b1)/2;b1].
Якщо
(a1+b1)/2=0
теорема закінчена, якщо ні то той відрізок
де на якому ф-ія на кінцях набуває різних
знаків. [а,b],
f(an)<0,
f(bn)>0;
[а,b] [а1,b1]
[а1,b1] [а2,b2]
[а2,b2] …
… [аn,bn];
bn-an=(b-a)/2n
[аn,bn];
bn-an=(b-a)/2n n
n 0; b1-a1=(b-a)/2;
b2-a2=(b1-a1)/2=(b-a)/22.
За лемою
про вкладені відрізки одрежуємо, що
0; b1-a1=(b-a)/2;
b2-a2=(b1-a1)/2=(b-a)/22.
За лемою
про вкладені відрізки одрежуємо, що
 ;
; ;
; ;
звідси випливаєf(x)=0
;
звідси випливаєf(x)=0
Т.(ІІ теорема Больцано-Коші)Нехай функція f(x) визначена і неп-на в деякому проміжку Х. Якщо в деяких двох точках цього проміжку х=а, х=b (a<b) функція набуватиме не рівних значень f(a)=A, f(b)=B, то для будь-якого числа с яке міститься між а і b така, що f(c)=c.
Д: f(x), xєX; x=a, x=b; f(a)=A, f(b)=B; x=c, f(c)=C. Нехай А<B. Розглянемо допоміжну ф-ію φ(x)=f(x)-c, ф-ія φ(x) буде неперервною в проміжку Х, як різниця двох неперервних ф-ій. φ(a)=f(a)-c=A-c<0, φ(b)=f(b)-c=B-c<0. За І теорема Больцано-Коші існуватиме точка с між а і b така, що φ(с)=0 => f(c)-c=0 =>f(c)=c
Т.(І теорема
Веэрштраса)Якщо
функція f(x)
визначена і неп-на в замкненому проміжку
ab,то
вона обмежена в цьому проміжку.

Д:
Припустимо,
що ф-ія f(x)
необмежена в проміжку (a,b).
 .За лемою
Больцано-Веєрштраса
.За лемою
Больцано-Веєрштраса
 ,x0є[a,b]
,x0є[a,b]
f(xnk)->
f(x0),
f(xnk) .Суперечність,
доводить, що ф-ція буде обмежена на
[a,b].
.Суперечність,
доводить, що ф-ція буде обмежена на
[a,b].
Т:(ІІ теорема Веэрштраса)Якщо функція f(x) визначена і неперервна в замкненому проміжку ab, то вона досягає в цьому проміжку свого найбільшого і найменшого значення.
Т. Кантора.
Якщо функція
 визначена і неперервна в замкнутому
інтервалі
визначена і неперервна в замкнутому
інтервалі ,
то вона на цьому інтервалі рівномірно
неперервна.
,
то вона на цьому інтервалі рівномірно
неперервна.
Д.
(Від супротивного). Нехай для будь-якого
визначеного
 не існує
не існує ,
про яке йдеться в означенні рівномірної
неперервності. В такому разі
,
про яке йдеться в означенні рівномірної
неперервності. В такому разі .
.
Візьмемо тепер
послідовність
 додатніх чисел так, що
додатніх чисел так, що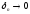 .
Тоді за вище сказаним отримаємо:
.
Тоді за вище сказаним отримаємо:
 .
.
За лемою
Больцана-Веєрштрасса із обмеженої
послідовності
 можна виділити підпослідовність, яка
буде збігатися до деякої точки
можна виділити підпослідовність, яка
буде збігатися до деякої точки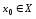 .
Щоб не ускладнювати позначення,
вважатимемо, що сама послідовність
.
Щоб не ускладнювати позначення,
вважатимемо, що сама послідовність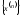 збігається до
збігається до .
.
Так як
 (бо
(бо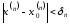 ,
а
,
а ),
то одночасно і послідовність
),
то одночасно і послідовність збігається до
збігається до .
Тоді за неперервністю в функції в точці
.
Тоді за неперервністю в функції в точці ,
має бути:
,
має бути:
 ,
так що
,
так що
 ,а
це протиріччя з тим, що для будь-якого
,а
це протиріччя з тим, що для будь-якого виконується:
виконується: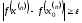 .
Теорема доведена.
.
Теорема доведена.
Озн.
Коливанням
ф-ії f(x)на
деякому проміжку Х
наз-ся величиною
 ;
ω=M-m;
M=supxєX
f(x);
m=infxєX
f(x)
;
ω=M-m;
M=supxєX
f(x);
m=infxєX
f(x)
Наслідок
з теореми Кантора.
Нехай функція
 визначена і неперервна в замкнутому
інтервалі
визначена і неперервна в замкнутому
інтервалі .
Тоді
.
Тоді ,
що якщо інтервал довільно розбити на
проміжки, довжиною меншими за
,
що якщо інтервал довільно розбити на
проміжки, довжиною меншими за ,
то на кожному з них коливання функції
,
то на кожному з них коливання функції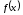 буде меншим за
буде меншим за .
.
