
Множини і дії над ними.
Множиною називають сукупність об’єктів довільної природи(з певними обмеженнями). Множини прийнято позначати великими літерами А, В, …
Ч
 ислові
множини мають стандартне позначенняN-натуральні
числа, Z-цілі
числа, R-дійсні,Q
– раціональні, C-комплексні.
Множина без елементів називається
порожньою і позначається
ислові
множини мають стандартне позначенняN-натуральні
числа, Z-цілі
числа, R-дійсні,Q
– раціональні, C-комплексні.
Множина без елементів називається
порожньою і позначається
Множину можна
задати, перелічивши всі її елементи:
А={1,3,5}; N={1,2,3,…}.
Інший спосіб – вказати ознаку, за якою
відбираються елементи множини. {x
| x-парне
додатнє }={2,4,6,…}, якщо ж відбираємо тільки
елементи з деякої множини, то пишемо
так: {у є R|![]() <3}=(-
<3}=(-![]() ,
,![]() ).
).
Кількість елементів множини називається її потужністю і позначається |A|. Якщо множина А містить об’єкт х, то його називаємо елементом А, і пишемо
х є А, а інакше x
![]() А.
А.
Якщо всі елементи
множини А належать множині В, то А
називають підмножиною В і пишемо
![]() .
.
Н-ад:![]() .Порожня
множина є елементом кожної множини.
.Порожня
множина є елементом кожної множини.
Дії над множинами:
Для довільних двох множин А і В, визначають наступні дії:
Дії над множинами зручно позначати діаграмами Ейлера-Венна.
1)
![]() -об’єднання
множин.
-об’єднання
множин.
Об’єднанням 2-ох множин називається множина всіх елементів, які належать хоча б одній з множин А і В.
2) А![]() -
перетин множин.
-
перетин множин.
Пертином 2-ох множин А і В називають множину елементів спільних для А і В.
3) A \ B – різниця множин.
Різницею 2-ох множин А і В називають множину елементів А, які не належать до В.
4)
![]() =
(А \ В)
=
(А \ В)![]() (В
\ А) - симетрична різниця.
(В
\ А) - симетрична різниця.
Симетричною різницею називають множину елементів, які належать рівно одній з А і В.
Н-ад:
А={1,2,3,4}, В={3,4,5}, тоді
![]() ={1,2,3,4,5},
А
={1,2,3,4,5},
А![]() ={3,4},A
\ B={1,2},
={3,4},A
\ B={1,2},
![]() ={1,2,5}.
={1,2,5}.
Означ.:
Якщо в деякій задачі розглядаємо тільки
елементи деякої множини, то цю множину
називають універсумом. Якщо U
– універсум, то для довільної множини
А, різниця U
\ A
складається з усіх елементів, що не
належать множині А, вона називається
доповненням до А (позначають
![]() ).
).
Н-ад:
U=N,
А={2,4,6,…},
![]() ={1,3,5,…}.
={1,3,5,…}.
Дії над множинами мають очевидні властивості:

 ,
,
 -
комутативний закон.
-
комутативний закон.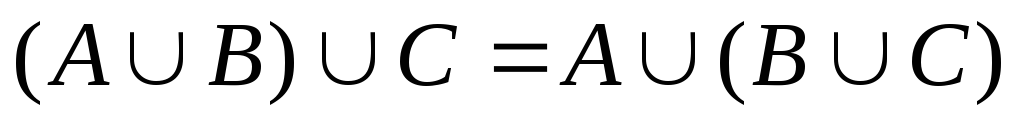 ,
,
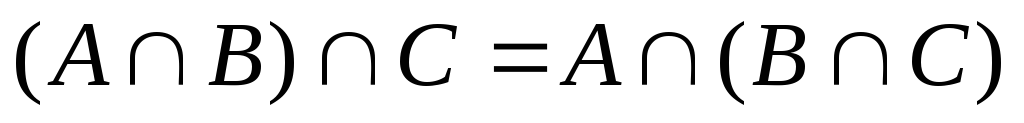 -
асоціативний закон.
-
асоціативний закон.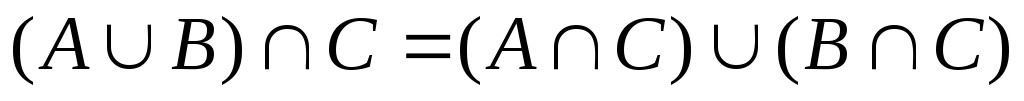 ,
,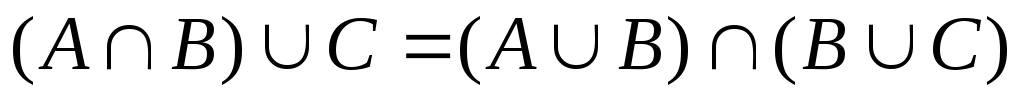 -
розподільні або дистрибутивні закони.
-
розподільні або дистрибутивні закони. ,
,
 - іденпотентність.
- іденпотентність. =А
– інволютивність.
=А
– інволютивність.
Корисними є так звані закони Деморгана:
![]() =
=![]()
![]()
![]() ,
,![]() =
=![]()
![]()
![]()
Дії об’єднання і перетину можливі для довільної кількості множин, при цьому можна використовувати скорочення
![]() або
або
![]()
Відношення та їх властивості.
Озн.:
Відношенням між елементами множин
А1,А2,…,Аn
називаємо довільну підмножину R
декартового добутку A1![]() A2
A2![]() …
…![]() Аn.
Аn.
Оскільки декартів добуток складається з усіх можливих наборів (а1,а2,…,аn), в яких а1є А1, а2 є А2,…,аn є Аn, то відношення складається з усіх або деяких таких наборів, як правило відібраних за деякою ознакою.
Якщо набір (а1,…,аn)
потрапляє до
![]() ,
то кажемо що елементи а1,а2,…,аn
перебувають у відношенні R.
,
то кажемо що елементи а1,а2,…,аn
перебувають у відношенні R.
Якщо відношення пов’язує елементи N-множин, то його називають n-арним (1-множину-унарне,2-ві-бінарне, 3-тернарне).
Н-ад:
![]() -R-бінарне
відношення між елементами множин А={1,2}
і В={x,y},
тоді (1,х) є R-перебувають
у відношенні, (1,у)
-R-бінарне
відношення між елементами множин А={1,2}
і В={x,y},
тоді (1,х) є R-перебувають
у відношенні, (1,у)
![]() R-не
перебувають.
R-не
перебувають.
Як правило, для бінарних відношень замість (х,у) є R пишуть простіше хRу.
Бінарним відношенням
між елементами скінчених множин
зображають також бітовими матрицями
(таблицями). Якщо | A|=m,
|B|=n,
то кожному відношенню
![]() відповідає відношення m
рядків з n
стовпців. Якщо і-тий елемент з А перебуває
у відношенні R
з j-им
елементом множини В, то в і-му рядку на
j-му
місці ставимо одиничку.
відповідає відношення m
рядків з n
стовпців. Якщо і-тий елемент з А перебуває
у відношенні R
з j-им
елементом множини В, то в і-му рядку на
j-му
місці ставимо одиничку.
Бінарне відношення на множині А може мати такі властивості:
рефлексивність
![]() -кожен
ел-т а з множини А перебуває у відношенні
R
сам із собою.
-кожен
ел-т а з множини А перебуває у відношенні
R
сам із собою.
антирефлексивність
![]() -ніякий
ел-т множини А не перебуває у множині R
сам з собою.
-ніякий
ел-т множини А не перебуває у множині R
сам з собою.
симетричність
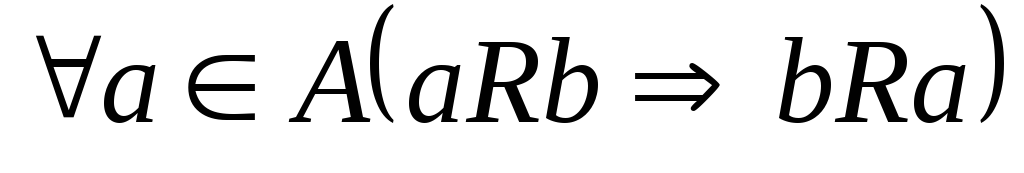 -якщо
а – у від-ніR
з b,
то й b–у
в-ні R
з а.
-якщо
а – у від-ніR
з b,
то й b–у
в-ні R
з а.асиметричність.
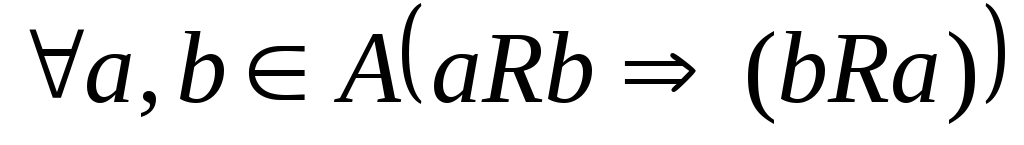 -одночасне
вик-ня аRb
і bRa
– неможл.
-одночасне
вик-ня аRb
і bRa
– неможл.антисиметричність
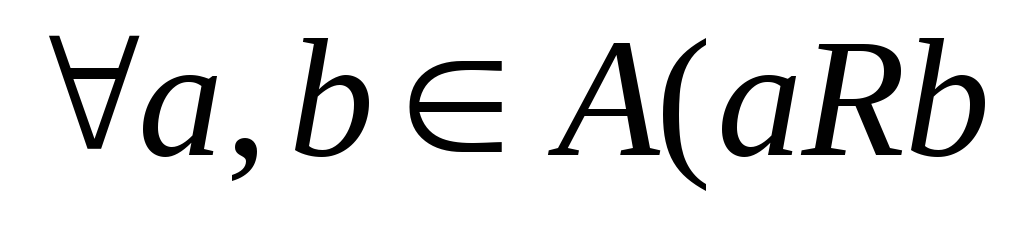 ^
bRa
^
bRa
 a=b)-одночасне
виконання aRb
i
bRa
–неможливе, або можливе при умові їх
рівності.
a=b)-одночасне
виконання aRb
i
bRa
–неможливе, або можливе при умові їх
рівності.транзитивність
![]() (aRb^bRc
(aRb^bRc![]() aRc)-якщо
у відношенні R
перебувають а з b
та b
з с, то а перебуває у відношенні з с.
aRc)-якщо
у відношенні R
перебувають а з b
та b
з с, то а перебуває у відношенні з с.
Бінарне відношення R є :
1.рефлекивне, якщо у його матриці по головній діагоналі розташовані одинички.
2.антирефлексивне, якщо у його матриці по головній діагоналі розташовані нулі
3.симетричне, якщо його матриця теж симетрична відносно головної діагоналі.
4.антисиметричне, якщо у матриці елемент, симетричний до кожної одиниці поза діагоналлю є нулем.
5 асиметричне, якщо у матриці немає 2-ох одиниць симетричних відносно однієї діагоналі, зокрема на самій діагоналі всі елементи є нулями.
3.Відношення часткового порядку.
Озн.:
Бінарне відношення
![]() на
множині х називається відношенням не
строгого порядку, якщо воно рефлексивне,
антисиметричне і транзитивне:
на
множині х називається відношенням не
строгого порядку, якщо воно рефлексивне,
антисиметричне і транзитивне:
![]()
![]() ^
^![]() ,то
х=у
,то
х=у![]() ^
^![]()
![]()
Відношення не
строгого порядку
![]() на
множиніR-
зображається графом, у якому: в кожній
вершині є петля, між різними елементами
не існує одночасно 2-ох протилежних
стрілок, якщо існують дуги з х
в у
і з у
в z,
то існує і дуга з x
в z.
на
множиніR-
зображається графом, у якому: в кожній
вершині є петля, між різними елементами
не існує одночасно 2-ох протилежних
стрілок, якщо існують дуги з х
в у
і з у
в z,
то існує і дуга з x
в z.
Означ.:
Бінарне відношення
![]() на
множиніХ
називається відношенням не строгого
порядку, якщо воно рефлексивне,
антисиметричне і транзитивне:
на
множиніХ
називається відношенням не строгого
порядку, якщо воно рефлексивне,
антисиметричне і транзитивне:
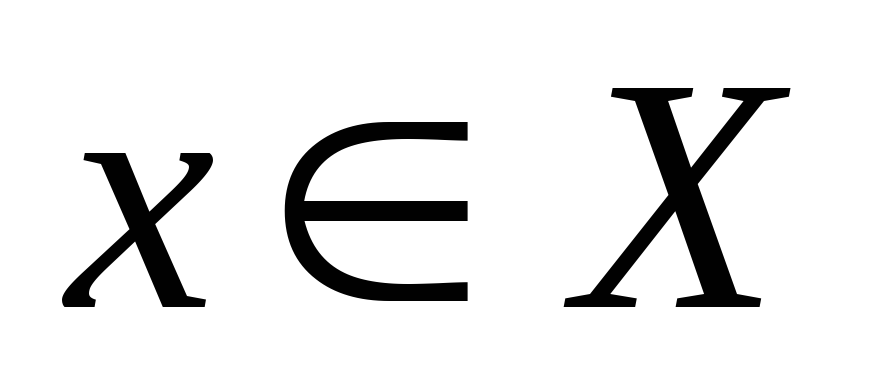 ,
то
,
то
 ;
2)
;
2) ,
то х=у ; 3)х
,
то х=у ; 3)х ,
,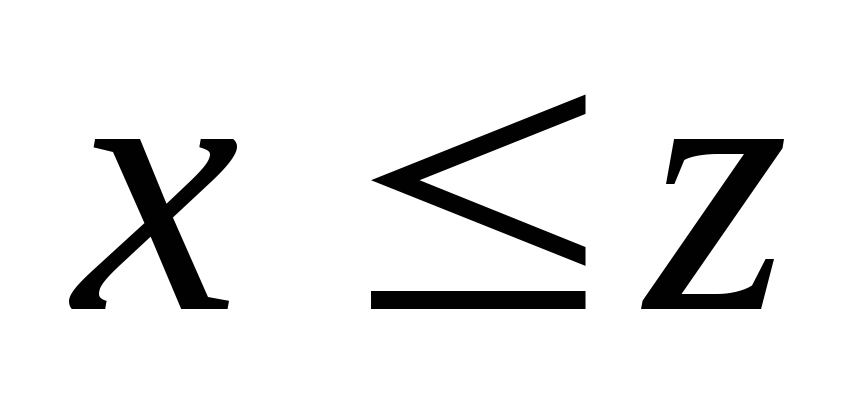
Відношення нестрогого порядку зображається графом, у якому :
1) в кожній вершині є петля; 2) між різними елементами не існує одночасно 2-ох протилежних стрілок;3) якщо існують дуги з х в у і з у в z , то існує і дуга з х в z.
Твердження:
1) Якщо існує
![]() -відношення
строгого порядку, то
-відношення
строгого порядку, то
![]() -
-
![]()
![]() - відношення нестрогого порядку. 2)
- відношення нестрогого порядку. 2)![]() -
відношення нестрогого порядку, то
-
відношення нестрогого порядку, то
![]() -відношення
строгого порядку.
-відношення
строгого порядку.
Якщо для відношення
порядку
![]() і для елементівх
та у
виконано
і для елементівх
та у
виконано
![]() або
або![]() тох
та у
– порівняльні, інакше – не порівняльні.
тох
та у
– порівняльні, інакше – не порівняльні.
Означ.: Частковий порядок, для якого всі пари елементів є порівняльними називають лінійним порядком. Множину з частковим (лінійним) порядком називають частково (лінійно) впорядкованою.
Н-ад:
1)
![]() -відношення
лінійного порядку.
-відношення
лінійного порядку.
Нехай А-підмножина
частково впорядкованої множини
![]() ;
елементb
називають нижньою гранню А, якщо
;
елементb
називають нижньою гранню А, якщо
![]() .
Аналогічно елемент с єX,
с- верхня грань множини то,
.
Аналогічно елемент с єX,
с- верхня грань множини то,
![]() для
всіха
є А.
для
всіха
є А.
П-ад:
Нехай A={3,7,8}![]() ,
тоді 1,2,3 – нижні грані А, 8,9,10-верхні
грані.
,
тоді 1,2,3 – нижні грані А, 8,9,10-верхні
грані.
Означ.:
Елемент х
множини
![]()
![]() називають її найменшими елементом, якщо
називають її найменшими елементом, якщо![]() ,
інакше кажучих
– нижня грань всієї множини Х, у-найбільша,
,
інакше кажучих
– нижня грань всієї множини Х, у-найбільша,
![]() ,
,![]() ,
тодіу
–верхня грань множини Х.
,
тодіу
–верхня грань множини Х.
Означ.:
Елемент х
називається мінімальним min
в множині
![]() ,
якщо не існує
,
якщо не існує![]() (тобто
від нього не існує менших), аналогічно
у-максимумmax,
якщо не існує
(тобто
від нього не існує менших), аналогічно
у-максимумmax,
якщо не існує
![]() .
.
Якщо у множині існує найменший елемент, то він єдиний і одночасно є min, але не навпаки, але не навпаки. Аналогічно, найбільший елемент є максимальний. Найменший і найбільший елементи множини А позначаються min A та max A.
Нехай А-підмножина ЧВМ (частково впорядкована множина).
Означ.: Найбільша серед нижніх граней множини А (якщо вона існує) називається точною нижньою гранню і позначається inf A(інфімум). Аналогічно – найменше з верхніх граней називається точною гранню і позначається sup A(супремум)- точна верхня грань.
П-ад:
Нехай
![]() ,
тоді inf A =2, sup A=3=max A.
,
тоді inf A =2, sup A=3=max A.
Щоб довести, що b=inf A, треба показати, що
b – нижня грань А;
кожна нижня грань А передує
 ,
с є А – з того що
,
с є А – з того що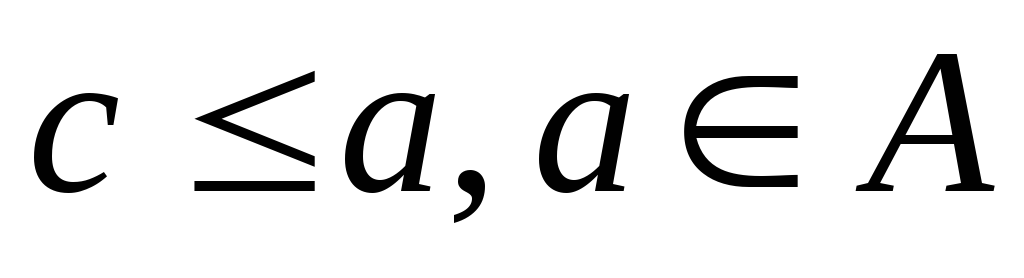 ,
випливає, що
,
випливає, що .
Аналогічно для верхніх граней.
.
Аналогічно для верхніх граней.
Між властивостями
верхніх і нижніх граней є повна подібність.
Це пояснюється тим, що з кожного часткового
порядку
![]() можна утворити протилежний порядок
можна утворити протилежний порядок![]() ,
,![]() -
поклавши, що
-
поклавши, що![]() ,
якщо
,
якщо![]() .
При цьому нижні грані стають верхніми,min-max
і т.д.
.
При цьому нижні грані стають верхніми,min-max
і т.д.
Озн: ЧВМ,
в якій для кожних 2-ох елементів a
i
b
існує іх точна нижня грань inf
{a,b}=a^b
– найбільша серед елементів, що передує
а і b
називається нижньою напівграткою .
Аналогічно верхня напівгратка - це ЧВМ,
така, що а і b
існує точна верхня грань: sup{a,b}=a![]() b(
b(
![]() -cупремум).
-cупремум).
Кожна лінійно
впорядкована множина є нижньою і верхньою
напівграткою : В ЛВМ
-![]() .
.
В нижній напівгратці
взяття точної нижньої грані
![]() є
бінарною операцією
є
бінарною операцією![]()
![]() з
властивостями:
з
властивостями:

 -з
обох боків отримуємо точну нижню грань
множини {x,
y,
z}.
-з
обох боків отримуємо точну нижню грань
множини {x,
y,
z}.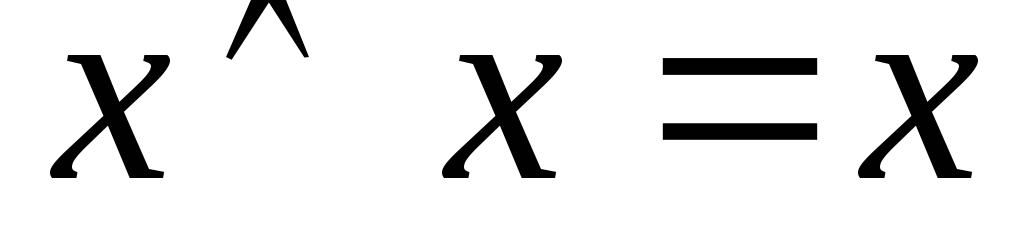 -
властивість іденпотентності.
-
властивість іденпотентності.
Теорема:
Для кожної операції “
* ” :
![]() з властивостями
з властивостями
1) x*y=y*x; 2) x*(y*z)=(x*y)*z; 3) х*х=х.
Існує єдиний
частковий порядок
![]() на х, для якого х*у – це точно нижня грань
-
на х, для якого х*у – це точно нижня грань
-![]() .
.
