Тема 5. Диференціальне числення функції однієї змінної

ЛЕКЦІЯ 15

5. Задачі, що проводять до поняття похідної.

6. Означення похідної.

7. Механічний та геометричний зміст похідної.

8. Односторонні похідні.

9. Нескінченні похідні.

1. Задачі, що проводять до поняття похідної

Задача про миттєву швидкість. Нехай матеріальна точка рухається вздовж прямої. Позначимо відстань точкидо деякої початкової точкиданої прямої в момент часучерез. Тоді в момент часу, де- приріст часу, точкабуде знаходитися на відстані від точкирівній. Різницюназвемо приростом ляху.

Відношення називається середньою швидкістю руху точки за проміжок часу.

Швидкістю руху точки в момент часу або миттєвою швидкістю називається границя відношенняпри, тобто

.

Приклад. Знайти миттєву швидкість рівномірно прискореного руху матеріальної точки з початковою швидкістю і прискоренням.

Розв'язування. Залежність шляху від часупри рівно прискореному русі виражається формулою. Тоді. Отже,

.

Після спрощення одержуємо

.

Таким чином

.

Задача про лінійну густину неоднорідного стержня. Нехай треба знайти густину неоднорідного прямолінійного стержня в точці , яка знаходиться на відстанівід початкової точки(див. рис. 11).

Позначимовеличину маси відрізка. Візьмемо деяку точку, яка знаходиться на відстанівід початкової точки. Тоді маса відрізкабуде рівною. Отже, маса відрізка, яку ми назвемо приростом маси в точці,

.

Відношення називається середньою густиною стержня на відрізкуі позначається.

Лінійною густиною стержня в точці називається границя відношенняпри, тобто

.

Приклад. Нехай маса стержня довжини задається формулою, де- сталі числа. Знайти лінійну густину в точці, яка знаходиться на відстанівід початку стержня.

Розв'язування. Знайдемо приріст маси в точці

.

Отже,

.

Задача про дотичну до кривої. Дотичною до кривої в точціназивається пряма, з якою співпадає граничне положення січноїза умови, що точкапо кривійпрямує до точки(рис. 12).

Зазначимо, що не в кожній точці крива може мати дотичну. В точках, яких крива зазнає зламу, дотична до кривої не існує. Так, наприклад, не існують дотичні у точцікривої(рис. 13), точцікривої(рис. 14), точцікривої(рис. 15).

Розглянемо криву, яка задана в системі координат рівнянням, денеперервна функція, визначена на деякому проміжку. Поставимо задачу: знайти кутовий коефіцієнтдотичної до кривоїв точці, де(рис. 16).

Візьмемо на кривій точку. Через точкипроведемо січну. Нехай вона утворює з додатним напрямом осікут. Тоді.

Якщо точка по кривійнаближатиметься до точки, то координати точкинаближатимуться до координат точки, тобто

.

Звідси випливає, що коли точка , то. З іншого боку, якщо, то за неперервністю функціїмаємо:, тобтоі при цьому. Таким чином

.

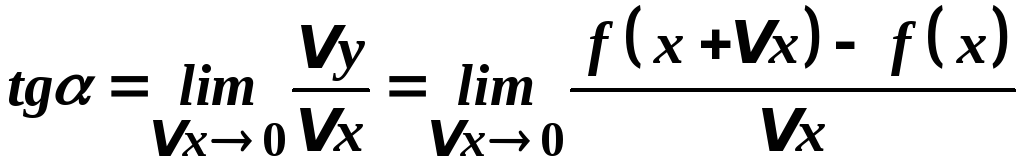Розглянуті задачі різні за своїм змістом, але вони відрізняються одним і тим способом, якщо в кожній з цих задач незалежну змінну позначити через , а залежну змінну – через, то для знаходження розв'язку кожної із них потрібно знаходити границю відношення приросту функції до приросту аргументу, за умови, що приріст аргументу прямує до нуля, тобто

.