5.4. Екстремальна властивість центра ваги

Для точок на площині їх центром ваги будемо називати таку точку, що.

Така точка існує і єдина. Справді, для довільної точки з рівності

випливає, що точки таспівпадають. Відмітимо, що центром ваги для трьох вершин трикутника буде точка перетину його медіан.

Описане геометричне означення узгоджується з фізичним, якщо в точках розмістити маси однакової величини.

Центр ваги має наступну екстремальну властивість. Для будь-якої точки виконується нерівність

.

Справді, використовуючи скалярний добуток, отримуємо

.

Задача 5.4.1. Довести нерівність, де- сторони довільного трикутника,- радіус описаного навколо нього кола.

Розв’язання. Нехай- центр описаного кола,- точка перетину медіан. Тоді згідно з доведеним

,

що доводить задану нерівність.

5.5. Дослідження екстремальних властивостей

Задача 5.5.1. У прямокутний трикутник з гострим кутом та прямим кутом вписано правильний трикутник так, що його вершини лежать на різних сторонах даного трикутника. При якій умові сторона правильного трикутника буде найменшою?

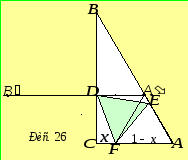
Розв’язання. Нехай – правильний трикутник, вписаний у даний трикутник (рис. 26). Вважатимемо . Тоді. Точку можна розглядати, як результат повороту точки навколо точкина кут проти годинникової стрілки. Тоді точку можна одержати внаслідок перетину відрізківта, де- це образ відрізкапри повороті на проти годинникової стрілки навколо центра повороту . Оскільки кут , то точка. Очевидно, що – правильний і . Знайдемо висоту у :. Із прямокутного трикутника сторона вписаного трикутника дорівнює . Розглянемо функцію. Вона набуває свого найменшого значення при =.

Отже, якщо , тобто, то вписаний правильний трикутник буде шуканий.

Задача 5.5.2. Всередині трикутника знайти точку, для якої сума квадратів відстаней від неї до сторін трикутника мінімальна.

Р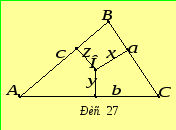озв’язання. Нехай відстані від точки до сторін ,будуть відповідно (рис. 27). Тоді

,

де - площа даного трикутника. Сума квадратів відстаней від точки до сторін трикутника буде дорівнювати. В силу нерівності Коші - Буняковського виконується співвідношення

,

причому знак рівності виконується при умові . Одержуємо, що

.

Права частина є сталим числом. Тому ліва частина прийматиме найменше значення, коли виконується знак рівності, тобто при умові . Із цих співвідношень та рівності остаточно дістаємо

.

Задача 5.5.3.Дано дві паралельні прямі та точкаміж ними. Побудувати прямокутний трикутникз вершиною прямого кута в точціта вершинами на заданих паралельних прямих, площа якого мінімальна.

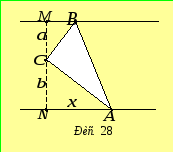
Розв’язання.Проведемо через точкуперпендикуляр до паралельних прямих (рис. 28). Нехай. Трикутникиіподібні. Томуабо, звідки. Оскількиі, то. Отже, площабуде найменшою, коли найменшою буде сума. Добутокє сталим числом, тому сумабуде найменшою при, тобто при. Але якщо, то. Тепер трикутниклегко будується.

Задача 5.5.4.Знайти найкоротший відрізок, який ділить рівносторонній трикутник із стороноюна дві рівновеликі фігури.

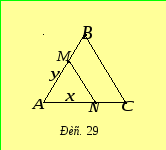
Розв’язання. Нехай трикутникрівносторонній із стороною. Позначимо шуканий відрізок. Нехай,(рис. 29). Тоді площа. Оскільки площа всього трикутника дорівнює, то з умови отримуємо, щоабо. За теоремою косинусівабо. Очевидно, що відрізокбуде найменшим, коли найменшим буде значення виразу. Добуток обох доданків є сталим і, тому найменше значення суми буде при, тобто при. При цьому значенніі.