3.3. Застосування тригонометрії

При перетворенні виразів з метою їхнього спрощення іноді використовуються тригонометричні заміни. Такими можуть бути:

абопри наявності в умові виразу;

або, якщо в умові фігурують блокиабоз перспективою виконати заміни відповідноабо;

,, якщо наявний вираз;

при наявності виразу;

,,,, якщо потрібно перетворювати вираз;

при наявності виразівта.

Наведемо приклади задач, в яких використовуються подібні ідеї.

Задача 3.3.1. Числазадовольняють умови,. Довести, що.

Доведення.Оскільки,, то існують такі числа, що,. Отримуємо

.

Задача 3.3.2. Довести, що приівиконується нерівність

.

Доведення. Враховуючи те, що, можна ввести заміну. Тоді

Задача 3.3.3. Дійсні числаналежать відрізку, причому сума кубів цих чисел дорівнює 0. Довести, що.

Доведення. Нехай. Маємо

.

Задача 3.3.4. Довести, що при довільних дійсних числахвиконується нерівність

.

Доведення.Враховуючи довільність у виборі чисел, виконаємо заміни,,,. Тоді

.

Звідси випливає справедливість твердження, яке ми доводимо.

Задача 3.3.5. Для довільних дійсних чисел(крім випадку, колитаодночасно дорівнюють 0) довести нерівність

.

Доведення. Перейдемо до полярних координат, ввівши заміну,(). Дістаємо

.

Тепер оцінимо значення виразу . Маємо

, де.

Таким чином, вираз може змінюватися у межах віддо, що доводить задану нерівність.

Задача 3.3.6.Довести, що із довільних 13 чисел завжди можна вибрати два числата, для яких виконуватиметься нерівність.

Доведення. Позначимо черезчисла, про які іде мова в умові задачі. Нехай, де. Розіб’ємо проміжокна 12 рівних частин. Тоді знайдуться принаймні два кутитатакі, що. Звідси. Нехай,. Тоді. Доведення рівностіне викликає затруднень. Маємо .

Задача 3.3.7.Довести, що для кутів А, В, С довільного трикутника виконується нерівність . Встановити, коли досягається рівність.

Доведення. Для зручності нерівність попередньо помножимо на 2. Маємо

.

Тепер отримуємо

,

звідки випливає, що . Рівність досягається, колиі. Тому маємо, щоі, звідки, тобто трикутник повинен бути рівностороннім.

Розділ 4. Застосування деяких геометричних співвідношень до доведення нерівностей

4.1. Геометричний спосіб доведення нерівностей між середніми квадратичним, арифметичним, геометричним та гармонічним

Задача 4.1.1.Довести нерівності між середнім квадратичним, арифметичним, геометричним та гармонічним у випадку двох чисел, тобто той факт, що для довільнихвиконуються співвідношення

.

Розв’язання.Наведемо один із можливих геометричних способів доведення.

Розглянемо трапецію з основами та. Позначимо черезсередню лінію трапеції. Тодібуде середнім арифметичним чиселта.

Відрізком , паралельним до основ трапеції, поділимо її на дві рівновеликі трапеції (рис. 9), площу кожної з яких позначимо через. Продовжимо бічні сторони трапеції до перетину та позначимо площу трикутника, що утворився поза трапецією через. З подібності трьох трикутників, що утворилися, випливає пропорція. Звідси отримаємо рівністьабо. Таким чином, відрізокє середнім квадратичним відрізківта. Середня лінія трапеції розташована вище від відрізка, оскільки ділить трапецію на дві, з яких верхня має меншу площу, ніж нижня. Тому вона має меншу довжину, ніж відрізок. Цим самим показано, що, тобто, що середнє арифметичне не більше середнього квадратичного.

Нехай відрізок паралельний до основ трапеції і ділить її на дві подібні трапеції. З подібності випливає пропорція, тобтоє середнім геометричним чиселта.

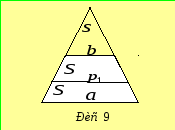
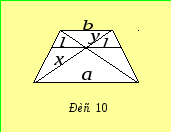
Нехай відрізокпаралельний до основ трапеції і проходить через точку перетину її діагоналей. З подібності трикутників легко встановити, що частини цього відрізка від точки перетину діагоналей трапеції до її бічних сторін рівні. Позначимо їх довжини через, а частини довільної з діагоналей з кінцями у точці перетину діагоналей та у вершинах трапеції черезта(рис. 10).

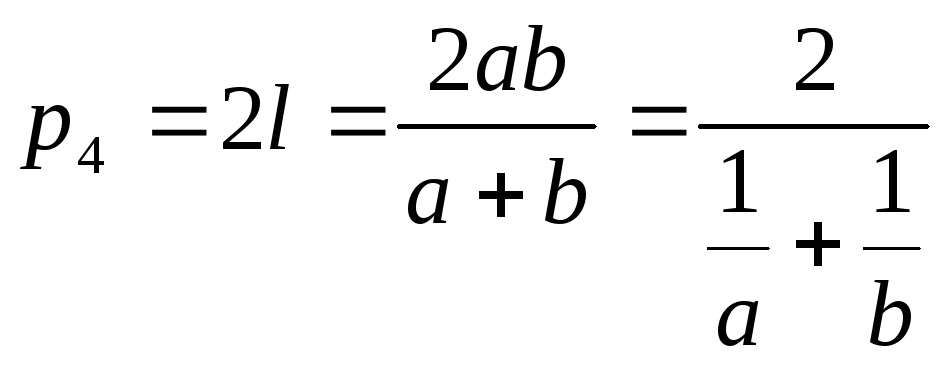З подібності трикутників отримуємо співвідношення та, звідки. Томуі, тобтоє середнім гармонічним чиселта.

Тепер чисто геометрично легко показати, що відрізки задовольняють нерівності, що завершує доведення алгебраїчних нерівностей.

Наведемо ще одне геометричне доведення нерівності Коші.

Задача 4.1.2.Довести, що, де.

Р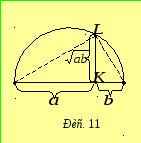озв’язання.Нехай задані дрізкита. Побудуємо на відрізку, як на діаметрі, коло і у спільній для відрізків точціпроведемо перпендикулярдо перетину з колом (рис. 11). З подібності прямокутних трикутників випливає, що, звідки. Очевидно, що цей відрізок не може перевищувати довжину радіуса кола, який дорівнює. Тому.