85

Розділ 3. Застосування методів аналітичної геометрії, векторної алгебри, тригонометрії

3.1. Застосування методів аналітичної геометрії

Традиційними для аналітичної геометрії є застосування ідеї координатного методу. Відповідно до нього вводиться певна система координат. Після цього кожній парі значень змінних можна поставити у відповідність точку з такими ж координатами, лінійному рівнянню відповідатиме на координатній площині пряма. Алгебраїчний виразтепер можна трактувати, як відстань між двома точками з координатамита.

Взагалі кажучи, певні алгебраїчні співвідношення тепер можна розглядати з точки зору співвідношень між геометричними фігурами та величинами. При доведенні нерівностей це робить його геометрично наглядним та створює ширші можливості для пошуку нових ідей доведень. Наведемо приклади.

Задача 3.1.1. Знайти найменше значення виразу

.

Розв’язання.Запишемо даний вираз у видіта введемо в розгляд точки,,,(рис. 4). Маємо

,

,.

Тепер, користуючись нерівністю трикутника, можна стверджувати, що і для довільних значеньтавиконується співвідношення

.

Отже, найменше значення виразу дорівнює 5. Рівність буде виконуватися для всіх точок відрізка.

Задача 3.1.2. Довести, що для довільних значень змінних виконується нерівність.

Доведення.Розглянемо на координатній площині точки,,. Використавши формулу відстані між двома точками, отримуємо,,. Посилання на нерівність трикутника завершує доведення. Знак рівності виконується, наприклад, при.

Задача 3.1.3. Знайти найбільше та найменше значення виразу, якщо.

Розв’язання.Введемо в розгляд точки,та. Тоді виразможна трактувати, як суму відрізківта. Графіком залежностіє ромб(рис. 5). Умову задачі на мові геометрії тепер можна сформулювати наступним чином: знайти найбільше та найменше значення суми відрізківта, якщо точканалежить ромбу. Розглянемо. Маємо(рівність досягається, коли точкаспівпадає з точкою). Оскількиі, то(рівність досягається, коли точкаспівпадає з точкою).

Таким чином, найбільше значення виразу буде 7, а найменше значення 3.

Задача 3.1.4. Знайти найменше значення виразу, якщо.

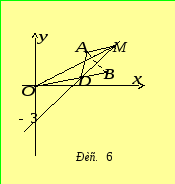
Розв’язання. На координатній площині розглянемо точки,і точку, що належить прямій. Задача полягає в тому, щоб на вказаній прямій знайти таке положення точки, при якому сума відрізківбуде мінімальною. Нехай точкасиметрична точцівідносно прямої. Тоді точка, в якій перетнуться пряміта пряма, буде шуканою (рис. 6).

Справді, у цьому випадку для довільної відмінної відточки. Таким чином, знаходимо точкута довжину відрізка.

Отже, найменше значення виразу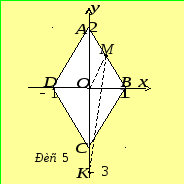буде.

Задача 3.1.5. Довести нерівність

.

Розв’язання.Для доведення достатньо ввести в розгляд точки, та, зауваживши, що

,,

,

скористатися нерівністю трикутника.

Аналогічно до попередньої вправи доводиться нерівність

.

3.2. Застосування методів векторної алгебри

Ідея застосування векторів при доведенні нерівностей ґрунтується на таких простих геометричних міркуваннях.

Розглянемо два вектори . Очевидно, що виконується нерівність, або в координатному виді

.

Нехай виконується векторна рівність . Переходячи до довжин векторів, отримуємо, що(нерівність трикутника). Оскільки, то з одержаної нерівності випливає, що

.

В обох випадках кількість координат векторів може бути взята довільною і ми отримаємо більш загальні, ніж наведені, співвідношення. Рівність в них досягається при умові колінеарності векторів.

Наведемо приклади.

Задача 3.2.1.Для довільних невід’ємних чисел, таких, щовиконується нерівність. Довести.

Доведення. Введемо в розгляд вектори. Оскільки,і, то, використовуючи нерівність, отримуємо

.

Рівність буде виконуватися при умові, коли , тобто прита довільних невід’ємнихтаких, що.

Задача 3.2.2. Якщо, то. Довести.

Доведення. Розглянемо векторита. Оскільки,, то, застосувавши до них співвідношення, отримуємо нерівність, яку потрібно довести. Рівність буде виконуватися при умові пропорційності координат векторів, тобто, коли. З даних пропорцій випливає, що.

Задача 3.2.3.Довести, що привиконується нерівність

.

Доведення. Тепер у розгляд доцільно ввести векторита . Використавши нерівність, отримуємо

,

звідки випливає нерівність, яку ми доводимо. Зауважимо, що дану нерівність ми уже доводили, користуючись синтетичним методом (приклад 1.2.7).

Задача 3.2.4.Довести, що для довільнихвиконується нерівність

.

Розв’язання. Введемо в розгляд векторита. Тепер, використовуючи нерівність, отримуємо співвідношення, що доводиться.

Задача 3.2.5.Довести, що для довільнихвиконується нерівність

.

Доведення.Введемо в розгляд векторита. Використовуючи нерівність для скалярного добутку у виді, отримуємо потрібне співвідношення.

Задача 3.2.6. Довести, що нерівністьвиконується при всіх значеннях, для яких визначена її ліва частина.

Доведення. Розглянемо векторита. Очевидно, що ліва частина нерівності являє собою скалярний добуток цих векторів і не перевищує добутку їх довжин, тобто виконується співвідношення

.

Знак рівності можливий тільки у випадку пропорційності координат векторів, тобто тільки тоді, коли . Оскільки система даних рівнянь несумісна, то нерівність строга.

Задача 3.2.7. Довести, що якщо числазадовольняють умову, то виконується нерівність.

Доведення. Розглянемо векторита. Оскільки ліва частина нерівності являє собою скалярний добуток цих векторів і не перевищує добутку їх довжин, то виконується співвідношення

.

Знак рівності виконується при .

Задача 3.2.8. Довести, що , якщо.

Доведення. Розглянемо векторита. Очевидно, щоі. Використавши нерівність, отримуємо, що. Рівність буде виконуватися при.

Задача 3.2.9. Розв’язати рівняння.

Розв’язання. Введемо в розгляд векторита. Тепер оцінимо ліву частину рівняння:. Оскільки рівність виконується тільки при умові колінеарності векторів, то корені потрібно шукати серед розв’язків рівняння. Перетворивши його до виду, отримуємо рівнянняз єдиним дійсним коренем. Знайдене значення є коренем заданого рівняння.

Задача 3.2.10. Числатакі, що. Знайти найбільше та найменше значення виразу.

Розв’язання. Очевидно, що для оцінки виразукоординати векторів потрібно вибрати так, щоб модуль одного з них дорівнював. Тому введемо в розгляд векторита. Тепер маємо.

Отже, .

Ті значення змінних, при яких досягаються найбільше та найменше значення можна знайти, використовуючи умову колінеарності векторів таі рівність, тобто розв’язавши систему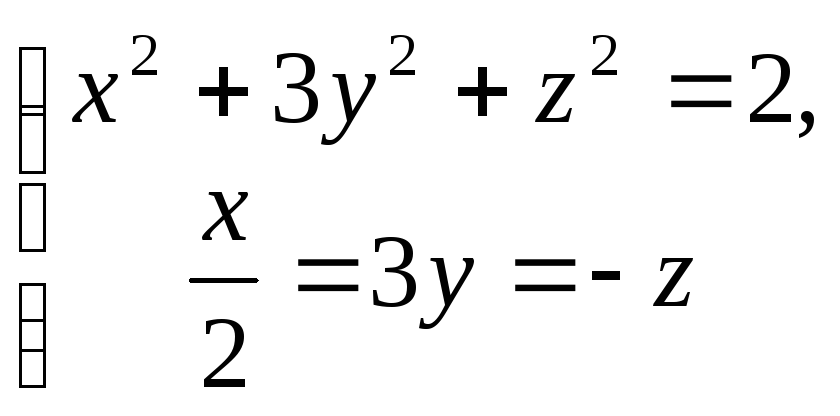. Отримуємо два розв’язки, на яких заданий вираз досягає екстремальних значень.

Задача 3.2.11. Довести, що для довільнихвиконується нерівність.

Доведення. Рівність одиниці модуля вектораможе бути підказкою для вибору координат векторів. Отже, нехай,. Тоді дістаємо

.

Знак рівності отримуємо, наприклад, при .

Задача 3.2.12. Довести нерівність, де- кути трикутника.

Доведення. Виберемо на сторонах трикутника одиничні векториітак, як показано на рисунку 7. Із очевидного співвідношеннядістаємо

звідки випливає нерівність, яку ми доводимо. Знак рівності виконується для рівностороннього трикутника.

Задача 3.2.13. Довести, що якщо- кути трикутника, то виконується нерівність.

Доведення. Нехай коло з центром у точціта радіусомописане навколо заданого трикутника (рис. 8). Тоді. Із очевидного співвідношенняотримуємо

,

звідки випливає нерівність, яку ми доводимо. Знак рівності виконується для рівностороннього трикутника.

Задача 3.2.14. Довести нерівність.

Доведення. Розглянемо векторита. Тоді

.

Знову введемо в розгляд нові вектори та. Дістаємо

,

що завершує доведення. Рівність виконується тільки при умові .