
f1_8_2008
.pdf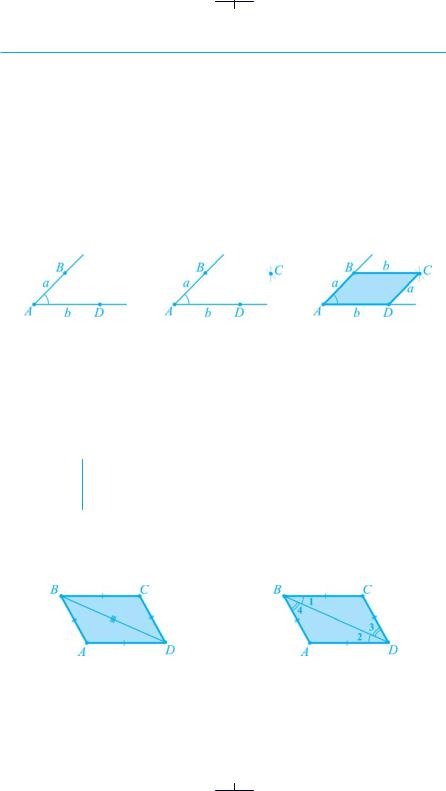
2.2. Ознаки паралелограма |
31 |
4.Оскільки кути BCA і DAC — внутрішні різносторонні при прямих BC
йAD та січній AC, то з їх рівності випливає паралельність прямих BC і AD.
5.Отже, чотирикутник ABCD — паралелограм за означенням (AB||CD — за умовою, BC||AD — за доведеним). ●
2.Ознака паралелограма за рівністю протилежних сторін.
Побудуємо кут A, менший від розгорнутого, й відкладемо на його сторонах відрізки АB = a; AD = b (рис. 31 а).
Опишемо коло з центром у точці В, радіус якого дорівнює b, і коло з центром у точці D, радіус якого дорівнює a (рис. 31 б). С — точка перетин кіл.
а |
б |
в |
Рис. 31
Сполучаємо точку C з точками B і D (рис. 31 в). Отримуємо чотирикутник, у якого протилежні сторони рівні. Можна припустити, що в цього чотирикутника протилежні сторони паралельні, тобто що чотирикутник є паралелограмом.
Теорема
Якщо в чотирикутнику протилежні сторони рівні, то він є паралелограмом.
● Доведення. Нехай ABCD — довільний чотирикутник, у якого протилежні сторони рівні: AB = CD і BC = AD. Доведемо, що чотирикутник ABCD — паралелограм.
а |
б |
Рис. 32
32 |
§2. Паралелограм |
|
1. |
Проведемо одну з діагоналей чотирикутника, наприклад, |
BD |
(рис. 32 а). Вона поділяє його на два трикутники BAD і DCB, рівні за трьома |
||
сторонами. |
|
|
2. |
Для зручності як 1–4 позначимо кути, на які діагональ BD поділяє |
|
кути B і D чотирикутника (рис. 32 б). З рівності трикутників випливає, |
що |
|
1 = 2, 3 = 4. |
|
|
3.Оскільки кути 1 і 2 — внутрішні різносторонні при прямих AD і BC та січній BD, то з їх рівності випливає, що AD||BC (за ознакою паралельності прямих).
Оскільки кути 3 і 4 — внутрішні різносторонні при прямих AB і CD та січній BD, то з їх рівності випливає, що AB||CD.
4.Отже, у чотирикутнику ABCD протилежні сторони паралельні, а отже, за означенням, він є паралелограмом. Теорему доведено. ●
3.Ознака паралелограма за діагоналями.
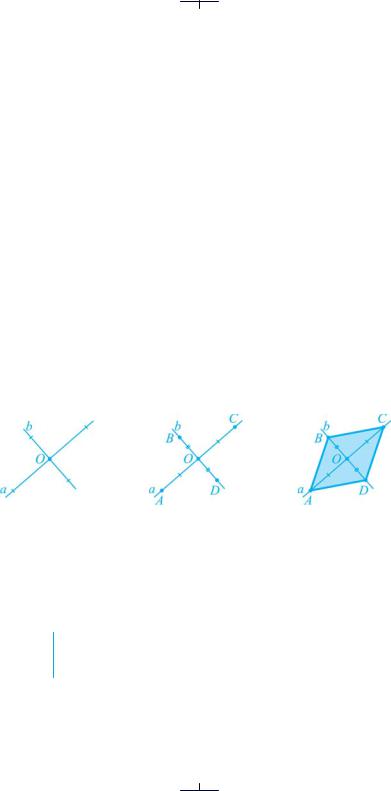
Проведемо прямі a і b, які перетинаються в точці О (рис. 33 а). Відкладемо на прямій a рівні відрізки OA й OC, а на прямій b — рівні відрізки OB й OD (рис. 33 б).
а |
б |
в |
Рис. 33
Послідовно сполучимо відрізками точки A, B, C і D (рис. 33 в).
Можна припустити, що утворений чотирикутник ABCD є паралелогра-
мом.
Теорема
Якщо діагоналі чотирикутника в точці перетину діляться навпіл, то він є паралелограмом.
● Доведення. Нехай ABCD — довільний опуклий чотирикутник, у якого діагоналі перетинаються в точці О й кожну з них точка перетину ділить навпіл: ОA = ОC, OB = OD (рис. 34 а). Доведемо, що ABCD — паралелограм.
2.2. Ознаки паралелограма |
33 |
а |
б |
в |
Рис. 34
1.Трикутники АОВ і СОD рівні за двома сторонами та кутом між ними (AO = OC, BO = OD — за умовою, AOB = COD як вертикальні).
2.З рівності трикутників AOB і COD випливає рівність кутів BAO і DCO (рис. 34 б). Оскільки ці кути внутрішні різносторонні при прямих AB і CD та січній AC, то прямі AB й CD — паралельні.
3.Аналогічно з рівності трикутників AOD і COB випливає паралельність АD і BC.
4.Таким чином, у чотирикутнику ABCD протилежні сторони паралельні (AB||CD і AD||BC). Отже, ABCD паралелограм (за означенням). ●
1.Які умови повинні виконуватися для чотирикутника, щоб він був паралелограмом: а) за означенням; б) за парою сторін; в) за рівними сторонами; г) за діагоналями?
2.Використавши горизонтальні лінії зошита, накреслити такий чотирикутник, щоб у нього дві сторони були паралельні та дорівнювали по 3 см. Встановити вид чотирикутника. Відповідь обґрунтувати.
3.Побудувати такий чотирикутник, у якого дві протилежні сторони дорівнюють по 4 см, а дві інші — по 3 см. Встановити вид чотирикутника.
4.Позначити довільну точку O. Використавши ознаку паралелограма, побудувати паралелограм, у якого діагоналі перетинаються в точці O.
34 |
§2. Паралелограм |
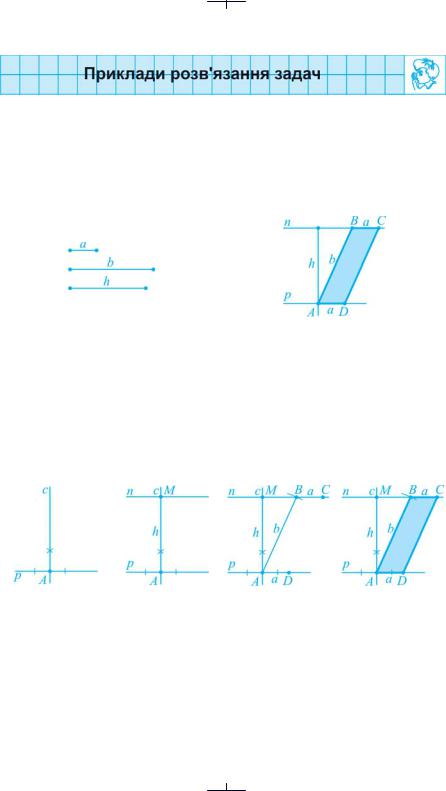
Задача 1. Побудувати паралелограм за двома сторонами і висотою, проведеною до меншої з них (рис. 35).
Розв’язання
● Дано: a і b — сторони паралелограма ABCD, h — його висота. Побудувати: паралелограм ABCD.
Рис. 35 |
Рис. 36 |
Аналіз
Нехай АВСD — побудований паралелограм (рис. 36). Очевидно, що спочатку можна побудувати паралельні прямі n і p, відстань між якими дорівнює h, а потім на одній з них відкласти меншу сторону AD. Після цього побудуємо точку В, яка повинна належати прямій n і бути віддаленою від точки А на відстань b.
а |
б |
в |
г |
Рис. 37
Побудова
1.Проводимо довільну пряму р, позначаємо на ній точку А й через неї проводимо пряму с, перпендикулярну до прямої р (рис. 37 а).
2.Відкладаємо на прямій с відрізок АМ = h і проводимо через точку М пряму п, перпендикулярну до прямої с (рис. 37 б).
2.2. Ознаки паралелограма |
35 |
3.Будуємо коло з центром у точці А, радіус якого дорівнює b. Точку перетину кола з прямою п позначаємо як В. В одну півплощину відносно прямої АВ відкладаємо на прямій р відрізок AD = а, а на прямій п — відрізок
ВС = а (рис. 37 в).
4.Сполучаємо відрізком точки А і В та C і D (рис. 37 г).
Утворений чотирикутник ABCD є шуканим паралелограмом (ознака за парою протилежних сторін). ●
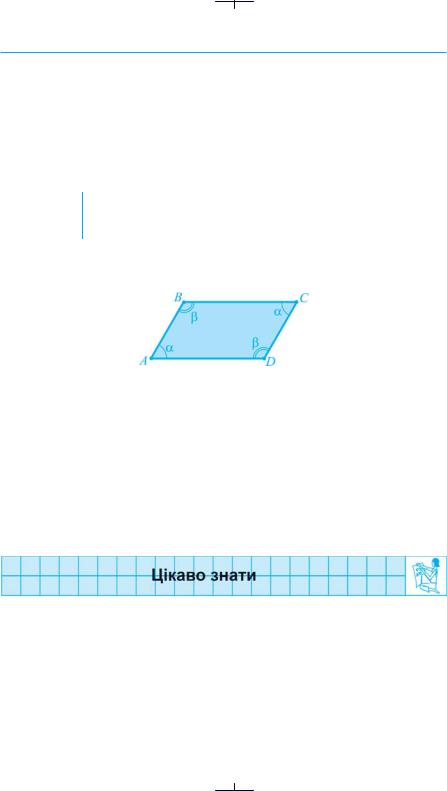
Задача- Довести: якщо в чотирикутнику протилежні кути рівні, то він теорема є паралелограмом.
●Доведення. Нехай АBCD — паралелограм, у якого А = С = α і В =
=D = β (рис. 38).
Рис. 38
За теоремою про суму кутів чотирикутника маємо: α + β + α + β = 360º; 2(α + β) = 360º; α + β = 180º. Отже, А + В = 180º і А + D = 180º. Кути А і В — внутрішні односторонні при прямих AD і ВС та січній АВ. ОскількиА + В = 180º, то за ознакою паралельності, AD||ВС. Кути А й D — внутрішні односторонні при прямих АВ і СD та січній АD. Оскільки А + + D = 180º, то АВ||CD. Таким чином, у чотирикутника ABCD АВ||CD і ВС||АD. Отже, ABCD — паралелограм. ●
Термін паралелограм походить від поєднання грецьких слів паралелос — «той, що йде поряд», і грамма — «риска, лінія».
Поняття паралелограма та деякі його властивості були відомі вже Піфагору та його учням (VI ст. до н. е.).
Вважають, що термін паралелограм був уведений Евклідом (ІІІ ст. до н. е.). У його «Началах» доведена теорема про поділ паралелограма на рівні трикутники та рівність його протилежних сторін і кутів. Однак він не згадує про властивість точки перетину діагоналей паралелограма.
36 |
§2. Паралелограм |
Повна теорія паралелограмів була розроблена в кінці середніх віків і з’явилась у підручниках лише у XVII ст. Виклад властивостей паралелограма містить підручник «Курс математики. Геометрія» професора математики Харківського університету Тимофія Федоровича Осиповського, виданий у 1804 році. У своєму підручнику він зазначає, що паралелограми та чотирикутники можна досліджувати шляхом розгляду властивостей тих трикутників, на які вони можуть бути поділені діагоналями.
Властивості й ознаки паралелограма описує в «Підручнику з елементарної геометрії» Михайло Васильович Остроградський. Наведемо його доведення ознаки паралелограма за кутами: «Якщо в чотирикутнику протилежні кути рівні, то чотирикутник є паралелограмом».
«Так, позначимо буквами а і b кути, що прилягають до однієї зі сторін чотирикутника. Два інші кути, відповідно протилежні першим, будуть теж а й b. Отже, сума всіх чотирьох кутів — 2а + 2b. А оскільки вона дорівнює 4d (d — прямий кут), то a + b = 2d, тобто сума кутів, що прилягають до довільно взятої сторони, дорівнює двом прямим. З цього випливає паралельність, а отже, і рівність протилежних сторін».
66.У чотирикутнику ABCD A + B = 180° і A + D = 180°. Довести, що чотирикутник ABCD є паралелограмом.
67.У чотирикутнику MNOK KMO = NOM і MОK = NМО. Довести, що чотирикутник MNOK є паралелограмом.
68.У чотирикутнику FSPT діагоналі перетинаються в точці Q й утворюють відрізки SQ = 8 см, TQ = 0,8 дм, FQ = 120 мм, FP = 24 см. Чи є цей чотирикутник паралелограмом?
69.У чотирикутнику MNKP протилежні сторони MN і KP рівні. Діагональ MK утворює з цими сторонами рівні кути. Довести, що MNKP — паралелограм.
70.У паралелограмі ABCD на сторонах АВ і CD відкладено рівні відрізки АМ і CK. Довести, що MBKD — паралелограм.
71.Накреслити дві паралельні прямі, відстань між якими дорівнює 3 см. Побудувати паралелограм, у якого дві сторони є відрізками цих прямих і дорівнюють по 3 см, а один з кутів дорівнює 50°.
72.Побудувати паралелограм, у якого дві сторони дорівнюють 3 см і 4 см, а один з кутів — 40°.
2.2. Ознаки паралелограма |
37 |
73.Побудувати паралелограм, у якого діагоналі дорівнюють 6 см і 8 см, а кут між ними — 30°.
74.Побудувати паралелограм, у якого сторони дорівнюють 4 см і 5 см, а одна з діагоналей — 6 см.
75.У паралелограмі ABCD на діагоналі BD відкладено рівні відрізки BM і DK, менші від половини діагоналі BD. Довести, що чотирикутник AMCK є паралелограмом.
76.У паралелограмі ABCD на сторонах AB й CD відповідно відкладені рівні відрізки AF і CЕ. Довести, що діагональ BD ділить відрізок EF навпіл.
77.У паралелограмі ABCD на сторонах АВ й CD взято точки F і P так, щоADF = CBP (рис. 39). Довести, що чотирикутник FBPD — паралелограм.
Рис. 39
78.FBPD — паралелограм (рис. 39), ADF = CBP. Довести, що чотирикутник АВСD — паралелограм.
79.На рисунку 40 АВСD — паралелограм. Точка О ділить діагональ BD навпіл. Довести, що KBMD — паралелограм.
Рис. 40
80.Побудувати паралелограм за стороною та двома діагоналями.
38 |
§2. Паралелограм |
81.Побудувати паралелограм за стороною, висотою, проведеною до неї, й діагоналлю.
82.Побудувати паралелограм за стороною, висотою, проведеною до неї, і гострим кутом.
83.Побудувати паралелограм за двома сторонами та висотою, проведеною до більшої з них.
 Довести, що середини сторін паралелограма є вершинами нового паралелограма.
Довести, що середини сторін паралелограма є вершинами нового паралелограма.
Вказівка. Використати рівність трикутників.
85.З вершин тупих кутів B й D паралелограма ABCD на діагональ AC опущено перпендикуляри BO й DK. Довести, що чотирикутник BKDO є паралелограмом.
86.На сторонах BC й AD паралелограма ABCD відповідно позначено точки M і K, такі, що BM = KD. Довести, що діагональ AC ділить відрізок MK навпіл.
87.На діагоналі АС паралелограма АВСD взято точки М і Р так, що АМ = СР, а на діагоналі BD точки N і D так, що BN = DQ (рис. 41). Довести, що MNPQ — паралелограм.
Рис. 41
88.У паралелограмі ABCD — бісектриси кутів В й D перетинають діагональ АС у точках M і K. Довести, що точки В, М, D і K — вершини паралелограма.
89.Довести, що два трикутники рівні, якщо дві сторони та медіана, проведена до третьої сторони одного трикутника, відповідно дорівнюють двом сторонам і медіані, проведеній до третьої сторони іншого трикутника. Вказівка. Добудувати трикутники до паралелограмів.

2.2. Ознаки паралелограма |
39 |
90.Побудувати трикутник, якщо відомі дві його сторони а й b та медіана mc, проведена до третьої сторони.
91.Довести: якщо через точку перетину діагоналей паралелограма провести дві прямі й з’єднати послідовно точки перетину цих прямих зі сторонами паралелограма, то одержаний чотирикутник буде паралелограмом.
92.Побудувати паралелограм за гострим кутом і двома висотами.
93.Побудувати паралелограм за двома діагоналями та висотою.
94.Побудувати паралелограм за стороною та двома висотами.
Середній рівень
1.Яку фігуру називають паралелограмом?
2.Яка властивість у паралелограмі:
а) протилежних сторін; |
б) протилежних кутів; |
в) сусідніх кутів; |
г) діагоналей? |
3.Яка ознака паралелограма:
а) за парою протилежних сторін; б) за рівними сторонами; в) за діагоналями?
Достатній рівень
4.Сформулювати й довести теорему-властивість: а) протилежних сторін і кутів паралелограма; б) діагоналей паралелограма.
5.Сформулювати і довести ознаку паралелограма: а) за парою протилежних сторін; б) за протилежними сторонами; в) за діагоналями.
Високий рівень
6.Сформулюватийдовестиознаку паралелограмазапротилежнимикутами.
40 |
Завдання для самоконтролю |
Початковий рівень
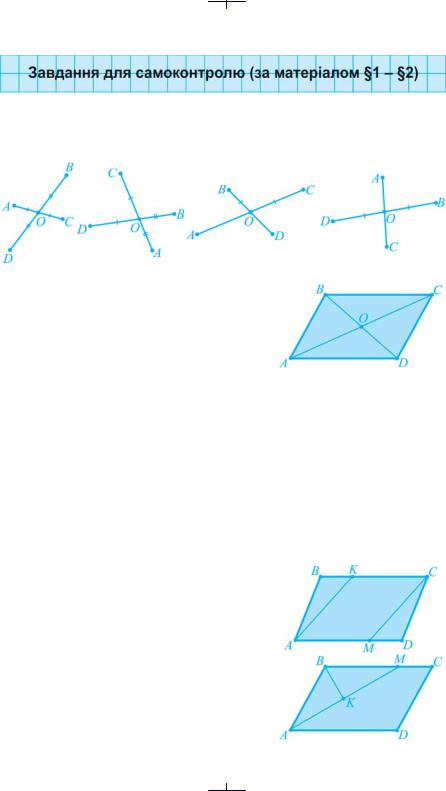
1.На якому з рисунків точки А, В, С і D є вершинами паралелограма
АВСD?
а |
б |
в |
г |
2.О — точка перетину діагоналей паралелограма АВСD. Який з відрізків дорівнює
відрізку ОА?
а) ОС; б) OD;
3.Якщо кут А паралелограма АВСD дорівнює 35°, то кут В дорівнює...
а) 55°; |
б) 35°; |
в) 145°; |
г) 180°. |
Середній рівень
4.Знайти невідомі сторони паралелограма, якщо його периметр дорівнює 18 см, а одна зі сторін — 6 см.
5.О — точка перетину діагоналей паралелограма АВСD. Знайти периметр трикутника COD, якщо АВ = 7 см, АС = 12 см, BD = 8 см.
6.Знайти кути паралелограма, якщо сума двох з них дорівнює 72°.
Достатній рівень
7. АВСD — паралелограм, у якому
AD = 15 см, AM = 10 см, BK = 5 см. Дове-
сти, що AKCM — паралелограм.
8.AM — бісектриса кута А паралелограма ABCD, точка K — середина відрізка АМ. Довести, що BK AM.
