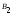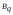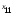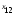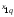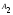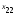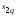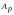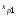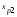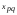2.2. Двухфакторный дисперсионный анализ

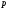Обобщением однофакторного дисперсионного анализа является многофакторный анализ, когда учитывается одновременно несколько факторов. Рассмотрим воздействие на признак двух независимых факторови, имеющихи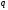фиксированных уровней соответственно. Для всех возможных сочетаний уровней проведено одно измерение, т.е. всего измерялось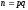значений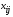признака, где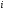- индекс уровня фактора,- индекс уровня фактора.

Результаты наблюдений представляют в виде таблицы 2.6.

Т а б л и ц а 2.6

Матрица экспериментов

Уровень фактора	Уровни фактора
			…
			…
			…
…	…	…	…	…
			…

Расчетные формулы средних значений признака :

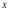• на каждом уровне фактора

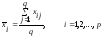. (2.12)

• на каждом уровне фактора

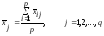. (2.13)

• по всем наблюдениям

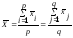. (2.14)

Расчетные формулы дисперсий признака :

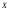• на каждом уровне фактора

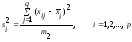. (2.15)

• на каждом уровне фактора

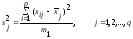. (2.16)

Число степеней свободы:

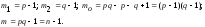
Суммы, характеризующие влияние факторов на признак 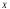, и общая сумма квадратов:

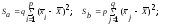
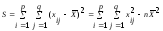; (2.17)

,

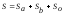где 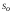- остаточная сумма квадратов отклонений. Тогда

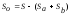. (2.18)

Дисперсии:

Статистическая значимость влияния на признак факторов проверяется сравнением расчетных значений- критерия

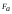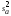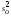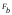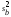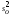=/;=/(2.19)

с критическими значениями критерия 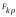при заданных значениях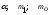и.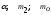

Если 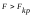, то влияние факторов значимо (существенно). В этом случае дисперсионный анализ может быть продолжен проверкой значимости средних значений групп фактораили фактора. Для этого достаточно визуально сравнить средние значения и дисперсии признака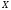по столбцам или строкам.

Пример 2.2 [1]. При спектрографическом исследовании были проведены испытания с целью проверки влияния различных электродов (фактор ) и фотопластинок (фактор ) на признак, характеризующий интенсивность света. Результаты испытаний и дисперсионного анализа приведены в таблице 2.7, расчетные формулы – в таблице 2.9

Т а б л и ц а 2.7

Дисперсионный анализ влияния электродов и

фотопластинок

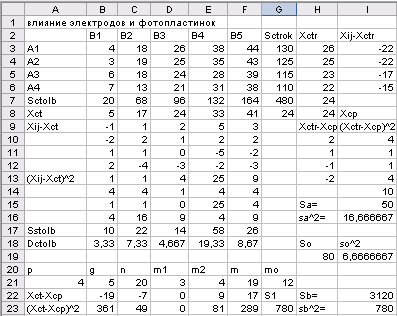
Продолжение таблицы 2.7

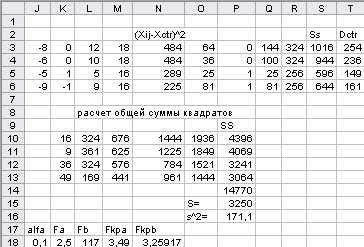
Сводка дисперсионного анализа, полученная с помощью инструмента Двухфакторный дисперсионный анализ без повторений пакета анализа, приведена в таблице 2.8.

Т а б л и ц а 2.8

Сводка дисперсионного анализа

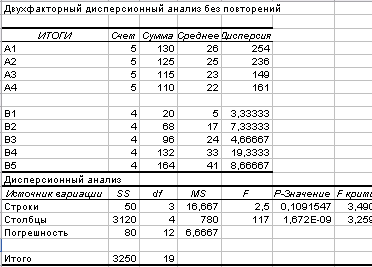
Как следует из дисперсионного анализа для:

• электродов , т.е. гипотеза о том, что электроды не влияют на исследуемый признак, подтверждается;

• фотопластинок , т.е. фотопластинки существенно влияют на исследуемый признак.

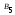Результаты дисперсионного анализа таблиц 2.7 и 2.8 совпадают. Анализ средних значений и дисперсий по столбцам (фактор - фотопластинки) показывает, что уровеньобеспечивает высокое среднее значение признака и относительно невысокое рассеивание возможных значений признака около среднего значения.

Диалоговое окно инструмента Двухфакторный дисперсионный анализ без повторений представлено на рис. 2.2.

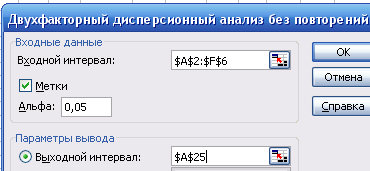
Рис. 2.2. Диалоговое окно Двухфакторный