Завдання для самоконтролю

1. Як виявляється закономірність розподілу?

2. Назвіть особливості частотних характеристик розподілу.

3. Чому саме середню розглядають як типовий рівень ознаки в сукупності? Як співвідноситься середня з іншими характеристиками центра розподілу?

4. Середня величина ознаки у двох сукупностях однакова. Чи може бути різною варіація цієї ознаки?

5. Терміни корисного використання нематеріальних активів фірми, захищених патентами, ліцензіями тощо, на кінець року становили:

Таблиця 5.4

Терміни використання нематеріальних активів фірми

Термін використання, років	1	2	3	4	5	6	Разом
У % до загальної суми нематеріальних активів	2,6	10,2	39,2	40,0	6,8	1,2		100

Визначить ряд кумулятивних часток, медіану і моду терміну корисного використання нематеріальних активів фірми.

6. Кредитні ставки комерційних банків під короткострокові позики становили:

Таблиця 5.5

Кредитні ставки комерційних банків

Кредитна ставка, %	Суми наданих позик, млн. грн.
	І квартал	ІІ квартал
До 10	1	5
10 — 20	4	11
20 — 30	9	8
30 і більше	6	6
Разом	20	30

За кожний квартал визначить середню кредитну ставку та середнє лінійне відхилення. Як змінилися середній рівень і варіація кредитної ставки?

7. Прибутковість активів комерційних банків на початок року становила в середньому 15% при дисперсії 36, на кінець року — 10% при дисперсії 25. Оцініть відносну варіацію прибутковості активів на початок і кінець року, зробіть висновок про напрямок зміни середньої і варіації.

8. Розподіл агропідприємств за рівнем урожайності кукурудзи (ц/га) на зрошувальних землях характеризується даними:

Таблиця 5.6

Розподіл агропідприємств за рівнем урожайності кукурудзи

Режим іригації	Середній рівень	Модальне значення	Середнє квадратичне відхилення
1	60	57,0	12
2	75	70,5	9

Порівняйте варіацію та асиметрію розподілу агропідприємств за рівнем урожайності кукурудзи.

9. Квадратичний коефіцієнт варіації витрат домогосподарств на харчування становить 79%. Чи можна вважати однорідною сукупність домогосподарств за цією ознакою?

6. Методи аналізу взаємозв’язків

Розрізняють два типи зв’язків — функціональні та стохас­тичні. У разі функціонального зв’язку кожному значенню фактора х відповідає одне або кілька чітко визначених значень у.

На відміну від функціональних, стохастичні зв’язки неоднозначні. Стохастичні зв’язки виявляються як узгодженість варіації двох чи більше ознак. У ланці зв’язку «х  у» кожному значенню ознаки х відповідає певна множина значень ознаки у, які утворюють так званий умовний розподіл.

Важливою характеристикою кореляційного зв’язку є лінія регресії — емпірична в моделі аналітичного групування і теоретична в моделі регресійного аналізу. Емпірична лінія регресії представлена груповими середніми результативної ознаки , кожна з яких належить до відповідного інтервалу значень групувального фактора х_j. Теоретична лінія регресії описується певною функцією яку називають рівнянням регресії, а Y — теоретичним рівнем результативної ознаки.

На відміну від емпіричної, теоретична лінія регресії неперервна. Так, уважають, що маса дорослої людини в кілограмах має бути на 100 одиниць менша за її зріст у сантиметрах. Співвідношення між масою і зростом можна записати у вигляді рівняння: , де у — маса; х — зріст.

Безперечно, така форма зв’язку між масою та зростом людини надто спрощена. Насправді збільшення маси не жорстко пропорційне до збільшення зросту. Люди одного зросту мають різну масу, проте в середньому зі збільшенням зросту маса зростає. Для точнішого відображення зв’язку між цими ознаками в рівняння слід увести другий параметр, який був би коефіцієнтом пропорційності при х, тобто Y = – 100 + bx.

Рівняння регресії в такому вигляді описує числове співвідношення варіації ознак х і у в середньому. Коефіцієнт пропорційності при цьому відіграє визначальну роль. Він показує, на скільки одиниць у середньому змінюється у зі зміною х на одиницю. У разі прямого зв’язку b — величина додатна, у разі оберненого — від’ємна.

Різні явища по-різному реагують на зміну факторів. Для того щоб відобразити характерні особливості зв’язку конкретних явищ, статистика використовує різні за функціональним видом регресійні рівняння. Якщо зі зміною фактора х результат у змінюється більш-менш рівномірно, такий зв’язок описується лінійною функцією Y = a + bx. Коли йдеться про нерівномірне співвідношення варіацій взаємозв’язаних ознак (наприклад, ко­ли прирости значень у зі зміною х прискорені чи сповільнені або напрям зв’язку змінюється), застосовують нелінійні регресії, зокрема:

степеневу ;

гіперболічну ;

параболічну тощо.

Вибір та обґрунтування функціонального виду регресії ґрунтується на теоретичному аналізі суті зв’язку. Нехай вивчається зв’язок між урожайністю та кількістю опадів. Надто мала і надто велика кількість опадів спричинюють зниження врожайності, максимальний її рівень можливий за умови оптимальної кількості опадів, тобто зі збільшенням факторної ознаки (опади) урожайність спершу зростає, а потім зменшується. Залежність такого роду описується параболою Y = a + bx + cx².

Вивчаючи зв’язок між собівартістю у та обсягом продукції х, використовують рівняння гіперболи , де а — пропорційні витрати на одиницю продукції, b — постійні витрати на весь випуск.

Параметр b (коефіцієнт регресії) — величина іменована, має розмірність результативної ознаки і розглядається як ефект впливу x на y. Параметр a — вільний член рівняння регресії, це значення y при x = 0. Якщо межі варіації x не містять нуля, то цей параметр має лише розрахункове значення.

Математично доведено, що значення параметрів a та b, при яких мінімізується сума квадратів відхилень, визначаються із системи нормальних рівнянь:

,

.

Розв’язавши цю систему, знаходимо такі значення параметрів:

,

.

Розглянемо порядок обчислення параметрів лінійної регресії на прикладі зв’язку між урожайністю зернових і кількістю внесених добрив (у центнерах діючої поживної речовини — д. р.). Значення взаємозв’язаних ознак та необхідні для розрахунку параметрів величини наведено в табл. 7.3.

= 12; = 224;= 342,8;= 18,68;

= 12 : 8 = 1,5; = 224 : 8 = 28.

Таблиця 6.1

ДО РОЗРАХУНКУ ПАРАМЕТРІВ ЛІНІЙНОЇ РЕГРЕСІЇ, ТЕОРЕТИЧНИХ РІВНІВ І ЗАЛИШКОВИХ ВЕЛИЧИН

Номер господар-ства	Кількість внесених добрив х, д. р	Урожайність зернових у, ц/га	ху	х2	Y	y – Y	(y – Y)2
1	1,1	23	25,3	1,21	24	–1	1
2	1,4	25	35,0	1,96	27	–2	4
3	1,2	26	31,2	1,44	25	1	1
4	2,0	33	66,0	4,00	33	0	0
5	1,5	27	40,5	2,25	28	–1	1
6	1,3	2,8	36,4	1,69	26	2	4
7	1,8	30	54,0	3,24	31	–1	1
8	1,7	32	54,4	2,89	30	2	4
Разом	12,0	224	342,8	18,68	224		16

Користуючись цими величинами, визначаємо:

(ц/га);

.

Отже, рівняння регресії має вигляд

,

Рівняння регресії відбиває закон зв’язку між х і у не для окремих елементів сукупності, а для сукупності в цілому; закон, який абстрагує вплив інших факторів, виходить з принципу «за інших однакових умов». За цих умов очікувана врожайність зернових при внесенні добрив у обсязі 1,1 ц д. р. на 1 га становить Y = 13 + 10  1,1 = 24 (ц/га).

Відповідно загальна дисперсія врожайності

,

залишкова дисперсія

.

У невеликих за обсягом сукупностях коефіцієнт регресії схильний до випадкових коливань. Тому слід перевірити його істотність. Коли зв’язок лінійний, істотність коефіцієнта регресії перевіряють за допомогою t-критерію (Стьюдента), статистична характеристика відношенням коефіцієнта регресії b до власної стандартної похибки

тобто .

Стандартна похибка коефіцієнта регресії залежить від варіації факторної ознаки залишкової дисперсіїі числа ступенів свободи, де m — кількість параметрів рівняння регресії:

.

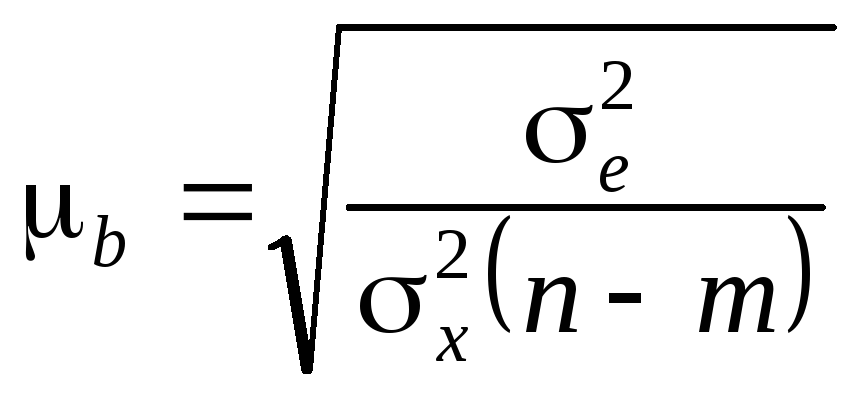Для лінійної функції m = 2. За даними табл. 6.1 маємо:

.

Звідси (ц/га), а, що перевищує критичне значення двостороннього t-критерію. Гіпотеза про випадковий характер коефіцієнта регресії відхиляється, а отже, з імовірністю 0,95 вплив кількості внесених добрив на врожайність зернових визнається істотним.

Для коефіцієнта регресії, як і для будь-якої іншої випадкової величини, визначаються довірчі межі . У нашому прикладі довірчі межі коефіцієнта регресії з імовірністю 0,95 (t = 2,45) становлять.

Важливою характеристикою регресійної моделі є відносний ефект впливу фактора х на результат у — коефіцієнт еластичності:

.

Він показує, на скільки процентів у середньому змінюється результат у зі зміною фактора х на 1%. У нашому прикладі тобто збільшення кількості внесених добрив на 1% спричинює приріст урожайності зернових у середньому на 0,8%.