4. Интервальные оценки коэффициентов линейного уравнения регрессии

Cтатистикииимеют распределение Стьюдента с числом степеней свободы.

Для определения –годоверительного интервала по требуемому уровню значимостии числу степеней свободыопределяется критическое значение, удовлетворяющее условию:

.

Подставляя каждую из формул для и, получим:

,.

После преобразования получим:

,

.

Выражения в скобках определяют доверительные интервалы теоретических коэффициентов регрессии и, которые будут приемлемыми с надежностьюпри найденных оценкахи.

5. Доверительные интервалы для зависимой переменной

Одной из задач эконометрического моделирования является прогнозирование значений зависимой переменной при определенных значениях независимой переменной.

Пусть построено уравнение регрессии , на основе которого необходимо предсказать условное математическое ожиданиепеременнойYпри. Значениеявляется оценкой. Возникает вопрос:как сильно может отклониться модельное значение от соответствующего условного математического ожидания?

Используя формулы для ииз п.2, получим:

.

Следовательно, СВ является линейной комбинацией нормальных СВ, значит и сама имеет нормальное распределение.

,

.

.

Получили:

.

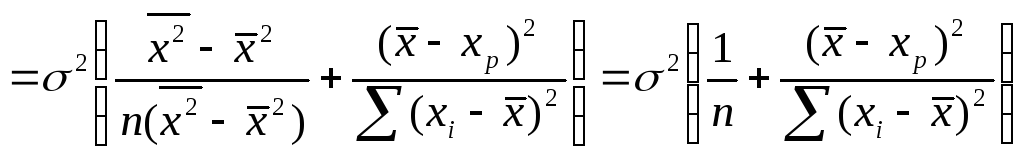Подставив вместо ее несмещенную оценку, получим выборочную исправленную дисперсию рассматриваемой СВ:

.

Тогда СВ имеет распределение Стьюдента с числом степеней свободы. Следовательно, по требуемому уровню значимостии числу степеней свободыможно определить критическую точку, которая удовлетворяет условию. Подставляя вместоt значение, имеем:

.

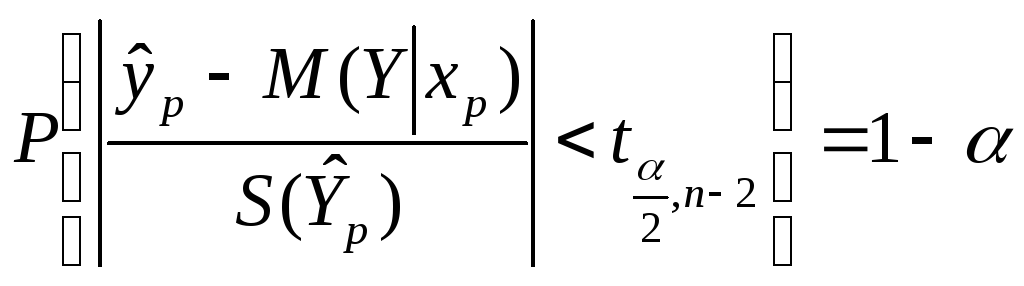После преобразования получим:

,

,

.

Таким образом, доверительный интервал для условного математического ожидания имеет вид:

.

6. Проверка общего качества уравнения регрессии

Суммарной мерой общего качества уравнения регрессии, т.е. соответствия уравнения регрессии статистическим данным, является коэффициент детерминации , который рассчитывается по формуле:

.

Выясним смысл коэффициента детерминации.

Реальные значения отличаются от модельныхна:

,.

Последнее соотношение можно переписать в виде:

,,

где – отклонениеi–й наблюдаемой точки от среднего значения,– отклонениеi–й точки на линии регрессии от среднего значения,– отклонениеi–й наблюдаемой точки от модельного значения.

Возведем обе части в квадрат и просуммируем по объему выборки:

.

Доказывается, что , тогда справедливо следующее соотношение:

,

где –общая (полная) сумма квадратов,являющаяся мерой общего разброса переменнойYотносительно,–объясненная сумма квадратов, которая является мерой разброса, объяснимого с помощью регрессии,–остаточная (необъясненная) сумма квадратов, являющаяся мерой не объясненного уравнением регрессии разброса точек вокруг линии регрессии.

Разделив на левую его часть, получим:

.

Вводя обозначение , получим исходное соотношение.

Коэффициент детерминацииопределяет долю разброса зависимой переменной, объяснимую регрессией, т.е величинапоказывает, какая часть вариации зависимой переменной объясняется независимой переменной.

Дробь определяет долю разброса зависимой переменной, не объясненную регрессией.

Из проведенных рассуждений следует, что в общем случае справедливо соотношение . Чем ближе коэффициент детерминации к 1, тем лучше качество построенной регрессии.

.

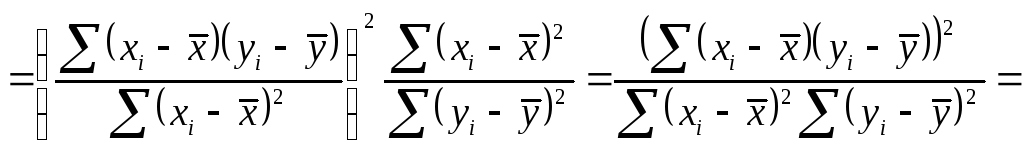
Как видно, коэффициент детерминации равен квадрату коэффициента корреляции. Следовательно, его можно рассчитывать по формуле:

.

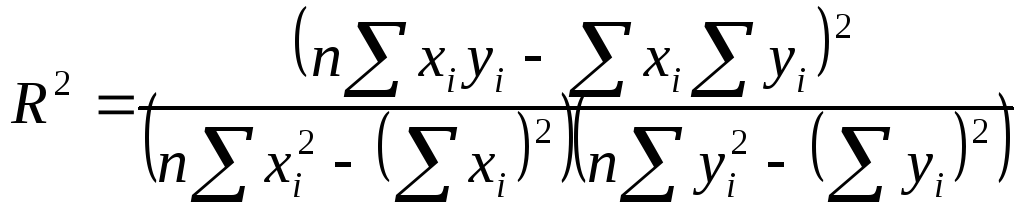Для оценки качества построенной регрессии используется также средняя ошибка аппроксимации:

.

Качество построенной регрессии считается хорошим, если .