Проверка качества уравнения регрессии

1. Предпосылки метода наименьших квадратов

Регрессионный анализ позволяет определить оценки коэффициентов регрессии. Но, являясь лишь оценками, они не позволяют сделать вывод:

• насколько близки оценки коэффициентов 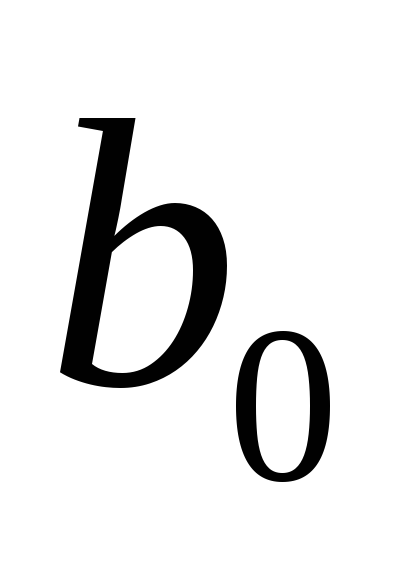ик своим теоретическим коэффициентами;

• насколько надежны найденные оценки;

• как близко оцененное значение к условному математическому ожиданию;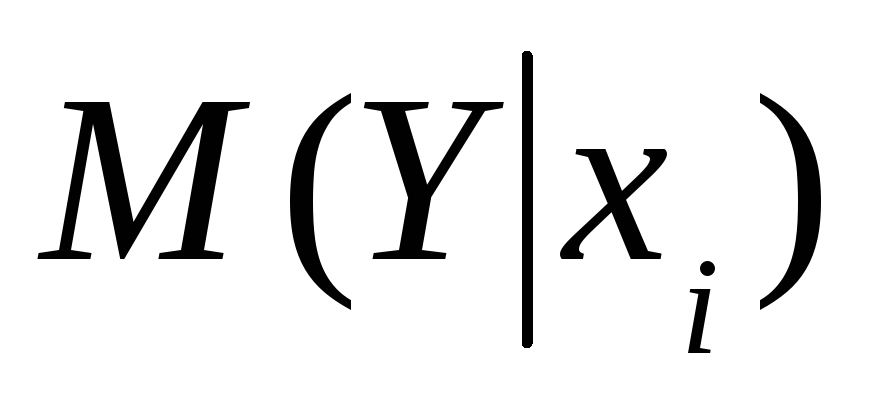

• насколько точно эмпирическое уравнение регрессии соответствует уравнению для всей генеральной совокупности.

Из соотношения ,, следует, что значениязависят от значенийи случайных отклонений. Следовательно, пока не будет определенности в вероятностном поведении, мы не сможем быть уверенными в качестве оценок.

Рассмотрим модель парной линейной регрессии: .

Пусть на основе выборки из nнаблюдений оценивается регрессия:.

Покажем, что оценки коэффициентов регрессии иявляются СВ, которые зависят от случайного членав уравнении регрессии.

Выше показано, что коэффициент регрессии можно вычислить по формуле:

.

Видно, что коэффициент является случайным, т.к. значение выборочной ковариациизависит от значений переменныхXиY. Если переменнаяX– это экзогенный фактор, значения которого известны, то значения переменнойYзависят от случайной составляющей . Теоретически коэффициентможно разложить на неслучайную и случайную составляющие:

.

Здесь – это постоянная величина (истинное значение коэффициента регрессии), а– это случайная величина. Аналогичный результат можно получить и для.

Мы показали, что оценки коэффициентов регрессии, а следовательно, и качество построенной регрессии, зависят от свойств случайной составляющей.

Для получения по МНК наилучших оценок необходимо выполнение предпосылок Гаусса–Маркова относительно случайного отклонения:

1. Математическое ожидание случайного отклонения для всех наблюдений равно нулю: . Данное условие означает, что случайное отклонение «в среднем» не оказывает влияния на зависимую переменную. Выполнимость влечет выполнимость ,.

2. Дисперсия случайных отклонений постоянна для любых наблюдений i и j: .Выполнимость данной предпосылки называетсягомоскедастичностью(постоянством дисперсии отклонений), а невыполнимость –гетероскедастичностью(непостоянством дисперсии отклонений). Т.к. , то данную предпосылку можно переписать в виде: .

3. Случайные отклонения иявляются независимыми друг от друга для, т.е. не коррелированны:

Выполнение данной предпосылки говорит об отсутствии автокорреляции. С учетом предпосылки 1 последнее соотношение можно записать в виде:

,если .

4. Случайные отклонения являются независимыми от экзогенных переменных. Данное условие предполагает выполнимость следующего соотношения:

.

5. Модель является линейной относительно параметров.

Теорема (Гаусса–Маркова).Если предпосылки 1–5 выполняются, то оценки, полученные МНК, обладают следующими свойствами:

1. Оценки являются несмещенными, т.е.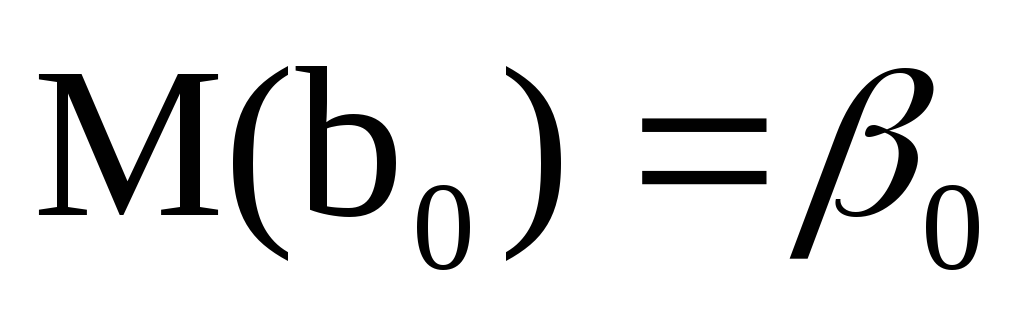и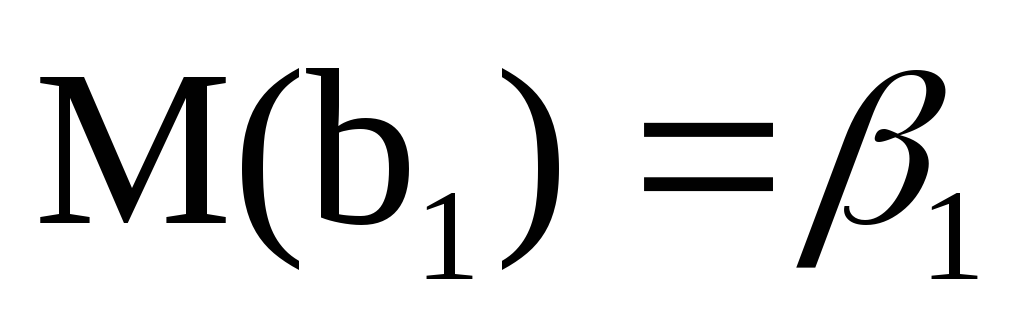. Это вытекает из того, что 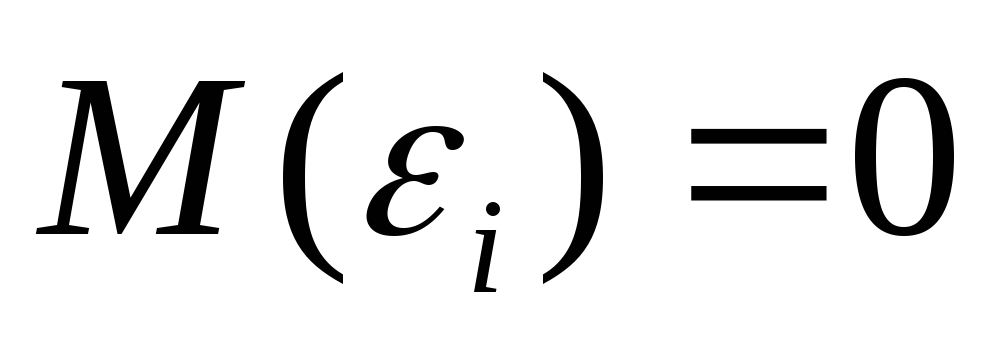, и говорит об отсутствии систематической ошибки в определении положения линии регрессии.

2. Оценки являются состоятельными, т.е. дисперсия оценок параметров при возрастании числа наблюдений стремиться к нулю: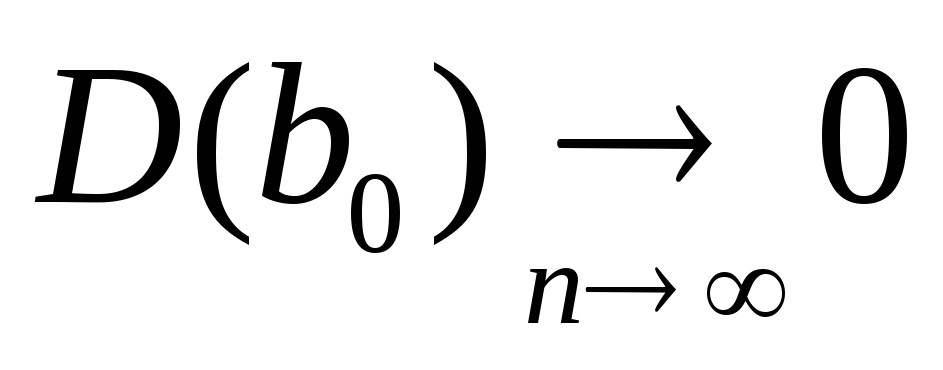и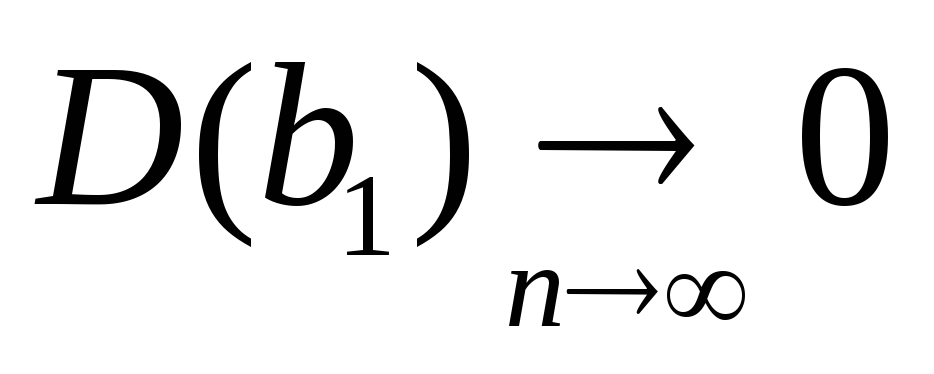. Другими словами, при увеличении объема выборки надежность оценок увеличивается, т.е.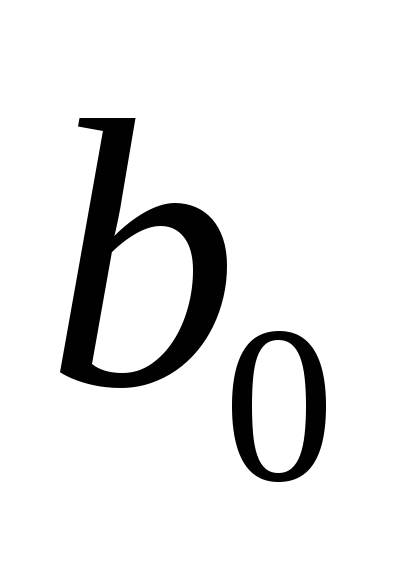близко к, а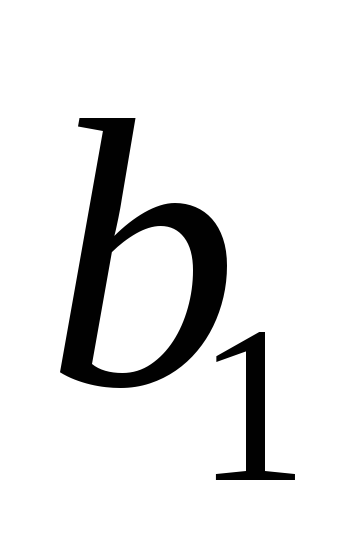близко к.

3. Оценки являются эффективными, т.е. они имеют наименьшую дисперсию по сравнению с любыми другими оценками данных параметров.

В англоязычной литературе такие оценки называются BLUE (Best Linear Unbiased Estimators) – наилучшие линейные несмещенные оценки.

Наряду с выполнимостью указанных предпосылок делаются предположения, что экзогенные переменные не являются СВ, случайные отклонения имеют нормальное распределение, число наблюдений существенно больше числа независимых переменных, отсутствуют ошибки спецификации.