34. Точки разрыва и их классификация.

Рассм. функцию y=f(x), определ. на интервале (a,b), кроме быть может, тчк. х₀ x₀ наз. точкой разрыва данной ф-ции, если в ней ф-ция определена, но не явл. непрерыв. или не определ. в этой точке.

Если х₀ - точка разрыва ф-ции f(x) и сущ. конечные пределы ,то она наз.точкой разрыва первого рода.

Если х₀ - точка разрыва и по крайней мере один из пределовявл. бесконечным или не сущ., тоназ. точкой разрыва второго рода.

35. Производная ф-ции. Гео. И эк. Смысл.

Производной ф-ции y=f(x) в тч. Х₀ наз. предел отношения приращения этой ф-ции к приращению аргумента , когда последнее стремится к нулю.

Формулавыражаетгеометрический смысл производной: производная от данной ф. в данной точке = tg угла наклона касательной графика ф-ции в этой тчк. Производительность труда есть производная объема продукции по времени. Рассмотрим некоторые понятия, иллюстрирующие экономический смысл производной. Пусть y(x) – ф-ция, характеризующая, например, издержки производства, где x - количество выпускаемой продукции. Тогда отношение описывает средние издержки, приходящиеся на одно изделие. Средняя величина обозначается Ay или Af (от английского "average".) Среднее приращение, средний прирост, средняя скорость изменения определяется отношением. Производнаявыражает предельные издержки производства. Величину Mf(x) = y' наз. мгновенным приростом или мгновенной скоростью изменения y. Аналогично можно определ. предельную выручку, предельный доход, предельную полезность и др. предельные величины.

Правила дифференцирования: 1.Производная сум.(разности) двух дифференц-ых ф-ций =сумме(разности) производных этих ф-ций

2.Производная произведения двух диффиренц-ых ф-ций = произведению первой ф-ции на роизводную второй + произведение второй ф-ции на производную первой:

3.Производная частного двух дифференц-ых ф-ций определ. формулой:

где

36. Произв. Сложной и обр. Ф-ции. Табл. Производных.

Производная сложной ф.:Если и-дифференцируемые ф. своих аргументов, то производная сложной ф.сущ. и равна произведению производной этой ф-ции по промежуточному аргументу на производную промежуточного по независимой переменной, т.е.

, .

Производная обратной ф.:Еслиy=f(x) и - взимно-обратые дифференцируемые ф-ции и,тоДействительно,т.к.,то

Таблица производной

,,,,,,

,,

,,,

,

37. Диф-л функции, его геометр. смысл. Приближенные выч-ия с пом. Диф-ла.

Рассм. Ф-ию y=f(x), имеющую произв. в каждой точке ее обл. опр-я. Диф-лом ф-и y=f(x) наз. произведение произв-й этой ф-и на приращение независ. переменной х Диф-л независ. переем-й равен приращению этой переменной, поэтому диф-л ф-и равен произведению ее производной на диф-л незав. перем-ой.Геометр. смысл: диф-л ф-и равен приращению ординаты касательной к граф. Данной ф-и, когда аргумент получает приращение дельта х.

Бесконечно малое приращение ф-и эквивал. диф-лу этой ф-и при всех знач. незав. перем-ой, для кот-х произв-я ф-и конечна и отлична от нуля.f(x+дельтах)прибл.=f(x)+f’(x)*дельтаХ. Эта ф-ла позволяет вычислять прибл. знач-е ф-и, соотв-ее приращ-му знач. аргумента, если известно ее знач. в этой т. и знач. производной в этой т., когда приращение арг-та достаточно мало.

38.Теорема Ферма и Роля. Теорема Ферма: Если функция f(x) определена на интер(а, b) и в некот.точке x₀ этого интервала имеет наибольшее или наименьшее значение, тогда если в точке х₀ существует производная, то она равна нулю.

Теорема Роля: Если функция y=f(x) непрерывна на отрезке [a, b] и дифференцируема внутри этого отрезка, причем f(a)=f(b), то существует по крайней мере одна точка x=c, принадлежащей отрезку (a, b), такая, что f’(c)=0 (касательная // OX)

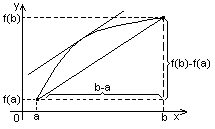
39. Теорема Лагранжа: Если функция y=f(x) непрерывна на отрезке [a, b] и дифференцируема внутри этого отрезка, то существует по крайней мере одна точка с, принадлежащая отрезку (а, b), для которой справедлива формула: f(b)-f(a)/(b-a)=f”(c).Эта формула наз. Формулой конечных приращений Лагранжа.

40. Правило Лопиталя. Исп. при вычис.пределов для раскрытия неопредел.();().Теорема Лопиталя: Если ф-и у=f(х) и у=ф(х) удовлетв. услов. теор. Коши в нек.окрестн. х=,стремят. к 0() при хи сущ.lim ,то сущlimи эти пределы равны.Пр.Лопиталя справедливо и при =.

Пример: lim sinx/x=lim (sinx)’/x’=lim cosx/1=1.