69.Понятие степенного ряда .Область сходимости степенного ряда

Ряд вида а₀ + а₁ х + а₂ х² + … а_n хⁿ + … = (1) называется степенным рядом,

а – некоторые числа, х – переменная .

Коэффициентами степенного ряда называются числа а₀ , а₁ , … , а_n

Пример:1+х+х² + …+ хⁿ + … = - степенной ряд, все его коэффициенты равны 1.

Областью сходимости степенного ряда называется множество всех значений переменной х , при которых соответствующий числовой ряд сходится. Степенной ряд в предыдущем примере является бесконечной суммой членов геометрической прогрессии со знаменателем х . Его частичная сумма S =. Эта сумма имеет конечный пределпри │х│< 1. Поэтому областью сходимости исходного ряда является интервал (-1; 1).

Теорема Абеля а)Если степенной ряд (1) сходится при некотором значении х=х₀≠0, то он сходится

Абсолютно при всех значениях х , таких что │х│< │х₀│

б)Если степенной ряд (1) расходится при х = х₁ , то он расходится при всех значениях х , таких что │х│> │х₁│.

70. Ряды Тейлора и Маклорена.

Пусть функция у = f (х) определена в некоторой окрестности точки х и имеет в ней производные до порядка n +1 включительно. Тогда для всякого х из этой окрестности справедливо равенство

f(x)= f(x₀ )+

Где с – некоторая точка из интервала (х, х )

Формулой Тейлора для функции f(x) в окрестности точки х называется многочлен

Р_n (х) = f(х₀ ) +

Остаточным членом формулы Тейлора называется последнее слагаемое в формуле Тейлора

R_n (x)= =f(x) – P_n (x)

Таким образом, многочлен Тейлора Р_n (х ) служит приближением функции f(х). Оценкой этого приближения служит остаточный член формулы Тейлора R_n (х ).

Формулой Маклорена для функции f(х) называется ее формула Тейлора при х₀ = 0:

f(x)= f(0) +

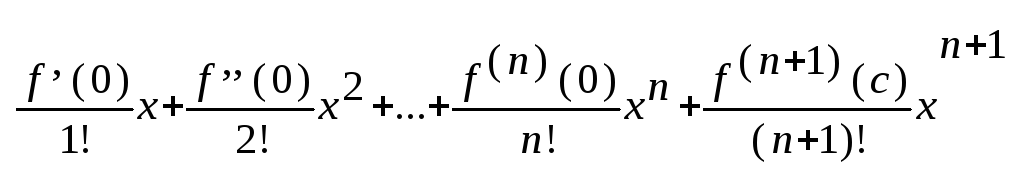
где с – некоторая точка из интервала (0, х).