3.2 Производная функции и ее применение к исследованию функции

Непрерывные функции

Определение 1. Функция называется непрерывной в точке, если она определена в этой точке и некоторой ее окрестности, существуети этот предел равен значению функции в этой точке, т.е.

.

Пример. Проверим непрерывность функции в произвольной точке:

.

Приращением переменной величины будем называть разность между двумя ее различными значениями. Пусть в начальный момент времени переменная величина имела значение , а затем в процессе своего изменения приняла какое-то значение, разностьназывается приращением этой переменной величины и обозначается.

Приращение функции соответствует взятому приращению аргумента.

Определение 2. Функция называется непрерывной в точке, если она определена в этой точке и некоторой ее окрестности, и бесконечно малому приращению аргументасоответствует бесконечно малое приращение функции.

Теорема 1. Если функции инепрерывны в точке, то их сумма, разность, произведениеи частноетакже непрерывны в этой точке.

Теорема 2. Если промежуточный аргумент непрерывен в точке, а заданная функциянепрерывна в точке, то сложная функциянепрерывна в точке.

Теорема 3. Всякая элементарная функция непрерывна в любой точке своей области определения.

Если в точке нарушены условия непрерывности функции, то в этой точке функция терпит разрыв; сама такая точка называется точкой разрыва.

Определение. Предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю, называется производной этой функции

.

Геометрический смысл производной

Производная в некоторой точкеравна угловому коэффициенту (тангенсу угла наклона) касательной, проведенной в точке касанияк графику функции.

Уравнение касательной имеет вид:

Физические интерпретации производной

Производная пути по времени = скорость движения .

Производная скорости по времени – ускорение движения .

Основные свойства производной

1. Постоянный множитель можно выносить за знак производной

2. Производная суммы нескольких функций равна сумме соответствующих производных слагаемых

Следствие. Производная разности есть разность производных

3. Производная произведения равна произведению производной первого множителя на второй плюс произведение производной второго множителя на первый

4. Дифференцирование частного:

5. Дифференцирование сложной функции

Производная сложной функции по независимой переменной равна производной заданной функции по промежуточному аргументу, умноженной на производную промежуточного аргумента по независимой переменной

Таблица производных

1. 9.

2. 10.

3. 11.

4. 12.

5. 13.

6. 14.

7. 15.

8. 16.

17.

Пример 1.

.

Пример 2.

.

Дифференциал функции

Дифференциалом функции в точкеназывается произведение производной функции, вычисленной в этой точке, на произвольное приращение аргумента

или

Приложения производной к исследованию функции

1. Признак возрастания и убывания функции

Теорема. Если функция дифференцируема во всех точках какого-то интервала и ее производнаяположительна в каждой точке, то функция возрастает на этом интервале. Если производнаяотрицательна, то функция убывает.

Пример. Исследовать функцию

, следовательно, функция возрастает при.

, следовательно, функция убывает при.

2. Признаки максимума и минимума.

Теорема (необходимый признак экстремума, признак Ферма). Если в точке экстремума имеет производную, то производная равна нулю.

Теорема (достаточный признак экстремума). Если при переходе через стационарную точку(движение слева направо) производная меняет знак с «+» на «–», то в- максимум, если же с «–» на «+», то- минимум.

В предыдущем примере, точка - точка максимума, точка- точка минимума.

3. Наибольшее и наименьшее значения функции на замкнутом интервале

Правило отыскания наибольших и наименьших значений:

1) находим производную исследуемой функции ;

2) определяем критические точки (решаем уравнение );

3) вычисляем значения функции в критических точках и концах интервала;

4) отбираем среди вычисленных значений самое большое и самое малое.

Пример. Найти наибольшее и наименьшее значение функции на отрезке [0,10].

1) ;

2) . Получили две критические точки (эти точки стационарные, разрывов унет);

3) составим таблицу значений в критических точках и в концах интервала:

	0	2	3	10
	-1

4) наибольшее значение достигается в правом конце интервала х=10, наименьшее значение (-1) в левом конце интервала х=0.

4. Выпуклость, вогнутость и точки перегиба кривой

Теорема. Если функция дважды дифференцируема во всех точках какого-то интервала и ее вторая производнаяположительна в каждой точке, то это является признаком выпуклости кривой. Если вторая производнаяотрицательна, то кривая вогнута.

Теорема (необходимый признак точки перегиба). Если - точка перегиба, то либо, либоне существует.

Теорема (достаточный признак точки перегиба). Если при переходе через точку вторая производная функциименяет знак, то- точка перегиба.

Пример.

;

Критическая точка:

для всех , следовательно, точек перегиба нет и кривая выпукла на всей числовой прямой.

5. Асимптоты

Прямая L называется асимптотой кривой, если расстояние от текущей точки М на кривой до прямой L становится бесконечно малой величиной, когда точка М неограниченно удаляется от начала координат (т.е. когда расстояние от М до начала координат ).

Вертикальные асимптоты могут образовываться только в точках бесконечного разрыва функции .

Пример. Определить вертикальные асимптоты функции .

Данная функция имеет точку разрыва х=2, ,. Таким образом, прямая х=2 – вертикальная асимптота.

Наклонные асимптоты

Пусть прямая L есть наклонная асимптота графика функции . Теперь точкаможет уходить на неограниченное расстояние от начала координат, лишь когда(надо, как правило, отдельно разбирать случаии). Уравнение наклонной асимптоты к кривойимеет вид:

.

Пример. Найти асимптоты линии

Знаменатель дроби обращается в нуль в точках . Проверим, будут ли вертикальные прямыеасимптотами:

.

Таким образом, прямые являются вертикальными асимптотами.

Найдем наклонные асимптоты:

=

.

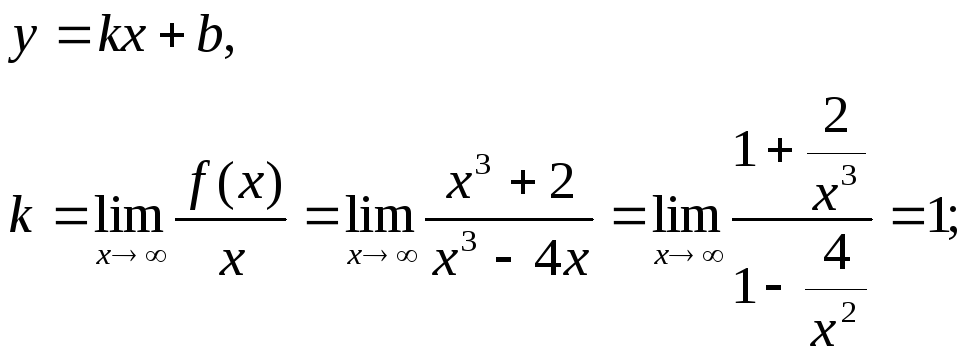
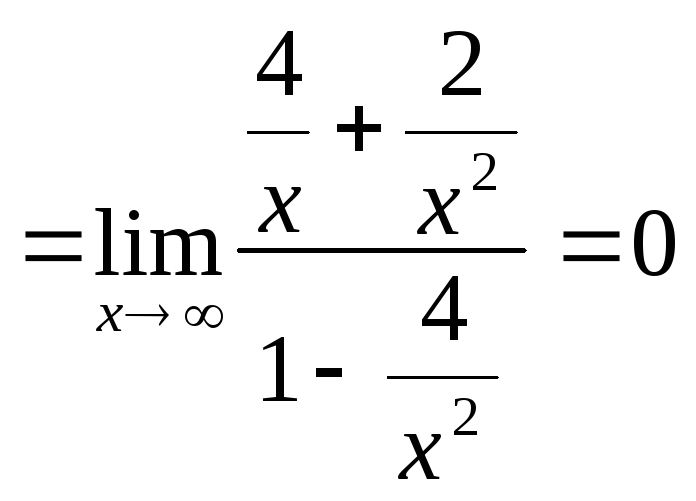Таким образом, наклонная асимптота .

Правило Лопиталя

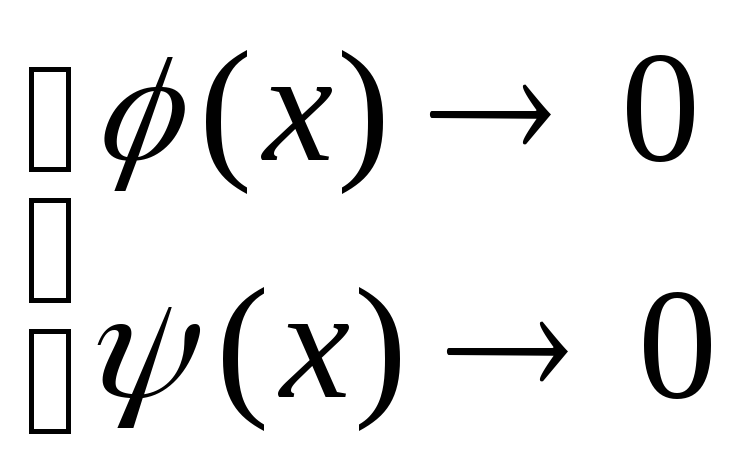Теорема (правило Лопиталя). Отыскивается приили, когда одновременноили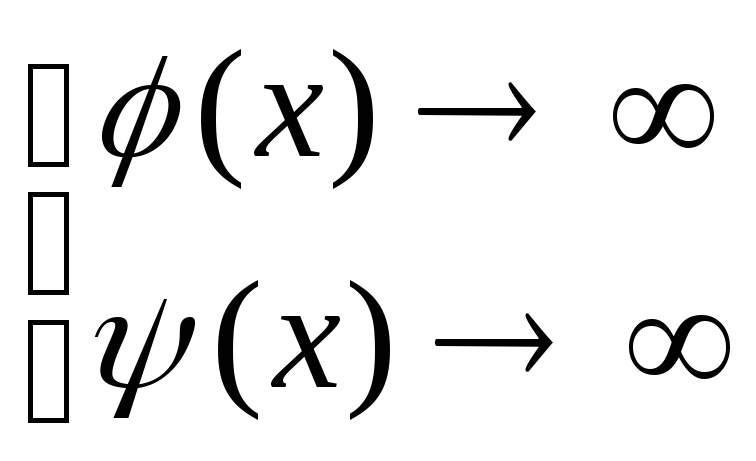(). Если существует предел (конечный или бесконечный) отношения производных, то существует и предел отношения функций и эти пределы равны:

.

Пример.

Общая схема исследования функции. Построение графика

1. Элементарное исследование: область определения; точки разрыва и интервалы непрерывности; точки пересечения графика с осями координат; симметрия графика: четность, нечетность; вертикальные и наклонные асимптоты.

2. Исследование на возрастание, убывание и точки экстремума с помощью производной функции.

3. Выпуклость, вогнутость и точки перегиба – с помощью второй производной.

4. Построение графика.