2.3 Аналитическая геометрия в пространстве

Плоскость в пространстве и ее уравнения

Пусть в пространстве введена прямоугольная система координатOXYZ. Рассмотрим в пространстве некоторую плоскость Q. Поверхности Q соответствует некоторое уравнение . Поверхность, определяемая этим уравнением есть геометрическое место точек в пространстве, координаты которыхx, y, z удовлетворяют этому уравнению. Это означает, что данному уравнению удовлетворяют координаты x, y, z каждой точки, лежащей на поверхности Q, и не удовлетворяют координаты никакой точки, не лежащей на ней. Уравнение называется уравнением данной поверхностиQ.

1. Общее уравнение плоскости

,

где .

Уравнение плоскости, в котором хотя бы один из коэффициентов А, В, С или D равен нулю, называется неполным уравнением плоскости.

2. Уравнение плоскости, проходящей через точку с данным вектором нормали

Вектором нормали к плоскости называется ненулевой вектор, перпендикулярный к данной плоскости имеет вид:

.

3. Уравнение плоскости в отрезках

,

где - это координаты точек,,, лежащих на координатных осях.

4. Уравнение плоскости, проходящей через три точки ,,

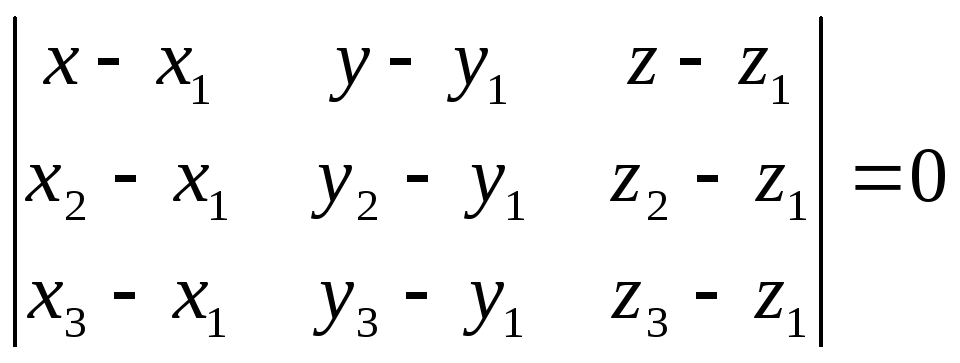
Пример 1. Составить уравнение плоскости, проходящей через три точки ,,.

Решение.

; ;

;

;

;

.

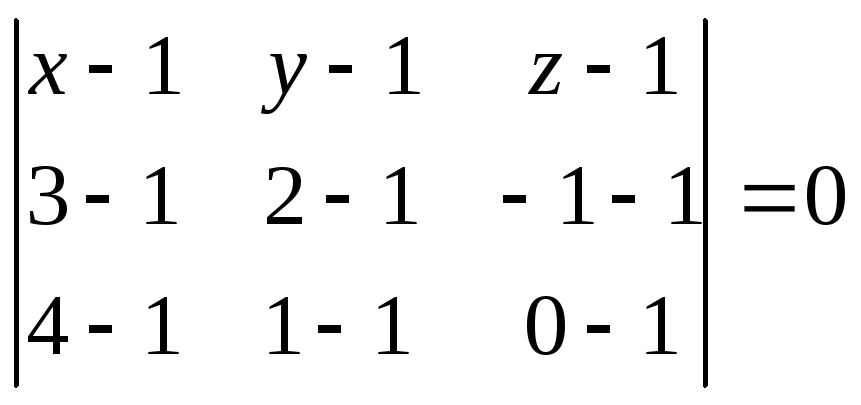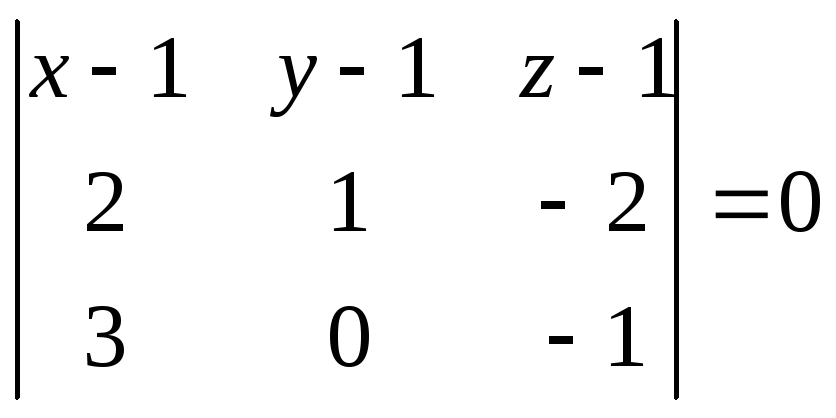Пример 2. Составить уравнение плоскости с нормальным вектором , проходящей через точку.

Решение. ;

;

;

.

Прямая и ее уравнения в пространстве

1. Параметрические уравнения прямой в пространстве

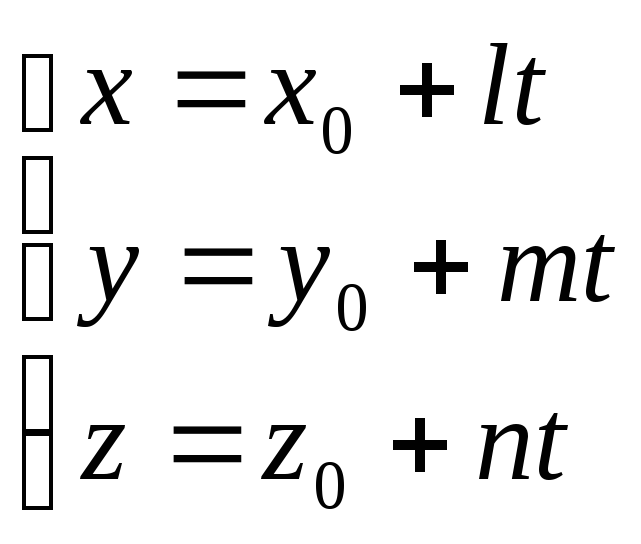
2. Каноническое уравнение прямой в пространстве

.

Вектор - направляющий вектор прямой (вектор, параллельный данной прямой).

3. ,Общее уравнение прямой (прямая как пересечение двух плоскостей)

Рассмотрим две плоскости

;

.

Тогда уравнение прямой как линии пересечения двух плоскостей имеет вид:

.

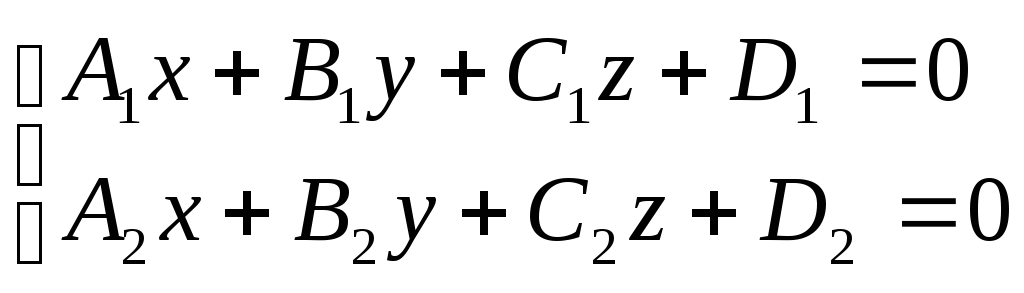Расстояние от точки до прямой

Пусть дана плоскость и точка. Расстояниеот точкидо плоскости вычисляется по формуле:

.

Угол между плоскостями

Углом между двумя плоскостями

;

Считается угол между их нормалями и:

=.

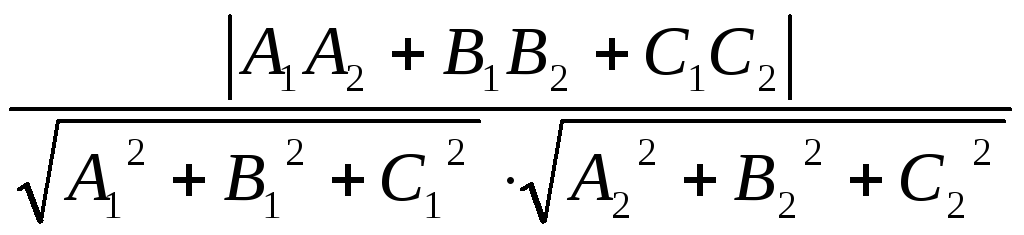Отсюда получим условие перпендикулярности двух плоскостей:

=0.

Условие параллельности двух плоскостей:

.

Угол между двумя прямыми в пространстве

Пусть заданы канонические уравнения двух прямых:

;

Тогда острый угол между прямыми определяется как угол между их направляющими векторами и вычисляется следующим образом:

=.

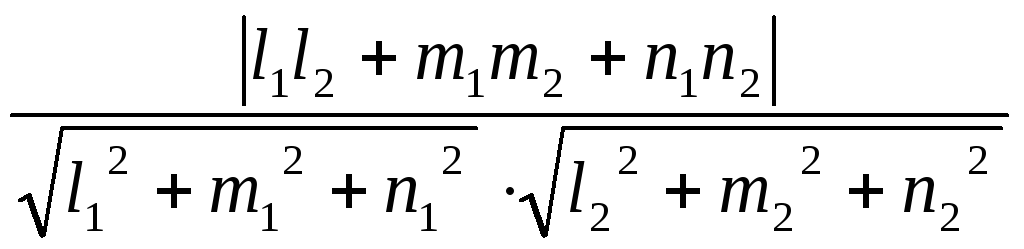Условие перпендикулярности прямых:

=0.

Условие параллельности двух прямых:

.

Угол между прямой и плоскостью

Острый угол между прямой и плоскостью определяется по формуле:

=.

Условие параллельности прямой и плоскости:

=0.

Условие перпендикулярности прямой и плоскости:

.

2.4 Контрольные задания для студентов по разделу 1 «Линейная алгебра» и разделу 2 «Элементы аналитической геометрии»

Задание 1. Найти скалярное произведение

Задание 2. При каком значении векторыивекторы ортогональны?

Задание 3. Найти векторное произведение векторов и?

Задание 4. Являются ли векторы линейно зависимыми?

Задание 5. Вычислить объем треугольной пирамиды, построенной на векторах .

Данные для выполнения заданий 1, 2, 3, 4, 5 необходимо взять из таблицы 1 согласно своему варианту.

Таблица 1

Номер варианта
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

Задание 6. В треугольнике найти уравнение медианы, высоты, проведенных из вершины, а также уравнение средней линии, параллельной основанию. Вычислить длину найденной высоты.

Координаты точек заданы в таблице 2.

Таблица 2

Номер варианта
1	(3,2)	(-2,5)	(6,-2)
2	(-2,6)	(3,-1)	(1,4)
3	(2,5)	(3,3)	(-1,4)
4	(2,-3)	(1,0)	(-2,-4)
5	(5,3)	(1,4)	(-2,-3)
6	(-1,-2)	(0,-3)	(2,1)
7	(1,5)	(-3,0)	(-6,1)
8	(-3,-5)	(2,-2)	(1,0)
9	(1,1)	(4,6)	(-5,-1)
10	(3,2)	(4,-1)	(6,0)
11	(5,-5)	(2,3)	(-4,-3)
12	(1,4)	(2,2)	(-1,6)
13	(2,-3)	(-6,2)	(4,0)
14	(2,6)	(-1,-2)	(-3,-5)
15	(-1,2)	(4,-2)	(6,0)
16	(3,2)	(-2,5)	(-1,4)
17	(-2,6)	(3,-1)	(-2,-4)
18	(2,5)	(3,3)	(-2,-3)
19	(2,-3)	(1,0)	(2,1)
20	(5,3)	(1,4)	(-6,1)
21	(-1,-2)	(0,-3)	(1,0)
22	(1,5)	(-3,0)	(-5,-1)
23	(-3,-5)	(2,-2)	(6,0)
24	(1,1)	(4,6)	(-4,-3)
25	(3,2)	(4,-1)	(-1,6)
26	(5,-5)	(2,3)	(4,0)
27	(1,4)	(2,2)	(-3,-5)
28	(2,-3)	(-6,2)	(6,0)
29	(2,6)	(-1,-2)	(6,-2)
30	(-1,2)	(4,-2)	(1,4)

Задание 7. По каноническому уравнению кривой второго порядка определить тип кривой. Найти координаты фокусов, вершин и центра.

Варианты заданий:

1)

2)

3)

4)

5)

6)

7)

8)

9)

10)

11)

12)

13)

14)

15)

16)

17)

18)

19)

20)

21)

22)

23)

24)

25)

26)

27)

28)

29)

30)

Задание 8. Преобразовать к полярным координатам уравнение линии.

Варианты заданий:

1)

2)

3)

4)

5)

6)

7)

8)

9)

10)

11)

12)

13)

14)

15)

16)

17)

18)

19)

20)

21)

22)

23)

24)

25)

26)

27)

28)

29)

30)

Задание 9. Составить уравнение плоскости, проходящей через точку , перпендикулярно прямой.

Варианты заданий:

1) ,

2) ,

3) ,

4) ,

5) ,

6) ,

7) ,

8) ,

9) ,

10) ,

11) ,

12) ,

13) ,

14) ,

15) ,

16) ,

17) ,

18) ,

19) ,

20) ,

21) ,

22) ,

23) ,

24) ,

25) ,

26) ,

27) ,

28) ,

29) ,

30) ,

Задание 10. Составить уравнение плоскости, проходящей через три точки .

Варианты заданий в таблице 3.

Таблица 3

Номер варианта
1	(2,0,-4)	(2,0,-1)	(0,-1,-1)
2	(0,0,1)	(1,-2,5)	(1,5,0)
3	(2,1,0)	(2,1,-5)	(-1,1,1)
4	(10,-10,-1)	(0,-1,0)	(2,1,-1)
5	(1,1,1)	(1,1,-1)	(-4,-2,2)
6	(0,0,1)	(1,-1,3)	(5,0,-1)
7	(1,-2,-6)	(2,-4,-2)	(1,1,1)
8	(-4,8,1)	(1,-2,1)	(-2,5,1)
9	(1,1,0)	(1,-2,-1)	(-1,3,1)
10	(3,0,-1)	(-1,1,1)	(1,-2,3)
11	(0,-1,-1)	(-1,2,1)	(0,1,4)
12	(1,5,0)	(2,-3,10	(1,2,-1)
13	(-1,1,1)	(0,0,1)	(4,3,2)
14	(2,1,-1)	(0,1,-1)	(1,2,-1)
15	(-4,-2,2)	(-2,2,0)	(1,4,1)
16	(5,0,-1)	(2,1,-1)	(1,2,-1)
17	(1,1,1)	(4,3,1)	(2,0,-1)
18	(-2,5,1)	(0,0,2)	(1,-2,5)
19	(-1,3,1)	(0,0,-2)	(2,1,-5)
20	(1,-2,3)	(1,1,1)	(0,-1,0)
21	(0,1,4)	(3,2,-1)	(1,1,-1)
22	(1,2,-1)	(4,1,0)	(1,-1,3)
23	(4,3,2)	(1,4,3)	(2,-4,-2)
24	(1,2,-1)	(3,0,-1)	(1,-2,1)
25	(1,4,1)	(3,2,-2)	(1,-2,-1)
26	(1,2,-1)	(1,-2,5)	(-1,1,1)
27	(1,2,5)	(3,-6,0)	(-1,2,1)
28	(1,1,1)	(-1,5,2)	(2,-3,10
29	(2,3,0)	(0,3,-4)	(0,0,1)
30	(0,2,0)	(2,2,2)	(0,1,-1)