6.2 Знакочередующиеся числовые ряды. Признак Лейбница

Определение. Числовой ряд, члены которого поочередно имеют то положительные, то отрицательные знаки, называется знакочередующемся рядом и записывается в виде

,

где (ряд может начинаться и с отрицательного члена).

Теорема (признак Лейбница). Если члены знакочередующегося ряда монотонно убывают по абсолютной величине

и стремятся к нулю

,

то знакочередующийся ряд сходится, и сумма его не превосходит первого члена.

Пример. Исследовать на сходимость знакочередующийся ряд

Решение. Сравним члены данного ряда по абсолютной величине

Видим, то члены искомого ряда монотонно убывают по абсолютной величине.

Найдем .

Таким образом, согласно признаку Лейбница, искомый ряд сходится.

Сходимость произвольных рядов

Выясним вопрос о сходимости рядов

,

члены которых могут иметь произвольные знаки.

Теорема (достаточный признак сходимости числового ряда). Пусть дан ряд с членами произвольных знаков. Если сходится ряд

,

составленный из абсолютных величин его членов, то сходится и данный ряд.

Пример. Исследовать сходимость ряда

Решение. Данный ряд является произвольным. Рассмотрим ряд, составленный из абсолютных значений исходного ряда:

(*)

и ряд

(**)

Члены ряда (*) не больше соответствующих членов ряда (**). Ряд (**) сходится, как обобщенный гармонический ряд, следовательно, сходится и ряд (*), а значит и исходный ряд.

Определение. Если числовой ряд сходится вместе с рядом, составленным из абсолютных величин его членов, то говорят, что числовой ряд сходится абсолютно.

Определение. Если числовой ряд сходится, а ряд, составленный из абсолютных величин его членов, то говорят, что числовой ряд сходится условно.

Пример. Определить, как сходится числовой ряд, абсолютно или условно?

Решение. Исследуем исходный ряд на сходимость.

Так как , следовательно, видим, что члены ряда убывают по абсолютной величине. Кроме того,.

Таким образом, согласно признаку Лейбница, искомый ряд сходится.

Рассмотрим ряд, составленный из абсолютных величин данного ряда:

Этот ряд расходится как обобщенный гармонический ряд (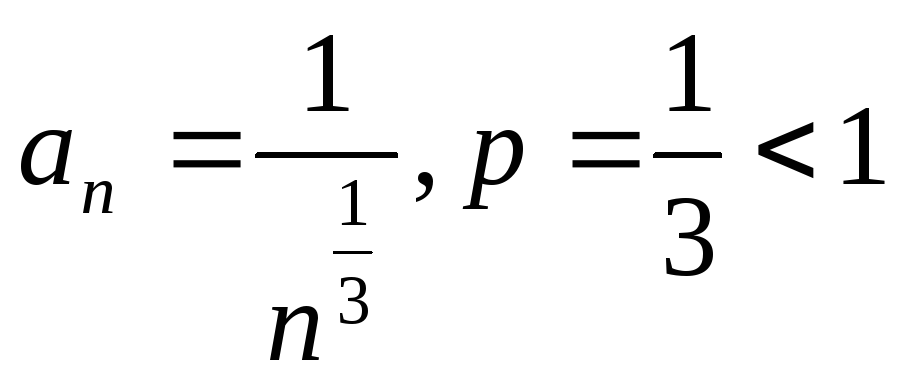). Делаем вывод, что данный ряд сходится условно.

6.3 Степенные ряды

Определение. Ряд

называется функциональным, если члены его являются функциями от переменной х.

Давая переменной х определенные числовые значения, получаем сходящиеся или расходящиеся числовые ряды.

Если в точке рядсходится, то точканазывается точкой сходимости. Если этот ряд расходится, то точка- точка расходимости ряда. Совокупность тех значений х, при которых функциональный ряд сходится, называется областью сходимости этого ряда.

Пример. Ряд сходится в интервале (-1; 1), так как при любомсоответствующий числовой ряд есть геометрический ряд со знаменателемq=x. При этот ряд расходится. Следовательно, область сходимости исходного ряда есть интервал (-1; 1).

Определение. Функциональный ряд называется равномерно сходящимся в област D, если для любого числа можно указать такое число, не зависящее оти не зависящее от, что при всех номерахнеравенствосправедливо для всех точекD (где - остаток ряда).

Теорема (признак Вейерштрасса). Если члены функционального ряда удовлетворяют в области D неравенствам

,

где - члены некоторого сходящегося знакоположительного ряда

,

то функциональный ряд сходится равномерно в D.

Замечание. Ряды, для которых выполняются условия теоремы Вейерштрасса, называются правильно сходящимися.

Степенные ряды

Определение. Ряд

называется степенным рядом.

Это функциональный ряд по степеням , поэтому ряд начинается с члена, который называется свободным членом.

Нас будет интаресовать нахождение области сходимости степенного ряда.

Теорема Абеля.

а) Если степенной ряд сходится в точке , то он сходится, и притом абсолютно, в интервале, т.е. при всех, удовлетворяющих неравенству.

б) Если степенной ряд расходится при , то он расходится при всяком, большем по абсолютной величине, чем, т.е. при.

Кроме того, при исследовании степенных рядов можно воспользоваться одним из признаков сходимости знакоположительных числовых рядов, например, признаком Даламбера.

Совокпность всех , при которых степенной ряд сходится, называется интервалом сходимости ряда. Областью сходимости степенного ряда является интервал, к которому в зависимости от конкретных случаев могут быть добавлены концевые точки.

- радиус сходимости степенного ряда, определяемый по формуле:

.

Замечание. При нахождении интервала сходимости редко пользуются последней формулой, а непосредственно применяют признак Даламбера.

Пример. Найти радиус и интервал сходимости степенного ряда, исследовать поведение ряда на концах интервала сходимости

Решение. Рассмотрим ряд, составленный из абсолютных величин членов ряда ,и применим к нему признак Даламбера

.

Область сходимости данного ряда является решением неравенства .

;

;

.

Следовательно, интервал сходимости есть (-1, 5), а радиус сходимости .

Исследуем поведение ряда на концах интервала:

а) , тогда исходный ряд примет видЭтот ряд расходится, так как не существует конечного пределаn-го члена. Поэтому, точка не является точкой сходимости.

б) , тогда исходный ряд примет видЭтот ряд расходится, так как пределn-го члена равен бесконечности. Поэтому точка не является точкой сходимости.

Итак, интервал сходимости ряда - (-1, 5), а радиус сходимости .