Раздел 5. Математический анализ. Дифференциальные уравнения

5.1 Комплексные числа и действия над ними

Определение. Комплексным числом называется выражение, где- действительные числа, а;называется действительной (вещественной) частью комплексного числа();- мнимая часть комплексного числа().

Два комплексных числа иотличающиеся только знаком мнимой части, называются комплексно сопряженными.

Числа иравны (), еслии.

Для геометрического изображения комплексного числа введем понятие комплексной плоскости. На плоскости ХОУ комплексное число изображается точкой(или вектором); ось ОХ называется действительной осью, а ось ОУ – мнимой.

Действия над комплексными числами

1. Суммой двух комплексных чисел иназывается комплексное число.

2. Разностью двух комплексных чисел иназывается комплексное число.

3. Чтобы найти произведение двух комплексных чисел и, следует перемножить их по обычным правилам алгебры, учитывая, что:

.

Заметим, что произведение двух сопряженных чисел – неотрицательное действительное число:

.

4. Для деления комплексных чисел и() надо домножить числитель и знаменатель на число, сопряженное знаменателю:

Тригонометрическая форма комплексного числа

Обозначим через иполярные координаты точки. Тогдаи- тригонометрическая форма комплексного числа. Числоназывается модулем, а- аргументом комплексного числа:, при этом

, ,,.

Формула Муавра для возведения комплексного числа в степень:

.

Формула корня n-й степени из комплексного числа:

.

5.2 Дифференциальные уравнения первого порядка

Определение. Дифференциальным уравнением (д.у.) называется уравнение, содержащее производные неизвестной функции.

Если неизвестная функция зависит только от одного переменного, то д.у. называется обыкновенным; если от нескольких переменных и производные, входящие в д.у. – частные, то дифференциальным уравнением с частными переменными.

Так как наиболее частным случаем является изучение тех или иных характеристик процессов, протекающих во времени, то независимую переменную в обыкновенном д.у. будем обозначать через t, а функцию через х.

Наивысший порядок производной неизвестной функции, входящей в д.у. называется порядком дифференциального уравнения.

Решением дифференциального уравнения называется функция, при подстановке которой д.у. обращается в тождество.

Общий вид д.у. первого порядка есть

.

Задача Коши для д.у. первого порядка, разрешенного относительно производной:

найти определенную на некотором интервале функцию, имеющую напроизводнуютакую, что

для всех

и удовлетворяющую условию

,

где , а в точкеопределена функция.

Значения ,при этом называются начальными данными, а условие- начальным условием.

Итак, задача Коши для д.у. состоит в нахождении решения д.у., удовлетворяющего заданному начальному условию.

Виды дифференциальных уравнений первого порядка

1. Дифференциальные уравнения с разделенными переменными

Уравнение вида

называется дифференциальным уравнением первого порядка с разделенными переменными.

Пример. Решить дифференциальное уравнение

.

Решение.

;

;

;

;

.

2. Дифференциальные уравнения с разделяющимися переменными

Уравнение вида

называется дифференциальным уравнением первого порядка с разделяющимися переменными.

Разделим обе части д.у. на , получим уравнение

,

которое является уравнением с разделенными переменными.

Пример. Решить дифференциальное уравнение

.

Решение.

Разделим обе части уравнения на , получим

;

;

;

;

;

.

3. Однородные уравнения первого порядка

Уравнение вида

,

где - однородная функция нулевого измерения, называется однородным д.у. первого порядка.

Заменой ,д.у. сводится к уравнению с разделяющимися переменными.

Пример. Решить дифференциальное уравнение

.

Решение.

;

.

Сделаем замену ,, получим

;

.

Разделим обе части уравнения на , получим

;

;

;

;

.

Тогда, .

4. Уравнение Бернулли

Уравнение вида

называется уравнением Бернулли.

Для решения уравнения делают замену

.

Тогда уравнение Бернулли примет вид

;

.

Найдем из решения уравнения,найдем из решения уравнения.

Пример. Решить дифференциальное уравнение

Решение. Сделаем замену , получим

;

.

1) решим уравнение

;

;

;

;

;

2) решим уравнение

;

;

;

;

;

;

;

;

Тогда, .

5. Линейное уравнение первого порядка

Уравнение Бернулли при , т.е. дифференциальное уравнение вида

называется линейным уравнением первого порядка.

Замена и метод решения линейного д.у. первого порядка аналогичны замене и методам решения уравнения Бернулли.

Пример. Решить дифференциальное уравнение

.

Решение. Сделаем замену , получим

;

;

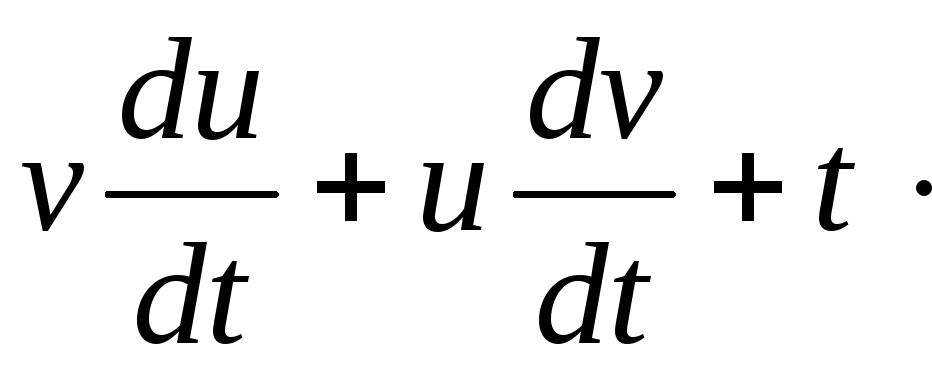
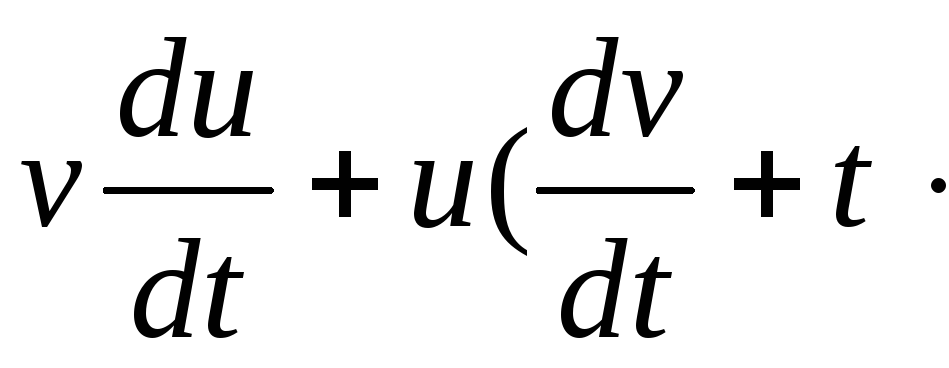
1) Решим уравнение ;

;

;

;

;

2) Решим уравнение ;

;

;

;

;

.

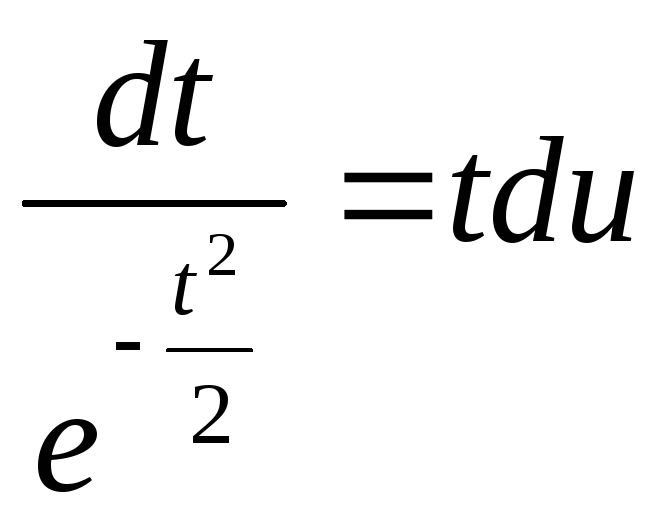Тогда, решением д.у. является функция .